Название | Водоизмещение, т | Длина, м | Ширина, м | Осадка, м | Мощность ЭУ, КВт | Скорость, уз. | Кол-во сейсмокос и их длина |
СGG Alize | 11 500 | 100 | 29 | 7,55 | 2 х 4 200 | 14,5 | 16 х 6000 |
Simphony | 10 000 | 120,7 | 28,4 | 7,2 | 2 х 3690 | 14 х 8000 | |
Ramform | 8380 | 82 | 39,6 | 5,8 | 10 000 | 14 | 12 х 6000 |
Veritas | 8 000 | 93 | 22 | 6,5 | 2 х 4 320 | 15,5 | 8 х 8 000 |
Geo | 7 200 | 91 | 24 | 6,4 | 2 х 3300 | 12 х 8 000 | |
Amadeus | 5 600 | 84 | 18,5 | 6,2 | 2 х 2 500 | 8 х 9 000 | |
Orion | 5 200 | 81 | 18,3 | 5,2 | 2 х 2 700 | 8 х 6 000 | |
Pacific Titan | 3 200 | 64,5 | 18,5 | 5,2 | 4 х 1120 | 2 х 8 000 | |
Пр. В-93 | 3 000 | 83 | 14,8 | 5,2 | 3 090 | 14,5 | 4 х 8 000 |
Пр. 650 | 2 200 | 71,6 | 12,8 | 4,5 | 2 х1100 | 12 | 1 х 6000 |
Рассмотрение производственных процессов ГС и РС, их характеристик позволяет сделать вывод о возможности переоборудования РС в ГС
в случае такой необходимости. При этом очевиден одинаковый подход
к требованиям остойчивости, непотопляемости, тяговым характеристикам ГС и РС, которые в равной степени являются "судами с возом", т. е. судами, буксирующими забортное оборудование (сейсмокомплекс или трал). Это доказывает и рассмотрение характеристик РС и ГС, приведенных в табл. 5.
Таблица 5. Характеристики БМРТ и НИС
Характеристика | Обозначение | БМРТ пр. В-26 | НИС пр. В-93 |
1. Полное водоизмещение, т | D | 3700 | 3300 |
2. Год и место постройки | – | 1970, ПНР | 1985, ПНР |
3. Мощность ГД, кВт | NГД | 1750 | 3000 |
4. Мощность СЭС, КВт | NЭЛ | 3 х 300 | 2 х 550; 1 х 1200 |
5. Скорость судна, узл | V | 12,5 | 14,5 |
6. Длина судна между перпендикулярами, м | L┴┴ | 78 | 73,5 |
7. Ширина судна, м | B | 13,8 | 14,8 |
8. Осадка, м | T | 5,5 | 5,0 |
9.Коэффициент полноты КВЛ | Α | 0,8 | 0,82 |
10. Коэффициент общей полноты | Δ | 0,59 | 0,635 |
11. Коэффициент полноты миделя | Β | 0,96 | 0,967 |
12. Коэффициент вертикальной полноты | Χ | 0,735 | 0,775 |
13. Коэффициент Нормана | αβ/δ | 1,3 | 1,25 |
14. Метацентрическая высота, м | H | 0,5 | 0,69 |
Равнозначность характеристик ГС и РС также подтверждается коэффициентом Нормана. Для современного ГС он составляет 1,25 а для РС упомянутый коэффициент имеет значение 1,3. Отсутствие абсолютного равенства этих коэффициентов объясняется различием в назначении судов и использовании забортного оборудования.
Исследование математического описания системы "судно – забортное оборудование" (С – ЗО) и полученные при этом результаты также свидетельствуют о подобии характеристик РС и ГС. Рассмотрена математическая модель движения судна в системе С – ЗО в трех системах координат: неподвижной декартовой OgXgYgZg ; системе координат, связанной с жидкостью O'gX'gY'gZ'g и системе координат, связанной с судном OXYZ. Положение судна и кинематика его движения в указанных системах координат характеризуется следующими параметрами:
- Xg,, Yg – координаты ЦТ судна в неподвижной системе координат;
- ύ – скорость центра тяжести судна;
- ω – угловая скорость вращения судна;
- β, ψ, q – углы дрейфа, курса и скорости;
- R – мгновенный радиус кривизны траектории ЦТ.
Тогда уравнение движения системы С-ЗО будет:
m (1 + k11)_ύ cos β - m(1 + k11) ύ _β sin β + m(1 + k22) ύ ω sin β = TE – XK – XP – TX
– m(1 + k22) ύ sin β – m(1 + k22) ύ β sin β + m(1 + k11) ύ ω sin β = YK + YB –YP + YA + TY
JZ (1 + k66) ω – m (k22 –k11) ύ2 sin β cos β = MK + MP – MB – MT – MA,
где:
- k11, k22, k66 – коэффициенты присоединенных масс вдоль продольной и поперечной осей судна и присоединенного момента инерции;
- m – масса судна;
- JZ – момент инерции судна относительно вертикальной оси;
- X, YK, MK – продольная и поперечная сила на руле и момент, создаваемый поперечной силой руля относительно ЦТ судна;
- YA, MA – поперечная аэродинамическая сила и момент, создаваемый относительно ЦТ судна;
- YB, MВ – поперечная сила от гребного винта и момент, создаваемый относительно ЦТ судна;
- TE – полезная тяга винта;
- TX, TY – проекция горизонтальной силы на оси X, Y;
- MТ – момент от силы TY.
Результаты исследования математической модели движения судна в системе "С-ЗО" также свидетельствуют о подобии характеристик РС и ГС.
Не менее убедительным в этом отношении является сравнительный анализ математических моделей основных характеристик ГС и РС. Для этой цели в работе разработаны математические модели основных характеристик ГС и РС методом подбора функций по эмпирическим данным.
В результате построены модели зависимости ЗДВ, ЗШВ, ЗОВ, ЗМВ.
ЗДВ ГС представлена математической моделью вида L = a·Db , основные параметры которой (и всех далее приведенных моделей) получены методом наименьших квадратов. Граф – модель ЗДВ ГС приведена на рис. 8.
ЗДВ РС представлена математической моделью вида L = а·Db, ее граф-модель приведена на рис. 9.
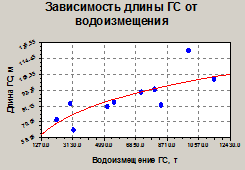
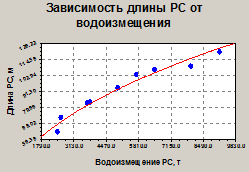
Рис. 8. Зависимость длины ГС | Рис. 9. Зависимость длины РС |
ЗШВ ГС представлена математической моделью вида W = a·Db, ее граф –приведена на рис. 10.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 |





