1. В чем заключается принцип Гюйгенса-Френеля?
2. Какие волны называются когерентными?
3. Что называется дифракцией света? Как объясняется это явление?
4. Каков порядок следования цветов в дифракционных спектрах? Какова окраска нулевого максимума?
5. Чем отличаются дифракционные спектры, даваемые решетками с одинаковым количеством щелей, но с различными постоянными, и решетками с одинаковыми постоянными, но с различным количеством щелей?
6. Как изменится действие дифракционной решетки, если ее поместить в воду?
7. Как объяснить образование дифракционного спектра от одной щели на экране от лучей, прошедших через щель? От чего зависит распределение интенсивности в центре экрана?
8. Одномерная дифракционная решетка. Как объясняется образование дифракционной картины на экране? В каких точках наблюдаются максимумы интенсивности, в каких минимумы и почему?
9. Чем отличаются дифракционные картины при освещении решетки монохроматическим светом и белым светом? Как объяснить эти явления?
10. Что такое интерференция света? Участвует ли это явление при образовании дифракционного спектра на щели или решетке?
11. Белый свет падает нормально на одномерную дифракционную решетку, содержащую 100 щелей на 1 мм. Как распределится интенсивность света на экране? Сколько дополнительных минимумов между двумя главными максимумами образуется на экране? Каковы условия образования главных максимумов и главных минимумов?
12. Белый свет падает нормально на дифракционную решетку и на тонкую линзу большего диаметра. Как объяснить картины, образовавшиеся на экране при прохождении света через линзу и дифракционную решетку?
13. Каковы длины волн видимого света? Подвержены ли они дисперсии?
14. От чего зависит ширина полос дифракционного спектра? Что наблюдается на экране, если ширина щели намного больше длины волны l? Как объясняется это явление?
15. Что называется линейной и угловой дисперсией дифракционной решетки?
16. Что называется разрешающей силой дифракционной решетки?
17. Приведите пример дифракционных картин, получающихся для двух спектральных линий с помощью решеток, отличающихся разрешающей силой и линейной дисперсией.
Лабораторная работа № 4
Исследование вольт-амперных характеристик фотоэлемента
4.1. Цели и задачи работы
Цели работы:
– Ознакомление студентов с изучением законов внешнего фотоэффекта.
Задачи работы:
– Исследование вольт-амперных характеристик фотоэлемента.
– Определение погрешности измерений.
4.2. Теоретическая часть
4.2.1. Фотоэффект
Большое число современных промышленных и лабораторных установок для измерения, контроля и регулирования различных физических и технологических процессов основаны на применении чувствительных к свету элементов – фотоэлементов.
В фотоэлементах используются электрические явления, возникающие в металлах и полупроводниках под действием падающего на их поверхность света. Эти явления носят название фотоэффекта и заключаются в том, что электроны, находящиеся внутри проводника, получают дополнительную энергию от светового потока.
В настоящее время известны три вида фотоэффекта:
1. Внешний фотоэффект, представляет собой фотоэлектронную эмиссию с поверхности металлов.
2. Внутренний фотоэффект, заключающийся в изменении электрического сопротивления некоторых полупроводников под действием света.
3. Вентильный фотоэффект, в результате которого возникает разность потенциалов между слоями двух веществ с различной природой электропроводности.
Соответственно названным трем видам фотоэффекта различают три типа фотоэлементов: фотоэлементы с внешним фотоэффектом, фотосопротивления с внутренним фотоэффектом и вентильные фотоэлементы.
В 1890 году были сформулированы три закона для внешнего фотоэффекта:
1. При фиксированной частоте падающего света число фотоэлектронов, испускаемых фотокатодом в единицу времени, пропорционально интенсивности света (сила фототока насыщения пропорциональна энергетической освещенности катода).
2. Максимальная начальная скорость (максимальная начальная кинетическая энергия) фотоэлектронов не зависит от интенсивности падающего света, а определяется только его частотой n.
3. Для каждого вещества существует красная граница фотоэффекта (зависящая от химической природы вещества и состояния его поверхности) – минимальная частота ![]() света, ниже которой фотоэффект невозможен.
света, ниже которой фотоэффект невозможен.
Для объяснения механизма фотоэффекта Эйнштейн предположил, что свет частотой n не только испускается отдельными квантами (согласно гипотезе Планка), но и распространяется в пространстве и поглощается веществом отдельными порциями (квантами), энергия которых ![]() .
.
Кванты электромагнитного излучения, движущиеся со скоростью света с в вакууме, называются фотонами.
Энергия падающего фотона расходуется на совершение электроном работы выхода ![]() из металла и на сообщение вылетевшему электрону кинетической энергии.
из металла и на сообщение вылетевшему электрону кинетической энергии.
Уравнение Эйнштейна для внешнего фотоэффекта:
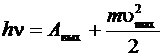 .
.
Это уравнение объясняет зависимость кинетической энергии фотоэлектронов от частоты падающего света. Предельная частота 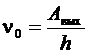 (или длина волны
(или длина волны 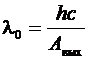 ), при которой кинетическая энергия фотоэлектронов становится равной нулю, и есть красная граница фотоэффекта.
), при которой кинетическая энергия фотоэлектронов становится равной нулю, и есть красная граница фотоэффекта.
Существует и другая форма записи уравнения Эйнштейна для фотоэффекта:
![]() .
.
4.2.2. Фотоэлементы с внешним фотоэффектом
Фотоэлемент с внешним фотоэффектом представляет собой диод, у которого электронная эмиссия с катода возникает под действием падающего на него светового потока.
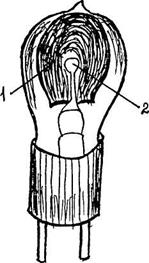
Устройство фотоэлемента показано на рис. 10. В стеклянном герметически закрытом баллоне расположены два электрода – катод 1 и анод 2. Фотокатод выполняется путем нанесения светочувствительного материала на внутренней поверхности стеклянной колбы фотоэлемента так, чтобы светочувствительный слой был обращен внутрь колбы. В качестве светочувствительного материала чаще всего применяется цезий. Анод фотоэлемента выполняется в виде небольшого кольца (или сетки), которое укрепляется на ножке в цоколе. При такой форме анод не мешает лучам света попадать на катод.
|
Рис. 10. Фотоэлемент с внешним фотоэффектом |
Фотоэлементы с внешним фотоэффектом изготавливаются двух типов: вакуумные и газонаполненные. У вакуумных фотоэлементов воздух откачивается до глубокого вакуума. У газонаполненных – после откачки воздуха колба заполняется инертным газом (аргоном, гелием) до давления порядка 0.01 – 1 мм. рт. ст.
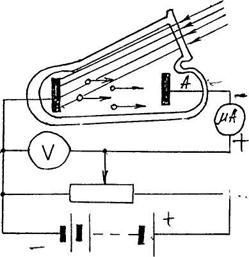
Для исследования зависимости силы фототока от освещенности и напряжения на электродах, собирается схема, показанная на рис. 11. Фотоэлемент показан в удобном для представления виде. Освещенность катода изменяется изменением расстояния между источником света и фотоэлементом. При увеличении расстояния источника света, освещенность изменяется по закону:
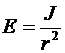 .
.
где J – сила света источника, r – расстояние между источником света и фотоэлементом.
При приближении к источнику освещенность увеличивается по закону:
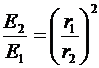 ,
,
откуда для различных значений кратности освещенностей E, 2E, 3E, … расстояние между источником света и фотоэлементом будет равна 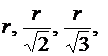 ….
….
|
Рис. 11. Схема установки |
4.3. Приборы и принадлежности:
– Прибор лабораторный – 1 шт.
– Провода – 2 шт.
– Источник питания – 1 шт.
4.4. Порядок выполнения работы
1. Подключить источник питания к прибору. Включить источник питания, прибор и фотоэлемент при помощи переключателей.
2. Установить источник света на расстоянии r от фотоэлемента.
3. Измерить силу фототока, изменяя напряжение от 0 В до 7 В с интервалом 1 В.
4. Повторить п. 3 для расстояний от источника света до фотоэлемента равными 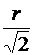 ,
, ![]() и
и ![]() . Результаты измерений занести в таблицу 7.
. Результаты измерений занести в таблицу 7.
5. По числовым данным таблицы построить на одном графике зависимости силы фототока от напряжения при различных освещенностях.
Таблица 7. Вольт-амперные характеристики фотоэлемента
№ | r, см | U, В | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
1 | I, мкА | |||||||||
2 | ||||||||||
3 | ||||||||||
4 |
4.5. Контрольные вопросы
1. Как устроен фотоэлемент с внешним фотоэффектом?
2. Сформулируйте законы фотоэффекта.
3. Что называют током насыщения фотоэлемента?
4. При какой частоте падающего света наблюдается фотоэффект? Что такое красная граница фотоэффекта?
5. Почему с увеличением фотоосвещенности увеличивается фототок при одном и том же напряжении на контактах фотоэлемента?
6. По какому закону увеличивается освещенность фотоэлемента при его приближении к источнику света?
7. Как объясняется увеличение фототока при повышении напряжения на контактах фотоэлемента при неизменном освещении?
8. Изобразите схематично фотоэлемент с внешним фотоэффектом, назовите его элементы и объясните принцип работы
9. По построенной вольт-амперной характеристике фотоэлемента поясните понятие области насыщения.
10. Как зависит выходной ток от освещенности фотоэлемента? Объясните эту зависимость.
11. Как формулируются законы внешнего фотоэффекта?
12. Подтверждаются ли в данной работе законы фотоэффекта?
13. Запишите формулу Эйнштейна для внешнего фотоэффекта и проанализируйте ее. Какие составляющие формулы Эйнштейна подтверждаются выполненной лабораторной работой?
14. Какое напряжение называется зажигающим, от чего оно зависит?
Лабораторная работа № 5
Изучение поляризации света
5.1. Цели и задачи работы
Цели работы:
– Ознакомление студентов с явлением поляризации света.
Задачи работы:
– Определить показатель преломления стекла при помощи угла Брюстера.
– Экспериментально проверить справедливость закона Малюса.
– Определить закономерности при наблюдении двойного лучепреломления на кристалле исландского шпата.
5.2. Теоретическая часть
5.2.1. Поляризация света
Как известно, плоская электромагнитная световая волна является поперечной и представляет собой распространение взаимно перпендикулярных колебаний: вектора напряженности электрического поля ![]() и вектора напряженности магнитного поля
и вектора напряженности магнитного поля ![]() (рис. 12, а). Вектор
(рис. 12, а). Вектор ![]() называется световым вектором, и все преставления о свете можно ограничиться рассмотрением этого вектора. Наличие вектора
называется световым вектором, и все преставления о свете можно ограничиться рассмотрением этого вектора. Наличие вектора ![]() подразумевается.
подразумевается.
Световой пучок, в котором различные направления вектора ![]() в поперечной к направлению распространения волны плоскости равновероятны, называется естественным. В естественном свете колебания различных направлений быстро и беспорядочно сменяют друг друга (рис. 12, б).
в поперечной к направлению распространения волны плоскости равновероятны, называется естественным. В естественном свете колебания различных направлений быстро и беспорядочно сменяют друг друга (рис. 12, б).
Свет, в котором направления колебаний вектора ![]() упорядочены каким-либо образом и подчиняются некоторой закономерности, называется поляризованным. Если колебания вектора
упорядочены каким-либо образом и подчиняются некоторой закономерности, называется поляризованным. Если колебания вектора ![]() могут совершаться лишь в одном определенном направлении, то свет называется линейно или плоскополяризованным (рис. 13, а).
могут совершаться лишь в одном определенном направлении, то свет называется линейно или плоскополяризованным (рис. 13, а).
Если же колебания вектора ![]() совершаются так, что его конец описывает круг или эллипс, то свет называется соответственно поляризованным по кругу или эллиптически поляризованным (рис. 13, б, в). При линейной поляризации плоскость, содержащая луч и вектор
совершаются так, что его конец описывает круг или эллипс, то свет называется соответственно поляризованным по кругу или эллиптически поляризованным (рис. 13, б, в). При линейной поляризации плоскость, содержащая луч и вектор ![]() , называется плоскостью колебаний или плоскостью поляризации волны.
, называется плоскостью колебаний или плоскостью поляризации волны.
Для получения линейно поляризованного света применяются специальные оптические приспособления – поляризаторы. Плоскость колебаний электрического вектора в волне, прошедшей через поляризатор, называется плоскостью поляризатора.
Всякий поляризатор может быть использован для исследования поляризованного света, т. е. в качестве анализатора. В этом случае плоскость колебаний прошедшего света будет совпадать с плоскостью анализатора. Интенсивность I линейно поляризованного света после прохождения через анализатор зависит от угла a, образованного плоскостью колебаний падающего на анализатор луча с плоскостью анализатора, соответственно закону Малюса
![]() ,
,
где ![]() – интенсивность падающего на анализатор света.
– интенсивность падающего на анализатор света.
Для получения плоскополяризованного света существует несколько способов, которые рассмотрены ниже.
5.2.2. Отражение света от поверхности диэлектрика
Отраженный от диэлектрика свет всегда частично поляризован. На рис. 14 черные кружочки соответствуют колебаниям вектора ![]() , перпендикулярным плоскости падения, черточки – колебаниям в плоскости падения. Степень поляризации отраженного луча зависит от относительного показателя преломления и от угла падения i. При падении луча
, перпендикулярным плоскости падения, черточки – колебаниям в плоскости падения. Степень поляризации отраженного луча зависит от относительного показателя преломления и от угла падения i. При падении луча ![]() на плоскость МN под углом Брюстера
на плоскость МN под углом Брюстера ![]() отраженный луч
отраженный луч ![]() полностью поляризован. Преломленный луч
полностью поляризован. Преломленный луч ![]() поляризован частично. Соотношение
поляризован частично. Соотношение
![]()
называется законом Брюстера. Плоскость колебаний электрического вектора в отраженном свете перпендикулярна плоскости падения (рис. 14).
Поскольку отраженный от диэлектрической пластинки свет частично (или даже полностью) поляризован, проходящий свет также частично поляризуется и становится смешанным светом. Преимущественные колебания электрического вектора в прошедшем свете будут совершаться в плоскости падения. Максимальная, но не полная поляризация проходящего света достигается при падении под углом Брюстера. Для увеличения степени поляризации проходящего света используют стопу стеклянных пластинок, расположенных под углом Брюстера к падающему свету. В этом случае можно получить практически полностью поляризованный проходящий свет, так как каждое отражение ослабляет пропущенные колебания, перпендикулярные плоскости падения в определенном отношении.
5.2.3. Преломление света в двояковыпуклых кристаллах
Некоторые кристаллы обладают свойством двойного лучепреломления. Преломляясь в таком кристалле, световой луч разделяется на два линейно поляризованных луча с взаимно перпендикулярными направлениями колебаний. Один из лучей называется обыкновенным и обозначается буквой о, второй — необыкновенным и обозначается буквой е.
Обыкновенный луч удовлетворяет обычному закону преломления и лежит в одной плоскости с падающим лучом и нормалью. Для необыкновенного луча отношение синусов углов падения и преломления не остается постоянным при изменении угла падения. Кроме того, необыкновенный луч, как правило, не лежит в плоскости падения и отклоняется от луча о даже при нормальном падении света.
Отклоняя один из лучей в сторону, можно получить плоскополяризованный луч. Так устроена, например, поляризационная призма Николя (рис. 15). Две естественные грани кристалла исландского шпата срезаются так, чтобы уменьшить угол между поверхностями до 68°. Затем кристалл распиливается на две части по плоскости BD под углом 90° к новым граням. После полировки поверхности распила склеиваются канадским бальзамом, имеющим показатель преломления ![]() удовлетворяющий условию
удовлетворяющий условию ![]() , где
, где ![]() и
и ![]() показатели преломления исландского шпата для обыкновенного и необыкновенного лучей.
показатели преломления исландского шпата для обыкновенного и необыкновенного лучей.
Падая под углом, большим предельного, на плоскость BD, обыкновенный луч претерпевает полное внутреннее отражение на границе шпат-бальзам. Необыкновенный луч, для которого 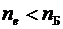 выходит из призмы линейно поляризованным.
выходит из призмы линейно поляризованным.
5.2.4. Поглощение света в дихроических пластинках
У некоторых двоякопреломляющих кристаллов (например, турмалина) коэффициенты поглощения света для двух взаимно перпендикулярных поляризованных лучей отличаются настолько сильно, что уже при небольшой толщине кристалла один из лучей гасится практически полностью и из кристалла выходит линейно поляризованный пучок свега. Это явление называется дихроизмом. В настоящее время дихроические пластинки изготовляют в виде тонких пленок — поляроидов, имеющих широкое применение. В большинстве случаев они состоят из множества маленьких (толщиной до 0,3 мм) параллельно ориентированных кристаллов сернокислого йодистого хинина — герапатита, находящихся внутри связующей среды — прозрачной пленки.
Приборы и принадлежности: Оптическая скамья ФОС-17; люксметр; поворотный столик с круговой шкалой. Поляроид съемный; поляроид встроенный в держателе с круговой шкалой; диапозитив с тремя круглыми кристаллическими пластинами (оптические оси параллельны плоскости пластин); модели из органического стекла; кристалл исландского шпата; щель съемная; стеклянная пластина.
Выполнение работы
Задание1. Экспериментальное подтверждение закона Малюса.
В качестве поляризатора можно взять съемный поляроид, в качестве анализатора - встроенный поляроид с круговой шкалой.
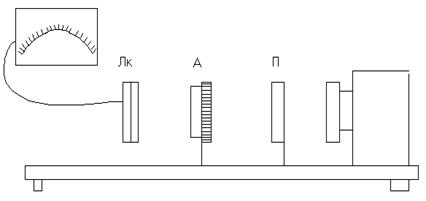
Люксметр (Лк) укрепить на штативе. Установить шкалу анализатора А на нуль и поворотом поляризатора П добиться максимальной освещенности Е. Поворачивая анализатор с шагом ![]() от
от ![]() до
до 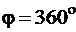 , измерять величину освещенности. Построить график
, измерять величину освещенности. Построить график ![]() и сделать вывод.
и сделать вывод.
Задание 2. а) Интерференция линейно-поляризованного света.
К–диапозитив с тремя круглыми кристаллическими пластинами.
Выяснить, как изменяются цвета при повороте анализатора на 90°, 180°, 270° и 360° (проследить за изменением нескольких цветов). Используя плакат «Цвет света», сделать выводы.
б) Применение фотоупругого эффекта для исследования распределения напряжения в изотропных прозрачных твердых телах.
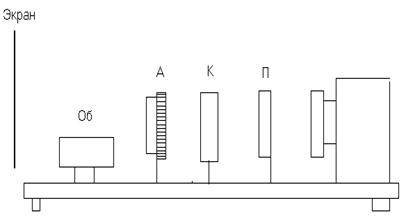
Теперь вместо диапозитива с кристаллическими пластинами устанавливаются модели №1 (балка) и №2 (пластина). До установки моделей на пути световых лучей нужно поляризатор и анализатор установить на полное гашение света (плоскости пропускания П-П и А-А перпендикулярны). Закрепить в держателе модель 1 (с предварительно ослабленным зажимным винтом) и получить ее изображение на экране. Затем зажать модель винтом и проследить за изменениями в изображении на экране. Модель №2 (в держателе не закрепится) испытывается на изгиб аналогичным образом. Сделать необходимые рисунки и выводы по заданию.
Задание 3. Исследование явления двойного лучепреломления.
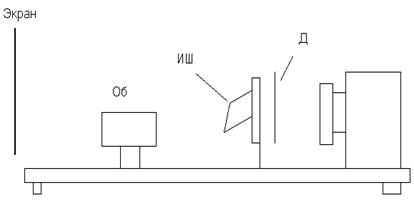
В держателе с диском Д револьверного типа, имеющем круглые диафрагмы различных радиусов, закрепить кристалл исландского шпата ИШ. Установить диафрагму с наименьшим радиусом (≈0,5 мм). Объектив поставить как можно правее (по рисунку) и, перемещая держатель с ИШ, получить четкое изображение на экране. Затем, удерживая рукой держатель с ИШ (чтобы изображение на экране не «дергалось»), плавно вращать окошко с ИШ. Сделать вывод.
Поставить между объективом и кристаллом анализатор с круговой шкалой. Вращая анализатор, следить за изменением характера изображения на экране. Отметив необходимые углы, сделать вывод.
Задание 4. Исследование поляризации при отражении.
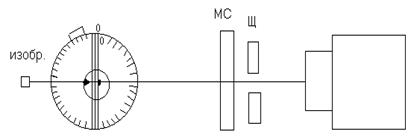
Установить плоскопараллельную стеклянную пластину на поворотном столике. Шкалу столика установить на нуль. Закрепить в одном из держателей съемную щель и с помощью имеющейся на щели пружины установить матовое стекло.
Теперь необходимо добиться, чтобы поверхность стеклянной пластины была перпендикулярна световому пучку (угол падения лучей тогда будет равен нулю). Для этого, глядя сверху со стороны щели и поворачивая предметный столик (не шкалу!) нужно добиться, чтобы щель, центр столика и изображение щели лежали на одной прямой. Затем, поворачивая пластину (не столик!) по часовой стрелке, исследовать отраженный свет на линейную поляризованность с помощью съемного поляроида (при этом глаз, центр столика и изображение щели должны быть на одной прямой!). При достижении некоторого предельного угла Х отраженный свет будет почти полностью гаситься поляроидом. Записать это значение угла. Сняв стеклянную пластину с поворотного столика, определите ее показатель преломления n. После этого нужно сопоставить ![]() с показателем преломления n и сделать выводы.
с показателем преломления n и сделать выводы.
Контрольные вопросы
Какой свет называется поляризованным?
Выведите и объясните закон Малюса.
В чем состоит явление двойного лучепреломления?
Пластинки в полволны и в четверть волны.
Принцип действия призмы Николя.
Интерференция линейно поляризованных лучей.
Получить и проанализировать формулы Френеля.
Как Вы наблюдали внутреннее напряжение при растяжении и сжатии твердых тел? Как оно проявилось?
В чем заключается явление двойного лучепреломления, в каких веществах оно существует, как Вы наблюдали двойное лучепреломление в работе?
Что Вы наблюдали, когда поворачивали образец с многослойными кругами пленок, укрепленной между поляроидами? Объяснить свои наблюдения.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 |