Статистическая функция распределения F*(x) рассчитывается по формуле:

F*(x) =

где - число вариантов вариационного ряда (значений с учетом кратности, т. е. количества повторений), расположенных левее x (включая точку x) , n – объем выборки.

Строим график оценки функции распределения, который представлен на рис.7.

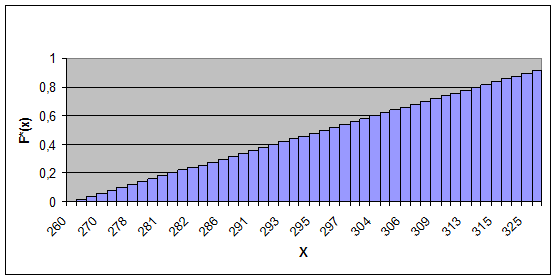
Рис.7. Статистическая функция распределения

Данные для построения статистической функции распределения приведены в приложении 4 (Критерий Колмогорова).

2. Кумулятивная ломаная

Кумулятивную ломаную (вторую оценку функции распределения) строим по формулам:

F** (x ) = 0,

F** (x ) = p,

F** (x ) = p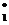 + p,

……………………

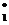F** (x ) = p + p+ … + p ,

где =1.

Результаты расчетов для построения кумулятивной ломаной из таблицы приложения 2 занесем в табл.8.

Таблица 8

Номер интервала

1

2

3

4

5

6

7

Границы интервалов

260;

270,14

270,14; 280,28

280,28; 290,42

290,42; 300,57

300,57; 310,71

310,71;

320,85

320,85;

331

Относительная частота интервалов

0,08

0,1

0,18

0,24

0,16

0,12

0,12

F**(x)

0,08

0,18

0,36

0,6

0,76

0,88

1

График кумулятивной ломаной представлен на рис.8.

Рис.8.Кумулятивная ломаная

4.2.1.6. Статистические оценки плотности распределения

1.  Гистограмма

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат интервалы длиною 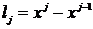, а высота равна отношению = (плотность относительной частоты). Площадь гистограммы относительных частот равна сумме всех относительных частот, т. е. единице.

Учитывая свойство плотности распределения можно записать:

P(xj-1 X<xj )= f(j)*lj, (j=0,q) , где lj – длина j-го интервала, f(j)- средняя на интервале lj плотность распределения f(x).

Заменяя P(xj X<xj+1 ) частотой p*j статистического ряда, получим следующее выражение для приближенного значения f*j плотности распределения на разряде Ij :

f*j= p*j/ lj, j=1,q.

Таким образом, гистограмма относительных частот строится следующим образом: на оси Оx отложим длины разрядов и на них, как на основаниях, построим прямоугольники, имеющие площадь p*j и высоту равную f*j (см. рис.3).

Используем данные из табл. 3. “Статистический ряд” для построения оценок плотности распределения f(x).

Первый способ построения гистограммы: на основе относительных частот. Для построения статистических оценок плотности распределения используем таблицу статистического ряда (табл. 3).

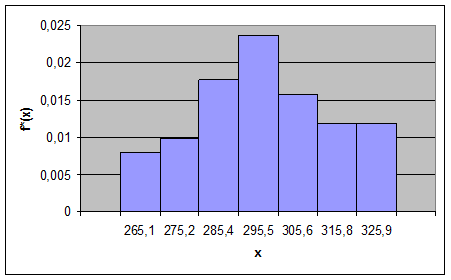
Рис.9. Гистограмма

Существует еще один способ построения гистограммы. Аналогично первому способу отложим на оси ОХ разряды (границы интервалов) из таблицы статистического ряда и на каждом i-ом интервале построим прямоугольник высотой yi: yi=nj. Данная гистограмма приведена на рис.10.

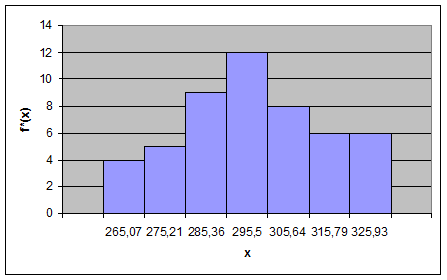
Рис.10. Оценка плотности распределения, построенная по частотам nj.

Данные для построения плотности распределения приведены в Приложении 2 (Интервальная таблица).

2.  Полигон частот

Построим полигон частот – вторую оценку плотности распределения f(x). Полигон относительных частот строится по точкам (, ) , j= (рис. 11)

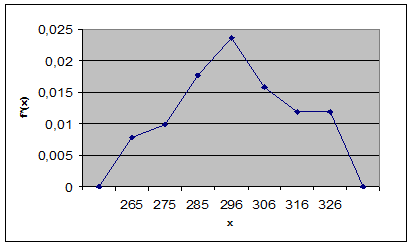
Рис.11. Полигон относительных частот

Полигон частот строим по точкам, координаты которых равны (, nj) , j= (см. рис. 12).

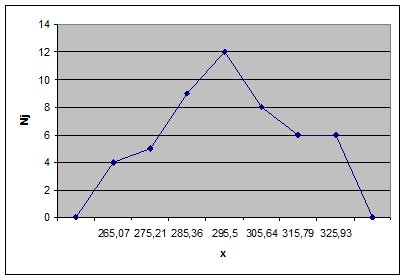
Рис.12. Полигон частот

4.2.2. Проверка статистических гипотез о законе распределения СВ

4.2.2.1. Критерий согласия χ2 Пирсона

В качестве оценок параметров нормального закона примем точечные оценки для математического ожидания и дисперсии:

=296,6 , =331,0612.

Алгоритм проверки гипотезы:

1.  Провести измерения X и получить выборку xn;

2.  Построить вариационный ряд;

3.  Исключить грубые ошибки;

4.  Определить число интервалов ;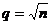

5.  Определить границы интервалов;

6.  Определить количество элементов попадающих в интервал;

7.  Задать гипотезу о плотности распределения f0 (x);

8.Определить вероятность попадания случайной величины в полуинтервал

(xj-1; xj), равную p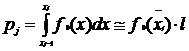j: j,

где - середина lj,

lj– длина интервала.

9.Рассчитать значение реализации статистики проверки гипотезы:

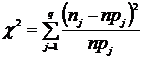, где q –количество интервалов;

10.Задать уровень значимости α;

11.С помощью таблиц распределения Пирсона, по входам α и k=q-r-1 определить, здесь r – количество параметров предполагаемого закона распределения;

12.Принять или отклонить гипотезу по правилу:

если <, гипотеза принимается

если >, гипотеза отклоняется

Расчет значения функции f0(x) будем проводить по формуле:

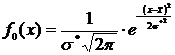, используя при этом встроенную функцию MS Excel НОРМРАСП, параметры которой соответственно равны значению , точечной оценке математического ожидания , точечной оценке среднеквадратического отклонения , четвертый параметр равен 0, что соответствует возвращению функцией значения плотности распределения нормального закона распределения.

Зададим вероятность, а=0,05 практически невозможного события, заключающегося в том, что сумма относительных отклонений оценки плотности распределения от значения функции плотности распределения, принятой в качестве гипотезы, не превзойдет значения 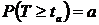. Если выполняется условие: <, то гипотеза принимается.

Значение параметра , возьмем из таблицы распределения 2 Пирсона, исходя из значений вероятности a и числа степеней свободы k=q-r-1, где r- количество параметров предполагаемого закона распределения.

После расчета реализации статистики проверки статистической гипотезы о нормальном распределении (наблюдаемого значения критерия), получили набл=2,2917, которое не превышает значение параметра =9,487728. Следовательно, гипотеза о нормальном распределении случайной выборки принимается.

Результаты расчетов приведены в Приложении 5.

4.2.2.2. Критерий согласия Колмогорова

Критерий Колмогорова позволяет проверить гипотезу о виде функции распределения случайной величины и ее параметрах. Выдвинем следующую гипотезу: случайная величина распределена по нормальному закону с параметрами:

* =296,6 и =18,19509.

В качестве значений параметров берем рассчитанные ранее значения реализаций точечных оценок этих параметров.

Рассчитаем значение реализации статистики проверки гипотезы t:

,

где xi –элемент выборки, .

Расчет значения функции F0(x) можно осуществлять по формуле:

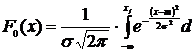x, используя при этом встроенную функцию MS Excel НОРМРАСП, параметры которой соответственно равны значению xi, точечной оценке математического ожидания , точечной оценке среднеквадратического отклонения , значение четвертого параметра равно 1, что соответствует возвращению встроенной функцией значения функции распределения нормального закона.

Алгоритм проверки гипотезы:

1.  Провести измерения Х и получить выборку хn;

2.  Построить вариационный ряд;

3.  Исключить грубые ошибки;

4.  Построить статистическую функцию распределения;

5.  Задать гипотезу, что F0(x) есть функция распределения Х;

6.  Подсчитать t, при этом для вычисления значений функции распределения F0(x) требуется нормализовать выборку значений случайной величины Х, т. е. перейти к случайной величине Y, которая является нормированной случайной величиной Х: yi=(xi-)/ S.;

7.  Задать а и с помощью таблицы Колмогорова найти tα;

8.  Принять или отклонить гипотезу;

Зададим вероятность а=0,05 практически невозможного события, заключающегося в том, что оценка функции распределения отклонится от значения функции принятой в качестве гипотезы, на величину большую, чем tα P(.

Если выполняется условие: t<tα, то гипотеза принимается.

Значение параметра tα возьмем из таблицы Колмогорова, исходя из значений вероятности а и объема выборки n: tα=0,18841.

После выполнения алгоритма проверки гипотезы получили t=0,058, которое не превышает значение параметра tα. Следовательно, гипотеза о нормальном распределении случайной выборки принимается.

Результаты расчетов приведены в Приложении 4.

Выводы

В результате выполненных расчетов было установлено следующее:

1.  При проведении опыта не было выявлено грубых ошибок измерения.

2.  Точечные оценки математического ожидания и дисперсии соответственно равны:

=296,6;

=331,0612;

3. В результате проведенной проверки соответствия закона распределения случайной величины – времени работы программы дефрагментации диска – нормальному закону, было установлено, что с вероятностью = 0,95 практически достоверного события выборочные данные согласуются с гипотезой о нормальном законе распределения исследуемой случайной величины.

Список литературы

1.  Гмурман к решению задач по теории вероятностей и математической статистике: Учеб. пособие для студентов вузов. Изд. 6-е, стер. – М.: Высш. шк., 2001.

2.  Гмурман вероятностей и математическая статистика: Учеб. пособие для вузов.-8-е изд., стер.- М.: Машиностроение, 2002.

3.  , Медведев статистика: Учеб. пособие для втузов.- М.: Высш. шк., 1984.

4.  Кожевников вероятностей и математическая статистика: Учебное пособие для вузов. М.: Машиностроение, 2002.

5.  «Введение в математическую статистику» КГТУ им. , 1996.

6.  Роднищев теории вероятностей и математической статистики: Учебное пособие. Казань: Изд-во Казан. гос. техн. ун-та, 2001.

7.  , «Таблицы математической статистики». М: Наука,1983.

Приложения

Приложение 1. Исключение грубых ошибок

A

B

C

D

E

F

№

Xi

Xi

1

260

295

1339,56

2,56

2

263

296

1128,96

0,36

3

263

297

1128,96

0,16

4

270

298

707,56

1,96

5

272

300

605,16

11,56

6

275

304

466,56

54,76

7

278

305

345,96

70,56

8

279

305

309,76

70,56

9

280

306

275,56

88,36

10

281

307

243,36

108,16

11

281

308

243,36

129,96

12

281

309

243,36

153,76

13

282

310

213,16

179,56

14

283

311

184,96

207,36

15

283

313

184,96

268,96

16

286

314

112,36

302,76

17

287

315

92,16

338,56

18

290

315

43,56

338,56

19

291

320

31,36

547,56

20

291

321

31,36

595,36

21

292

325

21,16

806,56

22

293

326

12,96

864,36

23

294

326

6,76

864,36

24

294

329

6,76

1049,76

25

295

331

2,56

1183,36

СТЕПЕНЬ(A1-296,6;2)

СТЕПЕНЬ(В1-296,6;2)

Xср=

296,6

ta(при а=0,05) =

2,987

S=

18,19509

Xmin=

260

Xmax=

331

Xmin>Xср-Sta

260>242,25127 Xmin не является грубой ошибкой

Xmax<Xср+Sta

331<350,94873 Xmax - не является грубой ошибкой

Приложение 2. Интервальная таблица

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14