Полученная выборка представлена в табл.3.

Таблица 3

2. Краткие теоретические сведения, необходимые для выполнения расчетно-графической работы

2.1. Описание первичной статистической обработки измерений случайной величины

2.1.1. Математическое моделирование простейших измерений. Выборка измерений.

Пусть измеряется некоторая постоянная величина V:

Здесь – результат измерения; D – ошибка измерения; V – измеряемая константа.

(В качестве примера измеряемой константы можно взять длину парты, ширину или высоту двери и т. п.).

По принципу вероятности принимаем, что D – случайная величина с каким-то своим определенным законом распределения, следовательно, из теории вероятностей получаем, что и – случайная величина.

Напомним, что случайная величина (СВ) – это переменная величина, значения которой в опыте случайны, т. е., в результате опыта СВ может принимать одно из некоторого множества возможных значений, образующих полную группу несовместных событий, причем неизвестно заранее, какое именно.

Пусть V измеряется многократно (n раз). Тогда получим ряд результатов измерений (n результатов):

x1=V+d1 – конкретный результат первого измерения (d1 – конкретная ошибка, допущенная при первом измерении);

x2=V+d2 –конкретный результат второго измерения (d2 – конкретная ошибка второго измерения);

…

xn=V+dn – конкретный результат n-го измерения (dn – конкретная ошибка n-го измерения; x1, x2, …,xn, d1, d2, …, dn – конкретные числа).

Полученная в первом измерении ошибка d1- это случайный результат, т. е. d1 можно считать реализацией случайной величины D1, описывающей все возможные ошибки первого измерения.

Следовательно, все возможные результаты первого измерения описываются случайной величиной: X1=V+D1.

Все возможные результаты второго измерения описываются случайной величиной: X2=V+D2, где D2 – случайная величина, описывающая все возможные ошибки второго измерения и т. д.

Все возможные результаты n-го измерения: Xn=V+Dn.

Совокупность всех возможных результатов измерений, таким образом, описывает вектор Xn со случайными компонентами: X1, X2, …, Xn:

Xn=(X1, X2,…, Xn).

Этот n-мерный случайный вектор называется случайной выборкой измерений.

Конкретные результаты n-кратного измерения записывают в виде вектора:

xn=(x1, x2, …,xn),

который является реализацией случайной выборки и называется выборкой измерений.

Из описания этого эксперимента следует, что Xn можно считать случайным результатом конкретных измерений случайной величины X, причём Xi (i=) можно считать i-м экземпляром случайной величины X (состояние СВ Х в i-ом измерении).

Таблица, в которую записываются результаты конкретных измерений СВ Х, называется простым статистическим рядом или простой статистической совокупностью.

Простой статистический ряд имеет вид:

На основе простого статистического ряда или на основе выборки измерений можно решить следующие простые задачи математической статистики:

1)  построить оценку параметра V и исследовать поведение этой оценки в зависимости от Xn, т. е. с учетом всех потенциально возможных значений xi, (i=);

2)  построить оценки:

– функции распределения СВ Х: F(x)=P(X<x),

– плотности распределения СВ Х: f(x)=dF(x)/dx;

3)  построить оценки неизвестных моментов СВ Х: α1=M[X], μ1=M[X–α1] и т. д. в зависимости от Xn и xn.

Таким образом, реализация xn=(x1,…,xn) случайной выборки xn=(x1,…,xn), т. е. простой статистический ряд, служит исходным материалом для статистической обработки результатов измерений.

2.1.2. Построение вариационного ряда

На практике вариационный ряд представляет собой неубывающую последовательность вариантов (x(1),…,x(n)) – последовательность элементов выборки измерений, расположенных в порядке неубывания.

Первый элемент выборки x(1) будем называть минимальным и обозначать его xmin, последний элемент выборки x(n) будем называть максимальным и обозначать xmax. Разность между максимальным и минимальным элементами выборки xmax - xmin называют размахом выборки и обозначают r.

2.1.3. Исключение грубых ошибок измерений

Ошибка измерения – это результат измерения, не соответствующий закону распределения СВ.

Грубые ошибки могут возникнуть вследствие неправильной методики измерения, заведомо ложной, либо с нарушением условий измерений, либо с нарушением условий проведения опытов.

Таким образом, следует убедиться, что реализация xn=(x1,…,xn) выборки xn=(x1,…,xn) действительно соответствует функции распределения F(x). В процессе измерений предполагаемая статистическая обстановка может нарушиться и в связи с этим среди реализаций x1,…,xn могут появиться ошибочные, т. е. не соответствующие функции распределения F(x) значения. Обычно в качестве грубых ошибок подразумевают xmin и xmax и называют их грубыми ошибками, если установлено их несоответствие закону F(x).

Исключение грубых ошибок можно проводить по двум методам: приближенному (логическому) и точному счетному.

Приближенный метод

Согласно этому методу грубые ошибки измерения исключаются по признаку сильного различия от других результатов измерения.

Вычисляем расстояние l=x(n-1)-x(2). Затем сравниваем расстояние между последним (максимальным) элементом и предпоследним x(n-1) с вычисленным расстоянием l:

если (x(n) - x(n-1)) < l, то x(n) – не является грубой ошибкой,

если (x(n) - x(n-1)) l, то x(n) – грубая ошибка.

Аналогично проводится проверка на грубую ошибку первого (минимального) элемента вариационного ряда:

если (x(2) - x(1)) < l, то x(1) – не является грубой ошибкой,

если (x(2) - x(1)) l, то x(1) – грубая ошибка.

Точный счетный метод

Введем случайную величину 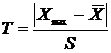– статистику проверки статистической гипотезы о том, что реализация Xmax является грубой ошибкой. Здесь S – точечная оценка стандартного отклонения.

Реализация статистики T имеет вид: .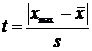

Зададим α - уровень значимости критерия проверки гипотезы о грубой ошибке, т. е. вероятность практически невозможного события

P(t ta)= α), (1)

здесь t – реализация статистики проверки гипотезы.

Далее находим критическую точку ta. из таблицы приложения 11 по входам: объем выборки n и уровень значимости α. Например, исходя из объема выборки n = 50 и вероятности α = 0,05, выберем значение ta=2,987.

Найдем статистическое среднее (выборочное среднее): и реализацию точечной оценки стандартного отклонения: .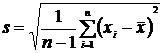

Сравним x*min = - sta c xmin, если xmin > -sta, следовательно, хmin не является грубой ошибкой.

Сравним x*max = + sta с xmax, если xmax < +sta, следовательно, xmax не является грубой ошибкой.

Верхней границей допустимых значений xmax в силу уравнения (1) становится величина x*max = + sta,.

В итоге получаем:

если xmax >= + sta , то xmax является грубой ошибкой и исключается из выборки.

Анализ ошибочности xmin выполняется аналогично: если xmin <= - sta, то xmin является грубой ошибкой и также исключается из выборки.

2.1.4. Построение статистических оценок математического ожидания и дисперсии

Построение точечных оценок

Математическим ожиданием M[X] дискретной случайной величины X называется сумма произведений всех возможных значений случайной величины на вероятности этих значений:

M[X] =

Дисперсией случайной величины называется математическое ожидание квадрата соответствующей центрированной случайной величины:

D[X] = M[(X- M[X])] = p.

Статистической оценкой а* неизвестного параметра а теоретического распределения называют функцию от случайной выборки g(X1, X2, …, Xn).

Точечной оценкой неизвестного параметра а называют статистическую оценку, реализация которой определяется одним числом a*= g(x1, x2, …, xn), где x1, x2, …, xn – выборка измерений, т. е. результаты n измерений случайной величины Х.

Реализация точечной оценки математического ожидания:

.

Для дисперсии реализацией точечной оценки служит выборочная дисперсия

=

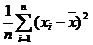
и исправленная выборочная дисперсия

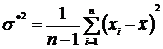
Выборочная дисперсия характеризует рассеяние наблюдаемых значений выборки около среднего значения .

Построение интервальных оценок

Интервальной называют оценку, которая определяется как интервал с двумя концами (в общем случае случайными), покрывающего оцениваемый параметр.

Доверительным называется интервал со случайными концами, который с доверительной вероятностью (надежностью) β содержит (или покрывает) оцениваемый параметр. Поскольку концы интервала представляют собой случайные величины, то их называют доверительными границами.

Интервальная оценка математического ожидания:

)

Для нахождения интервальной оценки математического ожидания необходимо вычислить реализацию точечной оценки среднего квадратического отклонения (реализацию стандартного отклонения):

.

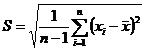Из таблиц распределения Стьюдента по значениям n и a находим значение ta, как решение уравнения:

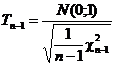
- вероятность практически достоверного события

- граница практически достоверных значений дроби Стьюдента Tn-1

Границы доверительного интервала для :

=

=

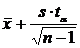
Реализация доверительного интервала для математического ожидания имеет вид:

Интервальная оценка дисперсии

Интервальной оценкой дисперсии служит интервал ID = (1, 2),

где 1 = (nx)/t2, 2 = (nx)/t1 t1, t2 находят из таблиц c2-распределения по входам a 1, a 2 и числу степеней свободы k=n-1.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14