Теория вероятностей и математическая статистика (стр. 4 )

В соответствии с номером варианта объем выборки n = 50, уровень значимости α = 0,05.

4.2. Выполнение расчетно-графической работы

4.2.1. Первичная обработка результатов измерений

4.2.1.1. Построение вариационного ряда

Строим вариационный ряд, т. е. упорядочиваем элементы выборки x1,…,xn в порядке неубывания. Полученный вариационный ряд представлен в табл.6 "Вариационный ряд ".

Вариационный ряд

Таблица 6

4.2.1.2. Исключение грубых ошибок измерений

Выполним проверку выборки измерений на наличие грубых ошибок измерений. Для этого:

1. На основе данных об уровне значимости α =0,05 и начальном объеме выборки n=50 из таблицы Приложения 11 по входам n и α выбираем значение tα=2,987.

2. Определим значения минимального и максимального элементов выборки, подлежащие проверке:

x(1) =xmin =260,

x(n) = xmax = 331.

3. Находим выборочное среднее: = =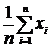296,6.

4. Находим значение параметра s: s =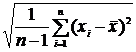 = 18,19509.

5. Выполняем проверку минимального элемента вариационного ряда на грубую ошибку. Сравним -stα=242,25127 c xmin=260, xmin>-stα ,следовательно, хmin=260 не является грубой ошибкой.

6. Выполняем проверку максимального элемента вариационного ряда на грубую ошибку. Сравним +stα =350,94873 с xmax=331, xmax< +stα, следовательно, xmax=331 не является грубой ошибкой и остаётся в выборке.

Расчеты по данному алгоритму приведены в Приложении 1.

Таким образом, грубых ошибок в выборке нет. Заканчиваем их поиск.

После выполнения алгоритма выявления грубых ошибок объем выборки остался прежним: n=50. Соответственно, не изменились и s.

4.2.1.3. Построение статистических оценок математического ожидания и дисперсии

Точечные оценки

Рассчитаем реализацию точечной оценки математического ожидания (выборочное среднее):

= =296,6 с.

Рассчитаем реализацию точечной оценки дисперсии (исправленную выборочную дисперсию):

= = 331,0612 с2.

Интервальные оценки

Доверительная вероятность, с которой доверительный интервал накроет истинное значение параметра закона распределения случайной величины:

=1 – α = 0,95.

Рассчитаем границы доверительного интервала для математического ожидания.

Реализация точечной оценки математического ожидания известна (рассчитана в предыдущем пункте).

Из таблиц распределения Стьюдента по значениям k=(n-1) и находим значение :

=2,.

Границы доверительного интервала для математического ожидания :

= = 291,3

= = 301,8208441.

Полученный доверительный интервал для математического ожидания:

= (291,3791559; 301,8208441) .

Рассчитаем границы доверительного интервала для дисперсии.

Рассчитаем значения:

= 0,025 , 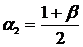= 0,975.

Из таблицы - распределения, по входам k=(n –1)=49 и =0,025, k=(n –1)=49 и =0,975 найдем значения критических точек и :

=32,

= 71,42019.

Границы доверительного интервала рассчитаем по формулам:

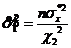= 231,770053 ,

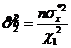= 511,5698078 .

Полученный доверительный интервал для дисперсии:

= (231,770053; 511,5698078).

4.2.1.4. Построение статистического ряда

Находим размах выборки:

r =хmax - xmin=331–260=71.

Находим количество разрядов (интервалов) q=7, длину интервала делаем одинаковой:

li = r/q = 71/ 7 =10,14.

Выделяем представителей разрядов и подсчитываем число элементов выборки nj, попавших в j-й разряд (интервал). Рассчитываем относительную частоту попадания элементов в разряды, т. е. относительные частоты разрядов pj* статистического ряда:

pj* = nj / n , (j=).

На основе относительных частот рассчитываем плотность относительной частоты для каждого разряда по формуле:

= , (j=),

здесь – длина j-го разряда.

Результаты расчетов, приведенные в приложении 3 «Статистический ряд», сводим в таблицу 7.

Статистический ряд

Таблица 7

Номер интервала	1	2	3	4	5	6	7
Границы интервалов	260; 270,14	270,14; 280,28	280,28; 290,42	290,42 ; 300,57	300,57; 310,71	310,71; 320,85	320,85; 331
Длина интервала	10,14	10,14	10,14	10,14	10,14	10,14	10,14
Частота интервала	4	5	9	12	8	6	6
Относительная частота интервалов	0,08	0,1	0,18	0,24	0,16	0,12	0,12
Плотность относительной частоты =	0,00788	0,00985	0,01774	0,02366	0,01577	0,01183	0,01183
Середина интервала	265,07	275,21	285,35	295,5	305,64	315,78	325,92

4.2.1.5. Построение статистических оценок функции распределения

1. Статистическая функция распределения

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14