Вероятности a 1 и a 2 вычисляют по формулам:
a 1=(1+b)/2,
a 2=(1-b)/2.
Здесь b – доверительная вероятность, a = 1–b
Таким образом, интервальная оценка дисперсии – это случайный интервал вида:
(
, 
).
Реализация интервальной оценки дисперсии – это интервал
(
, 
).
2.1.5. Построение статистического ряда
Для построения статистического ряда определяют отрезок числовой оси, содержащий все элементы выборки xn=(x1,…,xn), т. е. интервал (xmin, хmax). Затем необходимо провести группировку выборки на группы, т. е. интервал (xmin, хmax) разбить на полуинтервалы (разряды). Для этого необходимо разделить точками х1,х2,…,хq действительную ось на q непересекающихся полуинтервалов (хj, хj+1), j=
, одинаковой длины.
Количество разрядов вычисляем по формуле: q=
, q=5-20, а длину разряда вычисляем по формуле:
l = (хmax – xmin.)/q
Причем xmin = х1, хmax = хq.
После этого для каждого из разрядов находят представителей разрядов, т. е. устанавливают координаты средних точек разрядов 
. Затем находят число элементов выборки nj, попавших в разряд (абсолютная частота разряда), затем вычисляется относительная частота разряда:
p*j=nj/n (j=).
Статистический ряд строится в виде таблицы.
2.1.5. Построение статистических оценок функции распределения
Статистическая оценка функции распределения
Эмпирической (статистической) функцией распределения называют функцию 
(x), определяющую для каждого значения x относительную частоту события {X x}.
Из теоремы Бернулли следует, что при неограниченном увеличении n относительная частота события Х< х, т. е. (x) стремится по вероятности к F(x) этого события, так как 
.
Отсюда следует целесообразность использования эмпирической функции распределения выборки для приближенной оценки теоретической функции распределения случайной величины.
Реализация статистической функции распределения F*(x) рассчитывается по формуле:
F*(x) = 
,
где 
число значений вариационного ряда с учетом кратности, расположенных левее x, n – объем выборки.
Пример графика статистической функции распределения представлен на рис.1, из которого видно, что F*(x) представляет собой ступенчатую функцию.
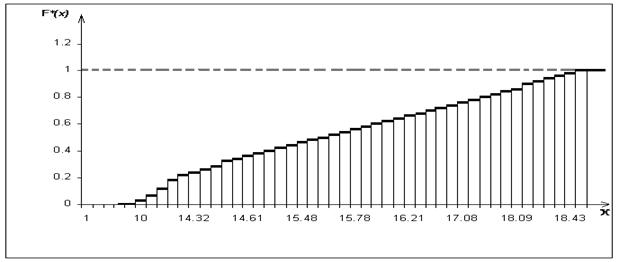
Рис.1. Статистическая функция распределения.
Кумулятивная ломаная
Кумулятивная ломаная является второй оценкой функции распределения.
При достаточно больших объемах выборки измерений (наблюдений) построение на основе всех вариационного ряда ступенчатой оценки F*(x) становится неудобным.
В этом случае для построения оценки функции распределения удобнее использовать данные статистического ряда, а именно:
F**(
) = 0
F**(
) = 
F**(
) = +
………………….
F**(
) = 
= 
,
где = 1.
Используя эти формулы, можно построить ломаную F**(x), проходящую через точки (
), j=
и принять ее в качестве второй оценки функции распределения, которая называется кумулятивной ломаной.
Пример расчетов приведен в табл.4.
Номер интервала | 1 | 2 | 3 | 4 | 5 | 6 |
Границы интервалов | [14,01; 14.74) | [14.74; 15.58) | [15.58; 16.32) | [16.32; 17.93) | [17.93;18.71) | [18.71; 19.55] |
Относительная частота интервалов | 0.18 | 0.16 | 0.16 | 0.16 | 0.16 | 0.16 |
F**(x) | 0.18 | 0.34 | 0.48 | 0.64 | 0.84 | 1 |
Таблица 4
График кумулятивной ломаной, построенной на основе данных табл.4, представлен на рис.2.
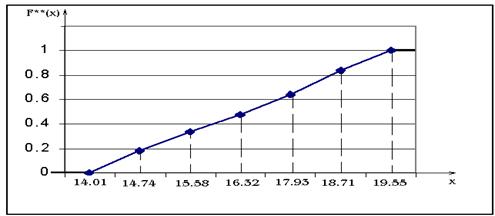
Рис.2. Кумулятивная ломаная
2.1.6. Построение статистических оценок плотности распределения
Статистическими оценками плотности распределения являются полигон частот и гистограмма.
Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат интервалы (разряды) статистического ряда длиною 
, а высота равна отношению 
(плотность относительной частоты). Площадь гистограммы относительных частот равна сумме всех относительных частот, т. е. единице.
Учитывая свойство плотности распределения можно записать:
P(xj-1 
X<xj )= f(
j)*lj , (j=
) , где lj – длина j-го интервала, f(j) – средняя на интервале плотность распределения f(x).
Заменяя P(xj X<xj+1 ) относительной частотой p*j статистического ряда, получим следующее выражение для приближенного значения f*j плотности распределения на интервале (разряде):
f*j= p*j/ lj , j= .
Таким образом, гистограмма относительных частот строится следующим образом: на оси Оx отложим границы разрядов и на них, как на основаниях, построим прямоугольники, имеющие площадь p*j и высоту равную f*j (см. рис.3.).
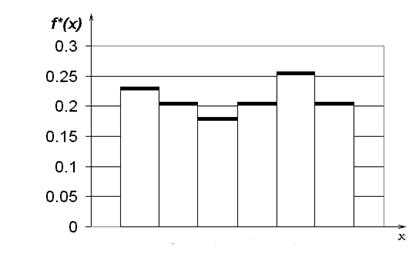
Рис.3. Оценка плотности распределения, построенная по относительным частотам
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат интервалы длиною 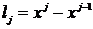, а высота равна отношению 
(см. рис.4.).
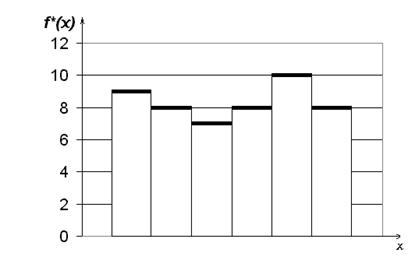
Рис.4. Оценка плотности распределения, построенная по частотам nj
Сглаженную гистограмму относительных частот в виде ломаной линии называют полигоном относительных частот, являющимся вторым способом оценки f(x). Она строится по точкам (
, 
) , j=
(см. рис. 5).
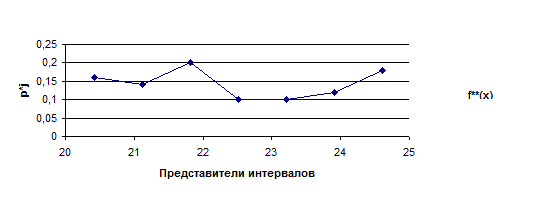
Рис.5. Полигон относительных частот
Полигон частот строим по точкам, координаты которых равны (, nj) , j= (см. рис.6).
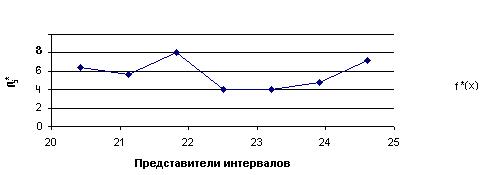
Рис.6. Полигон частот
2.2. Проверка статистических гипотез о законе распределения случайной величины по критериям согласия
2.2.1. Критерий согласия χ 2 Пирсона
Критерием согласия χ 2 Пирсона называют критерий проверки гипотезы о предполагаемой плотности распределения f(x).
Пусть имеется выборка измерений xn=(x1,…,xn) и требуется проверить гипотезу Но, состоящую в том, что непрерывная случайная величина Х имеет закон нормальный распределения (закон Гаусса). В данном случае в качестве гипотезы выступает параметрический закон распределения с плотностью распределения f(x/ ).
Гипотезу Но формируют в виде Х є f(x/ ), где – точечная оценка параметра (найденная по методу максимального правдоподобия).
Тогда алгоритм проверки состоит в следующем:
1. Формулируем гипотезу Но: случайная величина имеет закон распределения f0(x, 1,…, 
r) с r неизвестными параметрами 1,…, r.
2. По выборке измерений методом максимального правдоподобия находим точечные оценки неизвестных параметров 1,…, r. (например, необходимо найти точечные оценки двух параметров нормального закона m и σ2).
3. Разбиваем выборку на q интервалов, находим их границы хj ( j=) и частоты 
(используем данные статистического ряда).
4. Вычисляем вероятность попадания случайной величины в j-ый интервал по формуле:
, j=.
5. Вычисляется наблюдаемое значение критерия:
.
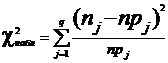6. Используя таблицу критических точек распределения χ2 , по заданному уровню значимости α и числу степеней свободы k=q-r-1, где q – число интервалов (разрядов), а r – число параметров предполагаемого закона, находят критическую точку χ2кр(α; k).
Если (
<χ2кр), гипотеза Н0 принимается;
Если ( 
χ2кр), гипотеза Н0 отклоняется.
Показано, что точность выводов повышается, если разряды выбирают с соблюдением условия: каждый разряд содержит не менее пяти реализаций хi.
2.2.2. Критерий согласия Колмогорова
Критерием согласия Колмогорова называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения F(x).
Критерий применяется для проверки гипотезы о непрерывной функции распределения случайной величины X.
Пусть заранее известно, что функция распределения исследуемой случайной величины X – непрерывная. Выдвинем гипотезу
,
то есть предположение, что функцией распределения случайной величины является выбранная нами из каких-то соображений непрерывная функция F(x).
Требуется принять или отклонить эту гипотезу по реализации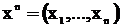 
случайной выборки 
независимых измерений X.
Для решения этой задачи введем статистику критерия проверки гипотезы 
в виде случайной величины:
,
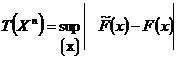где 
– статистическая функция распределения.
Реализация t статистики 
, соответствующая выборке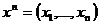 
, может быть найдена по формуле
, (2)
где 
– реализация статистической функции распределения .
Доказано, что ( если H – истинна)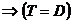 
.
Здесь D – случайная величина, распределенная по известному закону Колмогорова. Для этой величины, используя таблицы или формулы распределения Колмогорова, можно найти 
из условия:
,
где 
– вероятность практически невозможного события, и, следовательно, событие 
– практически невозможное.
Из предыдущих соотношений следует: [ если - истинна]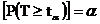 
, то есть: [если - истинна] 
[
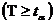- практически невозможно].
Теперь с точностью до принципа практической уверенности можно утверждать, что если гипотеза истинна, то реализации t статистики Т не могут превосходить границы . Далее по закону контрапозиции математической логики находим, что с той же точностью из неравенства 
следует ложность гипотезы . Итак, с точностью до принципа практической уверенности имеем:
( – истинна) 
;
( – ложна).
Из этих соотношений следует, что неравенство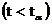
необходимо для принятия, а неравенство 
достаточно для отклонения гипотезы Н (с точностью до принципа практической уверенности).
Руководствуясь этими соображениями, принимают следующее правило решения поставленной задачи:
( – принять);
(3)
( – отклонить);
Правило (3) называют критерием согласия Колмогорова проверки гипотезы о непрерывной функции распределения случайной величины. Алгоритм его, очевидно, состоит в следующем:
1. Провести независимые n-кратные измерения случайной величины X с непрерывной функцией распределения и получить выборку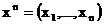 
.
2. Исключить из выборки грубые ошибки.
3. Построить реализацию статистической функции распределения.
4. Выдвинуть гипотезу F(x) о функции распределения случайной величины X.
5. Вычислить параметр t по формуле 2.
6. Задать вероятность практически невозможного события и из таблиц распределения Колмогорова найти параметр .
7. Принять или отклонить гипотезу .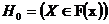
Доказано, что критерий состоятельный и в общем случае смещенный. Он более чувствителен к различию гипотез, поэтому при прочих равных условиях может применяться для меньших объемов выборки. Поскольку результат проверки критерия t зависит от наибольших различий и F(x), то нет необходимости построения и F(x) на всем диапазоне изменения x; достаточно ограничиться областью наибольших различий и F(x). Недостатком критерия является то, что точность его выводов нарушается, если в формировании гипотезы о F(x) используются характеристики эмпирических распределений, так как в этом случае статистика Т зависит от F(x). Известные неудобства доставляет также значительная трудоемкость построения статистики .
3. Требования к оформлению пояснительной записки к расчетно-графической работе
Расчетно-графическая работа оформляется на листах формата А4 и содержит следующие разделы:
1. Задание на расчетно-графическую работу
2. Исходные данные к расчетно-графической работе
3. Постановка задачи и математическое моделирование объектов задания расчетно-графической работы, описание методов исследования
4. Выполнение расчетно-графической работы
5. Выводы
6. Список литературы
7. Приложение.
Требования к набору текста: размер шрифта 14, шрифт Times New Roman, межстрочный интервал полуторный, выравнивание абзаца «По ширине», первая строка имеет отступ 1,5 см. Нумерация таблиц сквозная. Нумерация графиков сквозная. Графики имеют подрисуночную подпись. На все таблицы и графики должны быть ссылки в тексте. Примеры оформления таблиц и графиков приведены в разделе 4 данных методических указаний.
Все разделы расчетно-графической работы должны оформляться с использованием средств MS Windows (Word, Excel, Paint).
4. Пример выполнения расчетно-графической работы
4.1. Исходные данные к расчетно-графической работе
4.1.1. Получение выборки измерений
Проводится измерение времени, за которое выполняется дефрагментация жесткого диска. Всего проводится 50 измерений, представленных в табл.5. «Выборка измерений».
Выборка измерений
Таблица 5
№ измерения | Время дефрагментации, с | № измерения | Время дефрагментации, с |
1 | 281 | 26 | 305 |
2 | 325 | 27 | 297 |
3 | 272 | 28 | 304 |
4 | 308 | 29 | 260 |
5 | 293 | 30 | 275 |
6 | 310 | 31 | 309 |
7 | 281 | 32 | 287 |
8 | 279 | 33 | 294 |
9 | 331 | 34 | 282 |
10 | 263 | 35 | 278 |
11 | 291 | 36 | 326 |
12 | 329 | 37 | 321 |
13 | 295 | 38 | 298 |
14 | 263 | 39 | 306 |
15 | 326 | 40 | 283 |
16 | 286 | 41 | 313 |
17 | 307 | 42 | 296 |
18 | 292 | 43 | 314 |
19 | 270 | 44 | 290 |
20 | 281 | 45 | 311 |
21 | 320 | 46 | 291 |
22 | 305 | 47 | 300 |
23 | 315 | 48 | 280 |
24 | 294 | 49 | 295 |
25 | 315 | 50 | 283 |
Вариант 9
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
