МАГИЧЕСКИЕ КВАДРАТЫ И ИХ СОСТАВЛЕНИЕ

В MICROSOFT EXCEL

Математика. Исследование.

Автор: Мжельский Артём, 7А класс, МБОУ ШР« СОШ №1» , г. Шелехов, e-mail: *****@***ru

Руководители: , учитель математики, МБОУ ШР « СОШ №1», г. Шелехов, e-mail: *****@***ru

, учитель информатики, МБОУ ШР « СОШ №1», г. Шелехов, e-mail: *****@***ru

Web-адрес: http://*****/index. php/distantsionnoe-obrazovanie? id=84

Введение

Высшее назначение математики – находить порядок в хаосе,

который нас окружает.

Норберт Винер

Составление магических, или волшебных, квадратов — старинный и еще сейчас весьма распространенный вид математических развлечений. Задача состоит в отыскании такого расположения последовательных чисел (начиная с 1) по клеткам разграфленного квадрата, чтобы суммы чисел во всех строках, столбцах и по обеим диагоналям квадрата были одинаковы.

На факультативных занятиях в 5 классе мы изучали методы составления магических квадратов. Меня заинтересовала данная тема, и я решил побольше узнать об этих квадратах.

В сборниках нестандартных задач по математике часто встречаются задачи на составление магических квадратов. Кроме того, такие задания нередко включают в математические олимпиады, поэтому ребятам, увлекающимся математикой, полезно знать способы решения задач такого типа. Это определяет актуальность темы данного исследования.

Цель работы - изучить некоторые способы заполнения магических квадратов (Баше, Раус-Болла, сиамский (А. де ла Лубера), диагональный, двойной четности); составить их модели, используя MS Excel и проверить симметричность узоров магических линий.

Для достижения поставленной цели необходимо решить следующие задачи:

· ознакомиться с историей появления магических квадратов;

· выяснить виды магических квадратов;

· ознакомиться с различными методами заполнения магических квадратов;

· разработать в Microsoft Excel модели заполнения магических квадратов;

· рассмотреть симметричность узоров магических линий.

Объект исследования: магический квадрат и методы его заполнения.

Предмет исследования: возможность заполнения магических квадратов с использованием Microsoft Excel.

При работе применялись следующие методы:

· поисковый метод с использованием научной и учебной литературы, а также поиск необходимой информации в сети Интернет;

· практический метод составления магических квадратов на основе полученных знаний; разработка в программе Microsoft Excel моделей заполнения магических квадратов;

· исследовательский метод при рассмотрении симметричности узоров магических линий;

· анализ полученных в ходе исследования закономерностей.

История появления магических квадратов

Говорить люди умели раньше, чем научились фиксировать сказанное. И простейшие вычисления с использованием условных единиц в виде пальцев, палочек, камешков, узелков появились еще до того, как люди смогли записать это. Но доказательно судить о том, что и когда научился делать человек в своем развитии, мы можем только на основе дошедших до нас вещественным и письменных источников.

Точно можно утверждать, что история магических квадратов начинается в древнем Китае. В ранних литературных сочинениях, написанных там еще до нашей эры, появляются упоминания о некой схеме «ло-шу», которую «мудрые берут за образец». Изображение магического квадрата в виде связанных кружков встречайся в более позднем трактате мыслителя Чжу Си. Вот как эффектно он выгля­дел там:

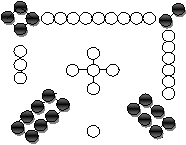Черные кружки - это четные (женственные) числа, белые - не­четные (мужественные) числа.

Существует несколько легенд о происхождении этого пер­вою магического квадрата, часто называемого «ло-шу». Скорее всего, это просто выдумки, потому что известно несколько абсо­лютно разных толкований, которые даются со ссылками на различные древние книги, но противоречат друг другу. Пальма первенства в этом открытие у Китая.

Так выглядит этот квадрат в обычной числовой форме. В дальнейшем, занимаясь магическими квадратами, китайские математики рассматривали квадраты не только третьего, но и более высоких порядков, придумали правила для их построения.

В древнеиндийских надписях и трактатах встречаются изо­бражения магических квадратов четвертого порядка.

Второй из этих квадратов сохраняет свойство быть магическим и после того, как его строки или столбцы циклически перемещаются, соответственно сверху вниз или слева направо. Иначе говоря, если сделать плоский непрерывный ковер с узором из таких квадратов, то, вырезав любую его часть из 4 строк и 4 столбцов, получаем снова ма­гический квадрат.

Из Индии сведения о магических квадратах перешли к арабам. Арабы были знакомы с квадратом третьего порядка в VIII веке, а в XII веке его описал в своих сочинениях Ибн Эзра, испанский еврей, принявший мусульманство. Мусульмане очень благоговейно относились к квадратам пятого порядка с цифрой 1 в середине, считая это изображение символов единства Аллаха. В Европе о магических квадратах узнали благодаря византийскому писателю Э. Мосхопулосу, жившему в Константинополе в начале XV века.

Редкостью является использование магического квадрата в изобразительном искусстве, а не в литературном или научном произведении. Впервые это сделал немецкий художник Альбрехт Дюрер (), выпустивший в 1514 году гравюру «Мелан­холия», на которой в правом верхнем углу есть изображение магического квадрата четвертого порядка. Причем два числа в середине нижней строки указывают на год создания гравюры - 1514. Этот факт говорит об умении в то время составлять магиче­ские квадраты с определенным заданным расположением некото­рых чисел. Говорят, что гравюра А. Дюрера послужила толчком для знаменитых пророчеств его современника Мишеля Ностра­дамуса ().

Известный немецкий гуманист () построил магические квадраты порядков 3, 4, 5, 6, 7, 8, 9 — он связал их с семью астрологическими «планетами» — Са­турном, Юпитером, Марсом, Солнцем, Венерой, Меркурием, и Луной. Слово планеты взято в кавычки потому, что Луна и Солн­це, как известно, проходят по другим категориям небесных тел. В Западной Европе в средние века магические квадраты были дос­тоянием представителей алхимии и астрологии. Серебряные пла­стинки с выгравированными магическими квадратами носили как амулеты, предохраняющие от чумы и других бед и поветрий. От суеверных представлений древних китайцев, индусов, европей­ских алхимиков и астрологов эти числовые квадраты и получили свое необычное для математики название - «магические» квадраты. Иногда по отношению к ним употребляется слово «волшебные», но значительно реже, чем «магические».

В наш просвещенный век снова в почете астрологи, колдуны и магистры магии. Один из современных колдунов, Магистр Белой магии Юрий Лонго предлагал через газету «Комсомольская правда» бесплатно выслать Магический Квадрат, который помо­жет избавиться от финансовых трудностей, невезения, проблем в любви. Очень много мистических словоизлияний, посвященных магическим квадратам и магическим свойствам чисел, можно найти в Интернете.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8