Составление магических квадратов было делом не только астрологов или бездельников, ищущих забавы. Теорию их раз­рабатывали многие выдающиеся математики. В 1654 году французский ученый Блез Паскаль написал трактат, полностью посвященный магическим квадратам. В дальнейшем к теории магических квадратов обращались многие выдающиеся мате­матики. Она находит применение в ряде важных математических вопросов. Выводы теории магических квадратов используются в одном из методов решения систем уравнений со многими неиз­вестными и даже в современной квантовой механике. В теории квантования моментов количества движения, используется так называемая таблица Редже, которая представляет собой магический квадрат 3x3, составленный из произвольных чисел.

А любителям математики составление квадратов служило хорошей гимнастикой ума и одно время столь же процветало, как увлечение кроссвордами в наши дни. Особо усердным хватало терпения, чтобы составить, например, квадрат 43-го порядка с числами от 1 до 1849. Один только факт: в 1838 году, когда о магических квадратах было известно намного меньше, чем теперь, во Франции был напечатан трактат на эту тему, состоящий из трех объёмных томов. Однако полного описания всех возможных магических квадратов не получено и до сегодняшнего дня.

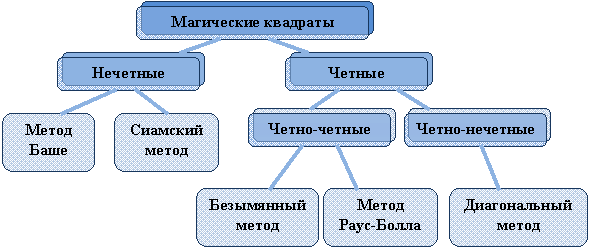Рассмотрев некоторые методы, мы классифицировали магические квадраты по категориям:

Методы составления магических квадратов

Общий метод построения квадратов неизвестен, хотя широко применяются различные частные алгоритмы. Некоторые из них рассмотрим ниже.

Метод Баше

Самый простой прием составления магических квадратов нечетного порядка, то есть квадратов из любого нечетного числа клеток: 3x3, 5х5, 7х7 и т. п., придумал в XVII веке французский математик Клод Гаспар Баше.

Итак, приступим к состав­лению 9-клеточного магического квадрата по способу Баше.

1.Квадрат дополняется вспомогательными клетками с четы­рех сторон «лесенкой» или «террасами» как показано на рисунке.

2. Последовательные числа от 1 до n выписываются ряд за рядом в направлении, параллельном одной из диагоналей квадрата.

3.Числа, оказавшиеся за рамками квадрата, нужно ввести внутрь. Для этого «террасы» мысленно вдвигаем в квадрат так, чтобы они примкнули к противолежащим сторонам квадрата.

Вот какой квадрат 3-го порядка полу­чается в итоге.

Способ Баше очень прост, на практике его можно применять для построения нечетных квадратов сколь угодно высокого по­рядка, но он дает только один из множества возможных вариантов.

Применим метод Баше к составлению квадрата из 5х5 клеток. Начинаем с расположения:

Остается только числа, оказавшиеся за рамками ква­драта, ввести внутрь его. Для этого нужно фигуры, образо­ванные числами, стоящими вне квадрата («террасы»), мысленно вдвинуть в квадрат так, чтобы эти фигуры при­мкнули к противолежа­щим сторонам квадрата. По­лучится магический 25-клеточный квадрат.

Сиамский метод (А. де ла Лубера)

Магические квадраты нечетного порядка также можно построить с помощью метода французского геометра XVII в. А. де ла Лубера (сиамский метод). Рассмотрим этот метод на примере квадрата 5-го порядка.

1.  Число 1 помещается в центральную клетку верхней строки. Все натуральные числа располагаются в естественном порядке циклически снизу вверх в клетках диагоналей справа налево. Дойдя до верхнего края квадрата, продолжаем заполнять диагональ, начинающуюся от нижней клетки следующего столбца (по ломаной диагонали).

2.  Дойдя до правого края квадрата, продолжаем заполнять диагональ, идущую от левой клетки строкой выше.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8