2 | |||||
1 | |||||
4 | 4 | ||||
3 | |||||
2 |
3. Дойдя до заполненной клетки или угла, траектория спускается на одну клетку вниз, после чего процесс заполнения продолжается.
2 | |||||
1 | |||||
5 | |||||
4 | 6 | 4 | |||
3 | |||||
2 |
Получится магический квадрат 5 порядка.
18 | 25 | 2 | 9 | ||
17 | 24 | 1 | 8 | 15 | 17 |
23 | 5 | 7 | 14 | 16 | 23 |
4 | 6 | 13 | 20 | 22 | 4 |
10 | 12 | 19 | 21 | 3 | 10 |
11 | 18 | 25 | 2 | 9 |
Магические квадраты порядка двойной чётности
Для составления магических квадратов с четным числом клеток еще не найдено общего и удобного правила. Сравнительно простой прием существует для таких четных квадратов, число клеток которых делится без остатка на 16; число клеток в стороне этих квадратов кратно 4, то есть сторона их состоит из 4, из 8, из 12 и т. д. клеток.
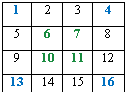
1. Выпишите все числа от 1 до n2 по порядку в строках квадрата.
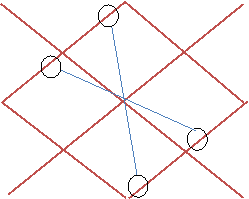
2. Числа, стоящие в диагональных клетках, поменяйте местами с числами симметрично стоящими к ним относительно центра квадрата.
|
|
Эти правила применимы для построения магического квадрата любой двойной четности. Только обмену подлежат числа, стоящие на диагоналях, каждого из квадратов 4x4, составляющих большой квадрат. Но центром симметрии по-прежнему является центр большого квадрата.
|
|
Метод Раус-Болла
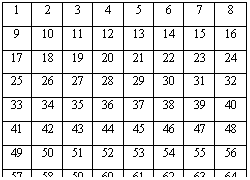
Метод Раус-Болла начинается с того, что квадрат заполняется слева направо и сверху вниз числами от 1 до n2 в их естественном порядке. Затем выполняются перестановки чисел в некоторых клетках, после чего квадрат становится магическим. Сначала рассмотрим случай, когда после деления квадрата на четыре равные части, каждая из них становится квадратом четного порядка. Для примера возьмем квадрат 8-го порядка.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 |