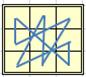
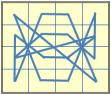
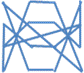
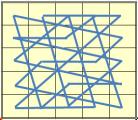
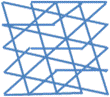
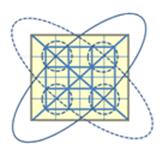
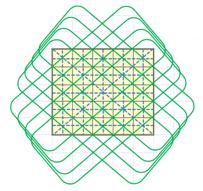
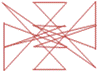
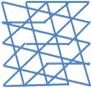
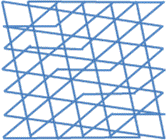
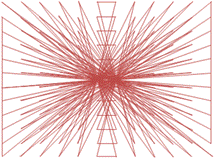
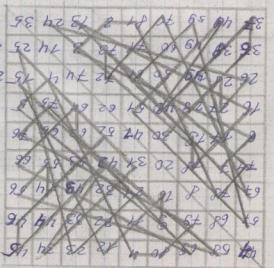
Вот примеры подобных орнаментов из магических линий. Для придания узору завершенности, соединим в конце последнее число с первым.

Интересный узор можно получить, если соединять линиями (не обязательно прямыми) все группы чисел, образующих при сложении магическую сумму.

Рассмотрев магические квадраты, составленные методом Баше, можно увидеть общие черты в узорах маги­ческих линий в квадратах разного порядка. Сравним характер линий квадратов, заполненных методами Баше и Раус-Болла.

Исследуя узоры магических линий некоторых способов заполнения квадратов, мы увидели, что получившиеся рисунки линий магических квадратов симметричны относительно центра (кроме диагонального метода). Если разделить квадрат на две равные части и в каждой части последовательно соединить числа, то полученные узоры тоже симметричны относительно центра квадрата.

Использование Microsoft Excel в построении магических квадратов

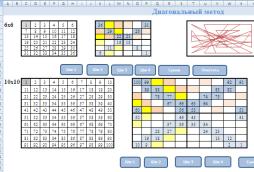
Так как для составления магических квадратов необходимо всегда проверять контрольные суммы по строкам, столбцам и диагоналям, мы пришли к выводу, что этот процесс лучше автоматизировать. Для автоматизации мы выбрали программу MS Excel.

Используя функции ЕСЛИ и СУММ, мы разработали модели[2] заполнения магических квадратов 3, 5, 7, 9 и 11 порядка по методу Баше и сиамскому методу; 4, 8, 12 порядка по безымянному методу и методу Раус-Болла; 6, 10 и 14 порядка по диагональному методу.

Рассмотрим модели 5 и 7 порядков по методу Баше.

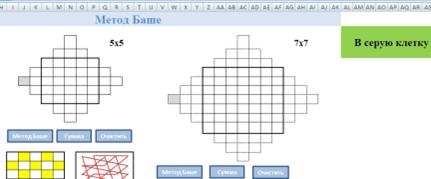
Для заполнения последовательных чисел от 1, необходимо в серую клетку напечатать цифру 1. После этого автоматически заполняются все последующие клетки по параллельным диагоналям.

Элементы по диагонали каждый раз увеличиваются на единицу от предыдущего элемента, стоящего в этой диагонали. С учетом этого, достаточно вручную ввести только первый элемент, а все остальные рассчитать по формулам.

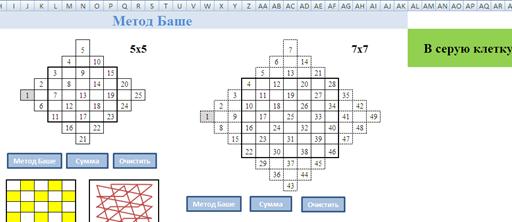
Для автоматического заполнения магического квадрата мы использовали кнопку Метод Баше, к которой назначили макрос[3] заполнения квадрата.

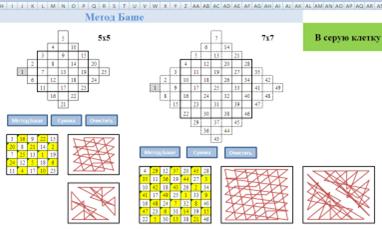
При нажатии на кнопку Сумма автоматически подсчитываются контрольные суммы по строкам, столбцам и диагоналям.

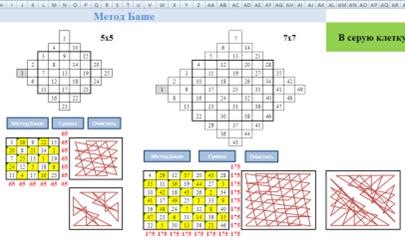
Для удобства повторного заполнения магического квадрата применили кнопку Очистить, которая очищает магический квадрат и ячейки с контрольными суммами.

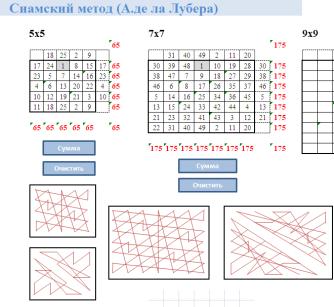
Рассмотрим модели 5 и 7 порядков по сиамскому методу (А. де ла Лубера).

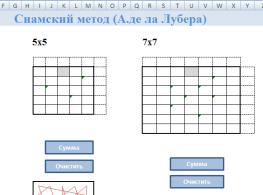
Для заполнения последовательных чисел от 1, необходимо в серую клетку напечатать цифру 1. После этого автоматически заполняются все последующие клетки по диагоналям.

При нажатии на кнопку Сумма автоматически подсчитываются контрольные суммы по строкам, столбцам и диагоналям.

Рассмотрим модели 8 и 12 порядков по безымянному методу (порядка двойной четности).

Для заполнения последовательных чисел от 1, необходимо в серую клетку напечатать цифру 1. После этого автоматически заполняются все последующие клетки по параллельным диагоналям.

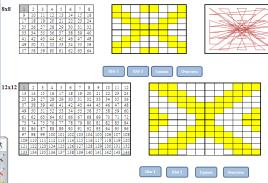
Для автоматического заполнения магического квадрата мы использовали кнопки Шаг 1 и Шаг 2, к которым назначили макрос[4] заполнения квадрата. При нажатии на эти кнопки соответственно заполняются неизменяющиеся клетки, а потом клетки, в которых значения заменяются на симметричные относительно центра.

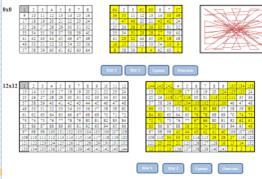
При нажатии на кнопку Сумма автоматически подсчитываются контрольные суммы по строкам, столбцам и диагоналям.

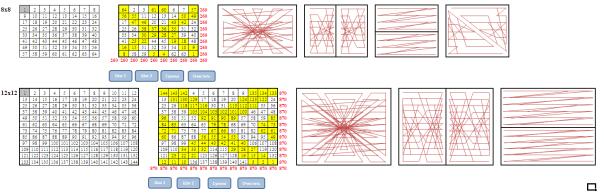
Рассмотрим модели 8 и 12 порядков по методу Раус-Болла.

Для заполнения последовательных чисел от 1, необходимо в серую клетку напечатать цифру 1. После этого автоматически заполняются все последующие клетки по параллельным диагоналям.

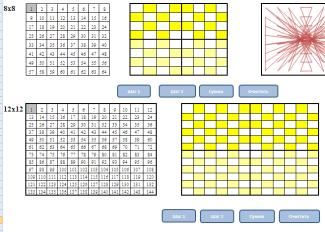
Для автоматического заполнения магического квадрата мы использовали кнопки Шаг 1 и Шаг 2, которые соответственно заполняют 1 и 4 квадраты; 2 и 3 квадраты.

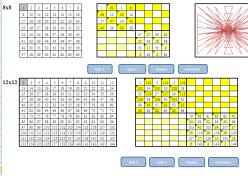
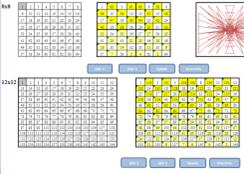
При нажатии на кнопку Сумма автоматически подсчитываются контрольные суммы по строкам, столбцам и диагоналям.

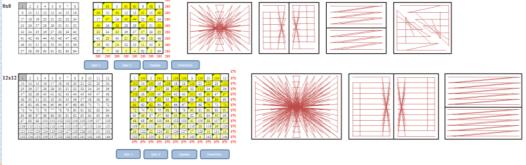
Рассмотрим модели 6 и 10 порядков по диагональному методу.

Для автоматического заполнения магического квадрата мы использовали кнопки Шаг 1, Шаг 2, Шаг 3 и Шаг 4.

При нажатии на кнопку Сумма автоматически подсчитываются контрольные суммы по строкам, столбцам и диагоналям.

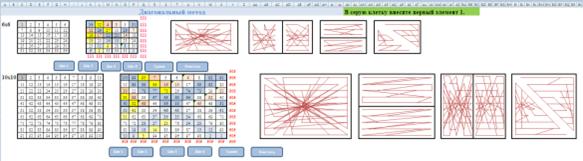
Для каждого магического квадрата мы получили узор магических линий.

В ходе экспериментальной части, мы пришли к выводу, что процесс заполнения квадратов нечетного порядка по методу Баше можно автоматизировать. Достаточно указать первый элемент и нажать на необходимые кнопки. А у магических квадратов порядка двойной чётности можно только автоматизировать один из вариантов заполнения и расчёт контрольных сумм. Так как по безымянному методу, начиная с 8 порядка возможны несколько вариантов заполнения магических квадратов.

Выводы

1.  Универсального способа заполнения магических квадратов нет.

2.  Способ заполнения магического квадрата, зависит от его порядка.

3.  Известные методы для заполнения нечетных квадратов можно автоматизировать. Для этого идеально подходит программа MS Excel.

4.  Узоры магических линий квадратов имеют общие черты и симметричны относительно центра квадрата (кроме диагонального).

5.  При делении квадрата на две равные части получаются узоры линий симметричны относительно центра квадрата (кроме диагонального).

Перспектива

В будущем планируется изучить другие методы составления магических квадратов и применить для их заполнения MS Excel. Проверить симметричность узоров магических линий квадратов, заполненных различными методами.

Список литературы

1.  Магия чисел и фигур. Занимательные материалы по математике/ авт.-сост. .- М.: Глобус, 2007.

2.  Перельман задачи и опыты. – Д.: ВАП, 1994.

3.  , . За страницами учебника математики. – Москва. Просвещение. 1989г.

4.  Энциклопедия Кругосвет (http://www. *****/enc/nauka_i_tehnika/matematika/MAGICHESKI_KVADRAT. html? page=0,0)

5.  Словари и энциклопедии на Академик http://dic. *****/dic. nsf/enc_colier/

Приложение

Метод Баше

Магический квадрат 15 порядка

Сиамский метод

Магический квадрат 11 порядка

Безымянный метод

Магический квадрат 4 порядка

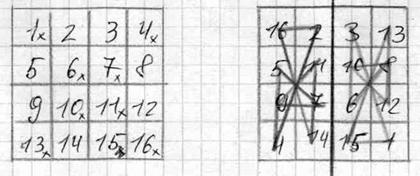
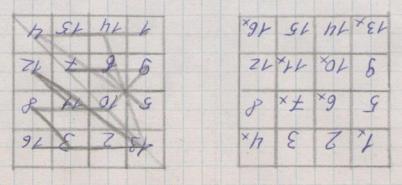
Магический квадрат 8 порядка

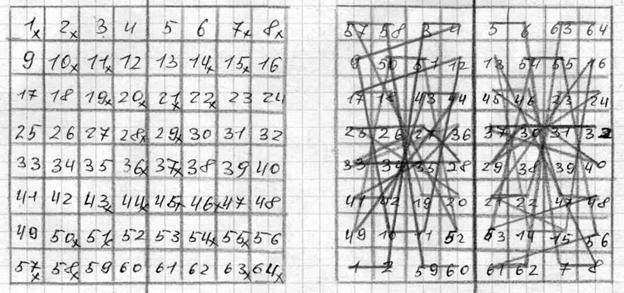
Магический квадрат 8 порядка

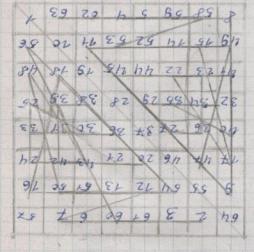
Магический квадрат 12 порядка

Магический квадрат 16 порядка

Магический квадрат 20 порядка

Метод Раус-Болла

Магический квадрат 8 порядка

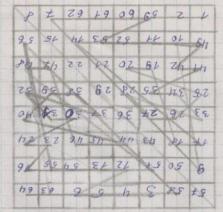
Магический квадрат 12 порядка

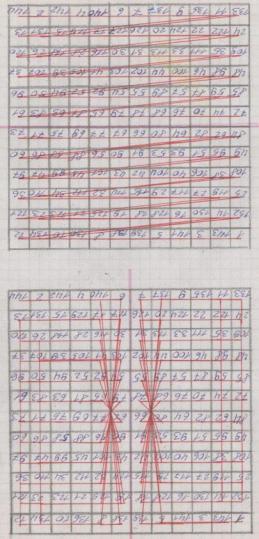
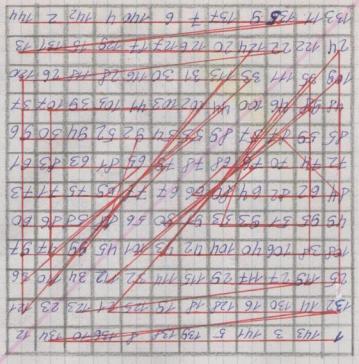
Магический квадрат 14 порядка

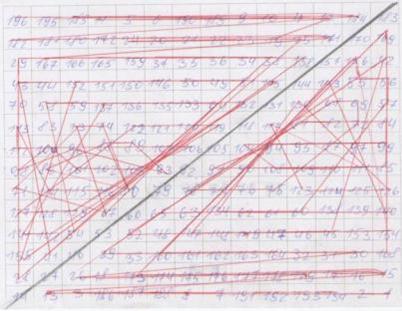
Диагональный метод

Магический квадрат 6 порядка

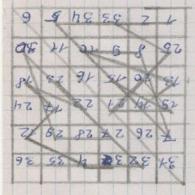
[1] Ломаной называется диагональ, которая, дойдя до края квадрата, продолжается параллельно первому отрезку от противоположного края, такую диагональ образуют заштрихованные клетки.

[2] Модель (от лат. modulus – «аналог, образец») – это упрощенное представление реального объекта.

[3] Макрос - последовательность нескольких команд, объединенных для выполнения определенной задачи. Макросы служат для ускорения выполнения действий, повторяющихся много раз.

[4] Макрос - последовательность нескольких команд, объединенных для выполнения определенной задачи. Макросы служат для ускорения выполнения действий, повторяющихся много раз.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8