Газовый смазочный слой в зазоре произвольной формы

УДК 514.86

Д. А. ПЕТРОВ

(», Санкт-Петербург)

ГАЗОВЫЙ СМАЗОЧНЫЙ СЛОЙ В ЗАЗОРЕ ПРОИЗВОЛЬНОЙ ФОРМЫ

Предложена форма записи уравнения Рейнольдса, описывающего установившееся течение в тонком зазоре в произвольной системе координат (при произвольной форме зазора) с учётом сжимаемости среды. Этот результат помогает в получении готового для постановки практических задач уравнения Рейнольдса в координатах.

Введение

Задачи расчёта подшипников газодинамического типа с зазорами разнообразной формы до сих пор остаются весьма актуальными. По-сути, они сводятся к изучению газового смазочного слоя в тонком зазоре произвольной формы. Решением таких задач занимается гидродинамическая теория смазки. Этот раздел механики жидкости и газа начал развиваться в конце XIX века вслед за потребностями техники. Начало теоретическому исследованию течений в тонких зазорах положили работы профессора Технологического института Н. П. Петрова и британского учёного Осборна Рейнольдса, уточнённые и доведённые до возможности практического применения А. Зоммерфельдом, А. Мичелем, и (их работы размещены в сборнике [2]). В этих классических работах, однако, рассматривалась лишь задача о непрофилированном радиальном подшипнике скольжения с жидкой смазкой. Дальнейшие исследования позволили распространить результаты созданной Рейнольдсом теории на газодинамические подшипники. Были даже предприняты успешные попытки (например, Пэном в статье [3]) получения общего вида уравнения Рейнольдса для смазочного слоя без привязки к конкретной системе координат. Предлагаемый доклад посвящён анализу используемых при выводе уравнения Рейнольдса предположений и получению не зависимой от избранной системы координат формы этого уравнения, пригодной (с минимальными усилиями) к использованию в практических задачах.

Исследование газового слоя в тонких зазорах

Результаты классической теории

Основоположником гидродинамической теории смазки обычно считают профессора Н. П. Петрова. В работе «Трение в машинах» [2] он дал, по-видимому, первую формулу момента сопротивления вращению цилиндрического вала в коаксиальной с ним неподвижной цилиндрической обойме. Формула была получена в процессе математического описания задачи, рассмотренной ранее Максом Маргулисом. не использовал в своих рассуждениях существовавшие уже уравнения, описывающие течение вязкой среды. Хотя, например, уравнение движения было впервые записано для жидкости французом Навье в 1822 году, а уравнение неразрывности для несжимаемой среды было получено Эйлером ещё в 1755 году.

Но настоящим основателем гидродинамической теории смазки стал Осборн Рейнольдс, опубликовавший в 1886 году работу «Гидродинамическая теория смазки и её применение к опытам Тоуэра» [2]. Рейнольдс не только ввёл сам термин «гидродинамическая теория смазки», не только указал на ламинарный характер течения в тонком зазоре, но сделал довольно успешную попытку математизации описания такого течения, получив основное уравнение, определяющее давление газа в потоке и ныне носящее его имя. Ламинарность течения Рейнольдс показал, сравнив величину зазора с отношением где: – вязкость газа, считаемая Рейнольдсом постоянной; – его плотность; – скорость потока в зазоре. Фактически он использовал критерий, который позднее получил обозначение [1] . Далее, полагая силы инерции и веса (массовые силы) несравненно меньшими, чем силы вязкости, Рейнольдс учёл практическую несжимаемость смазочного масла, задачу для течения которого он рассматривал. Основное уравнение Рейнольдс выписывает в виде [2]

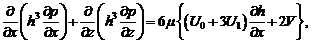(1)

где: – функция, определяющая величину зазора в данной точке; – давление среды в зазоре; и – скорости движения поверхностей, ограничивающих зазор. В этом уравнении в правую часть Рейнольдсом добавлен не следующий из вывода член В дальнейшем он используется для учёта движений одной из стенок зазора, меняющих значение функции Как видим, уравнение выписано в декартовых координатах. Однако в своей работе Рейнольдс использует его и для описания смазки цилиндрического подшипника. Предложенная Осборном Рейнольдсом гидродинамическая теория обрела законченный и готовый к практическому применению вид в работах А. Зоммерфельда, А. Мичеля, и [2]. Все указанные авторы исследовали только случай цилиндрического подшипника скольжения без профилирования поверхностей шипа и обоймы.

Анализ предположений и получение общего вида уравнения Рейнольдса

Рассмотрим подробнее процедуру вывода уравнения Рейнольдса. Обычно её начинают с уравнений Навье–Стокса. Уравнение Навье–Стокса, как известно, выражает закон сохранения импульса в вязкой сжимаемой среде, подверженной воздействию внешних массовых сил. Для упрощения его подвергают процедуре обезразмеривания с выделением безразмерных параметров, носящих название чисел Струхала, Фруда, Эйлера и Рейнольдса. Соотношения между этими параметрами определяются из предположений о характере течения среды. В случае с течением в тонких зазорах подробный анализ значения делаемых допущений о самой среде и характере её течения можно найти в монографии [1]. Здесь ограничимся перечислением наиболее существенных для получения интересующего нас приближения допущений: течение установившееся, медленное (ползучее), среда невесомая, термодинамически совершенная, температура постоянна во всей области течения. В этих предположениях система уравнений Навье–Стокса упрощается до

(2)

где: – оператор Гамильтона; – оператор Лапласа; вектор – скорость газа. Система замыкается уравнением состояния совершенного газа 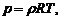где: – индивидуальная газовая постоянная; – абсолютная температура. В сделанных предположениях данное уравнение эквивалентно условию пропорциональности давления плотности. Запись системы уравнений (2) в векторном виде показывает, что пока ни одно из введённых допущений не ограничивает нас в выборе системы координат. Ограничения начинают появляться на следующем этапе упрощения, когда необходимо учесть малость зазора, то есть малость отношения где: – характерная величина зазора; – характерный линейный размер вдоль течения.

На этом этапе уравнения можно записать в ортогональной криволинейной системе координат 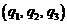, выбираемой так, чтобы координата отсчитывалась по нормали к зазору, а – в направлении движения перемещаемой стенки зазора. Условия, накладываемые на выбор координат, их порядка, направлены именно на облегчение учёта малости зазора. Использование описанных координат преобразует уравнения движения из системы (2) к форме

(3)

где: – коэффициенты Ламе; – компоненты вектора скорости . Это уравнение легко разрешается относительно скорости, если только одна из стенок зазора вместе с прилегающим к ней слоем газа имеет скорость в направлении , а остальные компоненты скорости газа на стенке равны нулю. Выражения, получаемые интегрированием уравнений (3), будут такими:

(4)

где: – нормированная на величину зазора координата. Средние по зазору скорости определяются выражениями

(5)

Переходя теперь к первому уравнению системы (2), записываем его в координатах и интегрируем по зазору, получая

(6)

Подстановка в это уравнение ранее полученных средних скоростей даст уравнение Рейнольдса. Но для более удобной записи его необходимо ещё раз привести к безразмерному виду, выделяя параметр

(7)

где: – характерная скорость; – характерное давление. Этот параметр называют числом сжимаемости или числом Гаррисона. В результате, уравнение запишется в виде

(8)

Это и есть уравнение Рейнольдса для произвольной формы зазора. Из него подстановкой конкретных коэффициентов Ламе легко получить уравнение для любой фигурирующей в задаче формы зазора газодинамической опоры. Например, при использовании сферической системы координат получается уравнение для зазора сферической формы

(9)

а при использовании цилиндрических координат – сразу два важных случая. Это уравнение для цилиндрического (радиального) подшипника

(10)

и уравнение для плоского упорного подшипника

(11)

Сравнение с результатами Пэна

При подготовке данного доклада к публикации автор ознакомился со статьёй Пэна [3], в которой при помощи тензорного исчисления также был получен обобщенный вид уравнения Рейнольдса, не зависящий от координат. Следует отметить, что Пэн в качестве исходной системы берёт упрощённые в соответствии с предположениями смазочного слоя уравнения движения вместе с нестационарным (полным) уравнением неразрывности. Он постулирует, что напряжения вязкого сдвига обычно превосходят массовые силы инерции. Это требование эквивалентно ползучести течения, а также, по-видимому, невесомости среды. В общем, отличие заключается только в отказе от рассмотрения лишь установившегося течения. Пэн также рассматривает более общий вид метрического тензора, что позволяет применять его результат и в неортогональных координатах. Наконец, он рассматривает подвижность обеих стенок зазора, хотя это и представляется излишним в виду возможности привязки координат к одной из подвижных стенок и использования принципа относительности движения.

Общность использованных Пэном предположений такова, что на практике в подавляющем большинстве случаев не используется, достаточно представленного в настоящей статье результата.

Заключение

В докладе представлен вывод уравнения Рейнольдса для установившегося течения в газовом смазочном слое в зазоре произвольной формы. Уравнение Рейнольдса занимает ключевое место в проблемах расчёта газодинамических подшипников, а представленный результат позволяет легко получить важные частные случаи для решения часто встречающихся задач.

ЛИТЕРАТУРА

1.  Дроздович, В. Н. Газодинамические подшипники. - Л.: Машиностроение, 19с.

2.  Лейбензон, Л. С. Гидродинамическая теория смазки // под ред. Л. С. Лейбензона. - М., Л.: Гостехиздат, 19 с.

3.  Пэн, Сферические подшипники скольжения с газовой смазкой // Техническая механика, № 2. - М.: Мир, 1963. - С. 219 – 230.

Работа выполнена самостоятельно.