Министерство образования Российской Федерации
Южно-Уральский государственный университет
Филиал в г. Златоусте
Кафедра технической механики
531(07)
К142
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Часть 5
ДИНАМИКА СИСТЕМЫ ТОЧЕК
Учебное пособие для самостоятельного изучения студентами
Челябинск
Издательство ЮУрГУ
2002
УДК 531(075)
Казанцева механика: В 6 частях. Часть 5. Динамика системы точек: Учебное пособие для самостоятельного изучения студентами. — Челябинск: Изд-во ЮУрГУ, 2002. — 68 с.
Учебное пособие предназачено для самостоятельного изучения разделов теоретической механики «Введение в динамику системы», «Основные теоремы динамики системы точек». Пособие состоит из теоретической и практической частей. В разделе «Ответы и решения» даны примеры решения задач и анализ типичных ошибок, допускаемых студентами при их решении.
Пособие предназначено для студентов всех технических специальностей.
Ил. 93, список лит. — 4 назв.
Одобрено учебно-методической комиссией филиала ЮУрГУ в г. Златоусте.
Рецензенты: ,
© Издательство ЮУрГУ, 2002.
ВВЕДЕНИЕ
Программированное обучение базируется на достижениях кибернетики как науки об общих закономерностях процессов передачи информации и управления ею.
Программированное обучение представляет собой совокупность методов и средств оптимизации массового обучения на основе последовательного осуществления принципа программированного управления. Главная задача высшей школы — повышения качества обучения, поэтому кафедра технической механики ЗФ ЮУРГУ рассматривает программированное обучение, прежде всего как систему управляемой самостоятельной работы студентов.
Основные требования к такой системе
1. Увеличение числа часов на самостоятельную работу студентов во время, регламентированное расписанием.
2. Обеспечение всех студентов учебниками и учебно-методическими пособиями.
3. Самостоятельная работа в аудитории должна проходить под контролем преподавателя.
4. Самостоятельная работа как аудиторная, так и домашняя должна сопровождаться самоконтролем студентов в процессе обучения и достаточно частым и эффективным контролем преподавателя по отдельным этапам изучаемого курса.
5. Должна быть представлена возможность изучения курса в темпе, определяемом индивидуальными способностями каждого студента.
6. Система должна обеспечить логическую связь между всеми формами учебного процесса: лекции, практические занятия, самостоятельная работа дома и в аудитории.
Раздел 1. ВВЕДЕНИЕ В ДИНАМИКУ СИСТЕМЫ
Раздел состоит из двух тем.
После его изучения студент должен
знать: а) определения механической системы и классификацию сил, действующих на систему; б) понятие центра масс системы; в) понятие моментов инерции и радиуса инерции; г) формулировку теоремы о моментах инерции относительно параллельных осей; е) формулы для вычисления моментов инерции однородных тел; ж) формулы для вычисления осевых полярных, центробежных моментов инерции тела; з) формулы для вычисления моментов инерции тела относительно различных осей;
уметь: а) практически вычислять моменты инерции однородных тел правильной формы; б) практически применять теорему о моментах инерции относительно параллельных осей; в) вычислять моменты инерции тела относительно точки, оси; г) определять практически положение центра масс системы.
Тема 1. ПОНЯТИЕ МЕХАНИЧЕСКОЙ СИСТЕМЫ
Механической системой или системой материальных точек называется совокупность точек, связанных между собой так, что движение каждой точки системы зависит от движения остальных точек системы.
Примером механической системы является всякое абсолютно твердое тело или же совокупность тел, связанных между собой.
Выбор механической системы зависит от нас, так как, изучая движение какого-либо механизма, можно в зависимости от характера поставленной задачи принять за механическую систему как весь механизм в целом, так и любое его звено.
В динамике различают изменяемые и неизменяемые системы точек.
Система называется неизменяемой, если точки ее не перемещаются относительно друг друга, изменяемой, если точки системы перемещаются относительно друг друга.
Всякое абсолютно твердое тело можно рассматривать как неизменяемую систему. Примером изменяемой системы являются деформируемое (не абсолютно твердое) тело.
Классификация сил, действующих на систему.
В динамике принято делить все силы, действующие на систему точек, на два вида: внутренние и внешние.
Внутренними ![]() называются силы, с которыми точки или тела, составляющие систему, действуют друг на друга.
называются силы, с которыми точки или тела, составляющие систему, действуют друг на друга.
Внешними ![]() называются силы, с которыми действуют на систему точки или тела, не входящие в состав самой системы.
называются силы, с которыми действуют на систему точки или тела, не входящие в состав самой системы.
Если деление сил на активные и реакции связи зависит от физической природы сил, то деление их на внешние и внутренние зависит от нашего выбора. Одна и та же сила может быть внешней по отношению к одной системе точки внутренней по отношению к другой. Таким образом, деление сил на внешние и внутренние является условным и зависит от того, что включим в состав системы.
Пример. Если рассмотреть движение всей солнечной системы в целом, то сила притяжения Земли к Солнцу будет внутренней. Если же рассмотреть Землю как систему точек, то эта сила станет внешней.
Свойства внутренних сил системы
1. Геометрическая сумма всех внутренних сил системы равна нулю, то есть

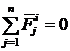 .
.
Действительно, на основании третьего закона динамики силы, с которыми действуют друг на друга точки системы, равны по величине и противоположны по направлению (рис.1).
![]()
![]()
![]()
![]()
Складывая такие силы, получаем: 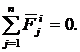
2. Геометрическая сумма моментов всех внутренних сил относительно любого центра О равна нулю, т. е. 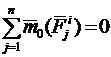 (рис. 2). Для любой пары точек системы
(рис. 2). Для любой пары точек системы 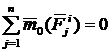 , так как
, так как
![]() ,
,
потому что ![]()
![]() и
и ![]() — коллинеарны.
— коллинеарны.
 Полученные выводы упрощают исследования вопросов, относящихся к системе точек, так как они позволяют в некоторых случаях не принимать в расчет внутренние силы системы.
Полученные выводы упрощают исследования вопросов, относящихся к системе точек, так как они позволяют в некоторых случаях не принимать в расчет внутренние силы системы.
Центр масс системы
Когда система состоит из очень большого числа точек, то изучить ее движение сложно и даже иногда невозможно. В таких случаях рассматривается движение всей системы как одного целого. С этой целью и вводится понятие центра масс.
Пусть имеем систему, состоящую из n материальных точек массами ![]() весом
весом ![]() , данная система находится под действием только сил тяжести.
, данная система находится под действием только сил тяжести.
Из курса статики известно, что все эти силы ![]() можно заменить одной силой, приложенной в точке С, называемой центром параллельных сил. Координаты этой точки определяются по формулам:
можно заменить одной силой, приложенной в точке С, называемой центром параллельных сил. Координаты этой точки определяются по формулам:
| (1) |
где Pj = mjg, a xj ,yj , zj — координаты точки Аj.
Заменим Pj в формулах (1) его значением, координаты примут вид
| (2) |
где 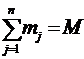 (масса всех точек системы), получим
(масса всех точек системы), получим
| (3) |
Эти формулы (3) определяют точку С, положение которой уже не зависит от сил, действующих на систему, а зависит лишь от положения материальных точек системы и от их масс. Точка С и называется центром масс системы.
Следовательно, центром масс системы называется геометрическая точка С координаты которой определяются по формулам (3).
Итак, центр масс — это точка фиктивная, воображаемая, не связанная ни с какой материальной массой, и вводят это понятие, как уже говорилось, для того, чтобы упростить решение задач динамики системы. Если учесть, что xC , yC , zC — проекции вектора ![]() (радиус-вектора точки С), то можно записать, зная xC , yC , zC :
(радиус-вектора точки С), то можно записать, зная xC , yC , zC :
| (4) |
где ![]() — радиус-вектор точки Аj .
— радиус-вектор точки Аj .
Положение точки С можно определить или ее координатами по формулам (3) или ее радиус-вектором по формуле (4).
Примечание. В поле силы тяжести центр масс системы совпадает с ее центром тяжести (для неизменяемой системы). Но, если центр тяжести существует только для неизменяемой системы, находящейся в поле тяжести, то центр масс существует для любой системы, находящейся в любом пространстве, и положение его не зависит от сил, действующих на систему. Таким образом, понятие центра масс и центра тяжести не являются тождественным понятиями. Центр тяжести является частным случаем по отношению к понятию центра масс.
Момент инерции
Положение центра масс не полностью характеризует распределение масс системы. Поэтому для более полной характеристики распределения масс вводится еще одно понятие — так называемый момент инерции системы, он характеризует распределение масс системы относительно некоторой точки или оси. Впервые это понятие встречается в работах Гюйгенса (1673 г.), но термин и определение момента инерции дано Л. Эйлером (1749 г.).
Моментом инерции системы материальных точек относительно данной точки О (оси Z или плоскости П) называется скалярная величина, равная сумме произведений масс всех точек системы на квадраты их расстояний до данной точки О (оси Z, плоскости П). Обозначая моменты инерции системы относительно точки О![]() , оси Z
, оси Z![]() , плоскости П
, плоскости П![]() , имеем:
, имеем:
| (5) |
где mj — масса точки Аj ; rj , hj , dj — соответствующие расстояния до данной точки О, оси Z, плоскости П.
Чтобы вычислить момент инерции твердого тела относительно данной точки или оси, необходимо разбить тело на очень большое конечное число элементарных частей и определить приближенный момент инерции по формулам (5). Затем, чтобы получить более точное значение момента инерции, нужно вычислить предел приближенного момента инерции, предполагая, что число n частей, на которые разбито тело, стремится к бесконечности, а масса mj каждой части — к нулю.
Например, момент инерции тела относительно точки О 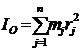 (приближенно), более точно
(приближенно), более точно 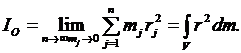
Если тело однородное и имеет правильную геометрическую форму, то его момент инерции можно вычислить с помощью определенного интеграла. Если же тело неоднородное имеет сложную геометрическую форму, то момент инерции его определяется опытным путем.
Значение моментов инерции
Момент инерции относительно различных осей тела необходимо знать при решении многих технических задач. Например, при изучении работы машины или показаний измерительного прибора, при определении степени износа механизма, при динамическом уравновешивании испытуемого тела и т. д.
Осевые, центробежные и полярный момент инерции
 Моменты инерции тела относительно осей координат называются осевыми, а момент инерции тела относительно начала координат — полярным.
Моменты инерции тела относительно осей координат называются осевыми, а момент инерции тела относительно начала координат — полярным.
Вычислим осевые и полярный моменты инерции тела. Пусть имеем твердое тело, разобьем его на отдельные точки и возьмем точку Аj с координатами xj, yj, zj (рис. 3), по определению момента инерции 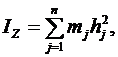 но
но 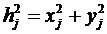 ,
,  тогда
тогда
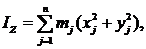 аналогично
аналогично 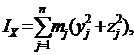 и
и 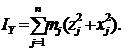
Формулы (6) определят осевые моменты инерции тела:
| (6) |
По определению же найдем полярный момент инерции
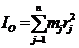 , но
, но ![]() , тогда
, тогда
| (7) |
Осевые и полярные моменты инерции всегда положительны.
Центробежными моментами инерции называются суммы, составленные из произведений масс точек тела на произведение 2 координат этих точек. Центробежные моменты инерции:
| (8) |
Если центробежные моменты инерции относительно некоторой системы осей Oxyz равны нулю, то оси называются главными осями инерции. Для них
IXY = IYZ = IZX = 0.
Главные оси инерции были введены Сегнером (1755 г.) и Эйлером (1758 г.). Через каждую точку пространства можно провести три главные оси инерции данного тела. Главные оси взаимно перпендикулярны. Всякую ось, проходящую через центр масс, называют центральной осью тела. Главные же оси, проходящие через центр масс, называют главными центральными осями инерции тела.
Центробежные моменты инерции в отличие от осевых и полярных моментов могут быть и положительными, и отрицательными.
Примечание. Если однородное тело имеет ось симметрии, то она является его главной центральной осью инерции.
Контрольные вопросы и задания к теме 1
№ 1
От чего зависит положение центра масс?
1. От сил, действующих на систему.
2. От массы системы и от среды, в которой она находится.
3. От масс точек системы и от их расположения.
№ 2
Координаты центра масс системы имеют вид.
1. 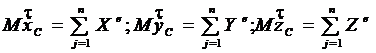 .
.
2. 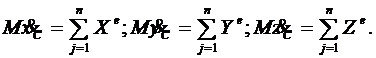 .
.
3. 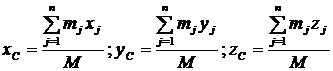 .
.
4. 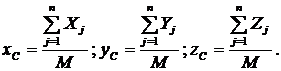
№ 3
Что называется центром масс системы точек?
1. Точка С, положение которой определяется 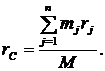
2. Точка С, положение которой вычисляется 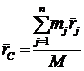 .
.
3. Точка С, положение которой определяется 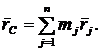
4. Точка С, положение которой находится 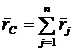 .
.
№ 4
От чего зависит деление сил, действующих на систему, на внешние и внутренние силы?
1. Деление зависит от того, что включается в состав системы.
2. Деление условное, и можно силы, действующие на систему, делить на внутренние и внешние в любом порядке, как угодно.
3. Деление зависит от числа точек, составляющих систему.
4. Деление сил зависит от условия задачи.
№ 5
Какие силы называются внешними?
1. Силы, с которыми действуют друг на друга тела, не входящие в состав одной и той же системы.
2. Силы, приложенные к системе со стороны тел, не входящих в состав самой системы.
3. Силы, для которых главный вектор и главный момент всегда равны нулю.
4. Силы, с которыми действуют друг на друга тела, входящие в состав системы.
№ 6
Свойства внутренних сил.
1. 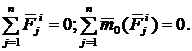
2. 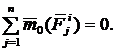
3. 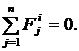
4. 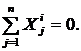
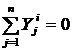 .
.
№ 7
Какие силы называются внутренними?
1. Силы, с которыми действуют друг на друга тела (точки), входящие в состав данной системы.
2. Силы, приложенные к системе со стороны тел, не входящих в состав самой системы.
3. Силы, с которыми действуют друг на друга тела, не входящих в состав одной и той же системы.
4. Внутренние силы — это такие силы, для которых 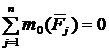 .
.
№ 8
Может ли центр масс системы совпадать с центром тяжести системы?
1. Это два разных понятия.
2. Центр масс только в поле тяготения совпадает с центром тяжести.
3. Центр масс всегда совпадает с центром тяжести.
4. Это зависит от сил, действующих на данную систему. Если внешние силы на систему не действуют, то центр тяжести становится центром масс.
№ 9
По каким формулам определяются моменты инерции твердого тела относительно координатных осей?
1.
| 3.
|
2.
| 4.
|
№ 10
По каким формулам определяются центробежные моменты инерции твердого тела?
1.
| 2.
|
3.
| 4.
|
Тема 2. ТЕОРЕМА О МОМЕНТАХ ИНЕРЦИИ ОТНОСИТЕЛЬНО
ПАРАЛЛЕЛЬНЫХ ОСЕЙ
Этой теоремой пользовался Гюйгенс (1673 г.), общее и строгое доказательство ее дано Л. Эйлером (1749 г.), в литературе она известна как «теорема Гюйгенса», или иногда ее называют «теоремой Штейнера». Штейнер доказал теорему 100 лет спустя (1840 г.) для частного случая (для точек на плоскости). В формулировке Эйлера теорема читается так: момент инерции тела относительно какой-либо оси, равен моменту инерции этого же тела относительно оси ей параллельной, проходящей через центр масс тела, плюс произведение массы тела на квадрат расстояния между осями.
 Доказательство. Пусть имеем некоторое твердое тело, момент инерции которого относительно оси СZ, проходящей через центр масс С тела, известен. Обозначим его через IZ. Необходимо вычислить момент инерции этого же тела относительно оси OZ1, параллельной оси СZ и отстоящей от нее на расстоянии ОС = а (рис. 4).
Доказательство. Пусть имеем некоторое твердое тело, момент инерции которого относительно оси СZ, проходящей через центр масс С тела, известен. Обозначим его через IZ. Необходимо вычислить момент инерции этого же тела относительно оси OZ1, параллельной оси СZ и отстоящей от нее на расстоянии ОС = а (рис. 4).
По определению осевого момента инерции: 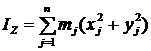 , где mj масса точки Aj. В системе Cxyz xj, yj, zj — ее координаты обозначим: x = xj; y = = yj; z = zj. Теперь опять же по определению осевого момента инерции запишем
, где mj масса точки Aj. В системе Cxyz xj, yj, zj — ее координаты обозначим: x = xj; y = = yj; z = zj. Теперь опять же по определению осевого момента инерции запишем
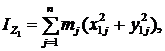
где mj — масса точки Aj; x1j, y1j, z1j – ее координаты в новой системе Ox1y1z1.
Как видим из рис.4, x1j = x; y1j = y – a. Тогда, перейдя к старым координатам, получим
| (1) |
Теорема доказана.
Здесь 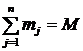 (масса тела).
(масса тела). 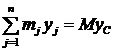 , но С(xC; yC; zC);
, но С(xC; yC; zC);
xC = yC = zC = 0 (C — начало координат);
|
Как видим, 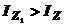 , поэтому можно сделать такой вывод: среди всех моментов инерции относительно различных осей данного направления наименьшее значение имеет момент инерции относительно оси, проходящей через центр тяжести тела.
, поэтому можно сделать такой вывод: среди всех моментов инерции относительно различных осей данного направления наименьшее значение имеет момент инерции относительно оси, проходящей через центр тяжести тела.
Радиус инерции
Очень часто при расчетах пользуются понятием радиуса инерции. Представим себе момент инерции тела относительно оси Z как произведение его массы на квадрат некоторой длины ![]() :
: 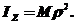
Величину
| (2) |
называют радиусом инерции тела относительно данной оси Z. Радиус инерции ![]() тела можно представить как радиус воображаемого тонкостенного цилиндра, который обладает той же массой, распределенной по его поверхности, и тем же моментом инерции относительно оси, что и данное тело.
тела можно представить как радиус воображаемого тонкостенного цилиндра, который обладает той же массой, распределенной по его поверхности, и тем же моментом инерции относительно оси, что и данное тело.
Вычисления моментов инерции однородных тел
 Пример 1. Определить момент инерции однородного прямолинейного стержня относительно оси, перпендикулярной стержню, проходящей через его конец. Пусть имеем однородный прямолинейный стержень AB = l масса его М, масса единицы длины его
Пример 1. Определить момент инерции однородного прямолинейного стержня относительно оси, перпендикулярной стержню, проходящей через его конец. Пусть имеем однородный прямолинейный стержень AB = l масса его М, масса единицы длины его 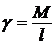 (рис.5), вычислим момент инерции стержня относительно оси Az. Разбиваем стержень на элементарные участки. Возьмем один такой участок длины
(рис.5), вычислим момент инерции стержня относительно оси Az. Разбиваем стержень на элементарные участки. Возьмем один такой участок длины ![]() , масса его
, масса его ![]() . По определению момент инерции
. По определению момент инерции
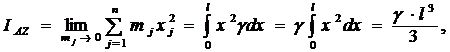 но
но ![]() . Тогда
. Тогда
| ((3) |
Пример 2. Найти момент инерции однородного круглого диска относительно его центра. Пусть имеем однородный круглый диск радиусом R, массой М, масса единицы площади его ![]() (рис. 6). Разобьем диск концентрическими окружностями на элементарные кольца, возьмем одно такое кольцо массой
(рис. 6). Разобьем диск концентрическими окружностями на элементарные кольца, возьмем одно такое кольцо массой ![]() . По определению
. По определению
| (4) |
По формуле (4)считается также момент инерции однородного сплошного круглого цилиндра относительно его оси.
 Пример 3. Найти момент инерции однородного тонкого кольца относительно его центра.
Пример 3. Найти момент инерции однородного тонкого кольца относительно его центра.
Пусть имеем однородное кольцо R, массой М (рис. 7). Момент инерции его относительно центра О по определению момента инерции относительно центра:
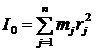 , но
, но ![]() и
и 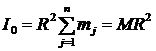 .
.
Получаем:
I0 = MR2. | (5) |
По формуле (5) можно вычислить момент инерции однородного полого цилиндра относительно его оси.
 |
 Используя формулы (3), (4) и теорему о моментах инерции относительно параллельных осей, можно вычислить, например, момент инерции стержня относительно центра тяжести IC или момент инерции диска относительно оси, проходящей через точку А перпендикулярно диску.
Используя формулы (3), (4) и теорему о моментах инерции относительно параллельных осей, можно вычислить, например, момент инерции стержня относительно центра тяжести IC или момент инерции диска относительно оси, проходящей через точку А перпендикулярно диску.
Определим IC (рис. 8).
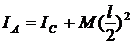 ;
; ![]() ,откуда
,откуда
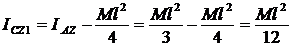 ;
;
| (6) |
Найдем IAZ1 (рис. 9).

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 |




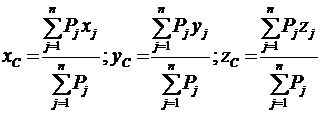 ,
,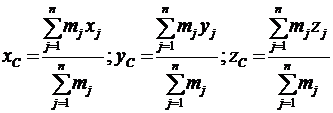 ,
,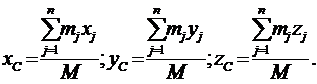
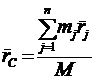 ,
,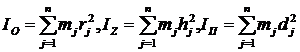 ,
,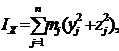
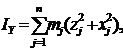
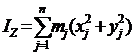 .
.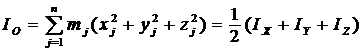 .
.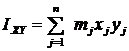 ;
; 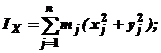
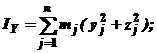
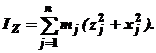
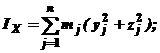
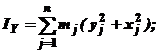
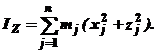
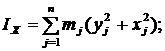
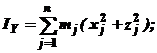
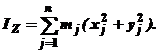
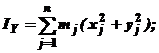
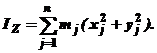
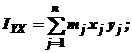
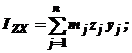
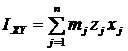 .
.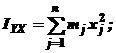
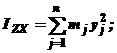
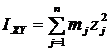 .
.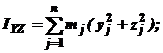
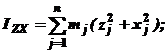
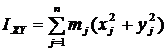 .
.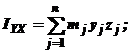
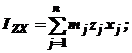
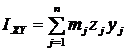 .
.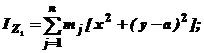
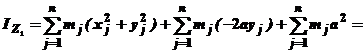
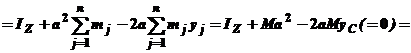
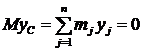 .
.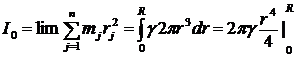 , но
, но 