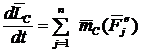1. 
![]() .
.
2. ![]() .
.
3. ![]() .
.
4. ![]() .
.
№ 31
Может ли человек во время прыжка в воду изменить траекторию своего центра тяжести?
1. Не может.
2. Может.
№ 32
Какое условие должно выполнятся, чтобы центр масс не перемещался?
1. 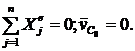
2. 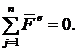
3. 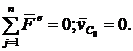
№ 33
Влияют ли внутренние силы на движение центра масс?
1. Да.
2. Нет.
№ 34
Определить главный вектор ![]() внешних сил, приложенных к однородному диску, вращающемуся вокруг неподвижной оси, центр тяжести диска расположен на его оси вращения.
внешних сил, приложенных к однородному диску, вращающемуся вокруг неподвижной оси, центр тяжести диска расположен на его оси вращения.
1. 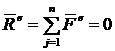 .
.
2. 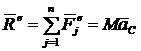 .
.
3. 
![]() .
.
4. Все ответы верны.
№ 35
Какой будет траектория центра масс однородного стержня АВ (рис. 21) при падении его на плоскость? В начальный момент стержень покоился. Плоскость гладкая.
1. Прямая.
2. Окружность.
3. Эллипс.

№ 36
Тонкий однородный стержень ОА = l весом Р вращается вокруг вертикальной оси с постоянной угловой скоростью ![]() (рис. 22). Определить главный вектор внешних сил. Массой оси пренебречь.
(рис. 22). Определить главный вектор внешних сил. Массой оси пренебречь.
1. ![]() .
.
2. ![]() .
.
3. ![]() .
.
№ 37
На однородный цилиндр О, который может свободно вращаться вокруг горизонтальной оси, намотан трос, на свободном конце его подвешен груз А весом Р (рис. 23).
 Определить давление на ось цилиндра, если груз опускается с ускорением а, а вес цилиндра равен Q.
Определить давление на ось цилиндра, если груз опускается с ускорением а, а вес цилиндра равен Q.
1. ![]() .
.
2. ![]() .
.
3. ![]() .
.
4. ![]() .
.
№ 38
Два однородных стержня соединены шарниром С и расположены так, что СД перпендикулярен АВ (рис. 24).
 Определить перемещение стержня АВ, если стержень СД упадет на горизонтальную плоскость. Сопротивления движению не учитывать. Вес стержня АВ — 2Р, стержня СД — Р, АС = ВС = СД = l. В начальный момент система покоилась.
Определить перемещение стержня АВ, если стержень СД упадет на горизонтальную плоскость. Сопротивления движению не учитывать. Вес стержня АВ — 2Р, стержня СД — Р, АС = ВС = СД = l. В начальный момент система покоилась.
1. ![]() .
.
2. Нет верного ответа.
3. ![]()
4. ![]() .
.
№ 39
 Груз весом G поднимается при помощи блочного приспособления (рис. 25).
Груз весом G поднимается при помощи блочного приспособления (рис. 25).
Определить величину реакции оси блока если груз М весом Р опускается с ускорением а. Трением и весом блоков пренебречь.
1. ![]() .
.
2. ![]() .
.
3. ![]() .
.
4.
 |
№ 40
На каком рисунке (26 или 27) верно изображены силы, приложенные к ведущему и ведомому колесам автомобиля?
Тема 4. ТЕОРЕМЫ ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОГО МОМЕНТА
СИСТЕМЫ
Кинетическим моментом системы или главным моментом количеств движения системы относительно некоторого центра О называется вектор ![]() , равный геометрической сумме векторов моментов количеств движения всех точек системы относительно того же центра:
, равный геометрической сумме векторов моментов количеств движения всех точек системы относительно того же центра:
| (1) |
Проекции вектора ![]() на оси Оxyz —
на оси Оxyz —![]() называются кинетическими моментами системы относительно осей координат.
называются кинетическими моментами системы относительно осей координат.
 Кинетическим моментом системы относительно оси называется алгебраическая сумма моментов количеств движения всех точек системы относительно той же оси:
Кинетическим моментом системы относительно оси называется алгебраическая сумма моментов количеств движения всех точек системы относительно той же оси:
| (2) |
Вычислим кинетический момент тела, вращающегося вокруг неподвижной оси Oz с угловой скоростью ![]() (рис. 28).
(рис. 28).
Разобьем тело на отдельные материальные точки и возьмем одну ![]() массой
массой ![]() . Ее расстояние до оси
. Ее расстояние до оси ![]() —
— ![]() , количество движения
, количество движения ![]() . Найдем момент
. Найдем момент ![]() , где
, где ![]() . Тогда
. Тогда 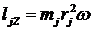 . По определению
. По определению 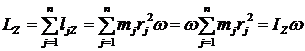 .
.
Итак, | (3) |
Вывод. Кинетический момент вращающегося тела относительно оси вращения равен произведению момента инерции тела относительно этой оси на угловую скорость тела.
Вычислим кинетический момент тела относительно оси С, перпендикулярной к плоскости движения Oхy тела и проходящей через его центр масс С.
Пусть плоская фигура S движется в своей плоскости Охy (рис. 29). Найдем ![]() — кинетический момент фигуры относительно С
— кинетический момент фигуры относительно С 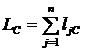 . Найдем
. Найдем  , так как
, так как ![]() , то
, то 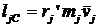 .
.
 |
Тогда
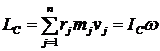 , (8)
, (8)
где ![]()
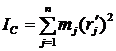 — момент инерции тела относительно оси С.
— момент инерции тела относительно оси С.
Сравнивая выражение (3) и (4), видим, что кинетический момент относительно осей Oz и С одинаков.
Рассмотрим теорему об изменении кинетического момента системы в абсолютном движении.
Пусть имеем систему, состоящую из n точек. Возьмем произвольную точку массой ![]() и запишем для нее теорему об изменении момента количества движения точки в векторной форме
и запишем для нее теорему об изменении момента количества движения точки в векторной форме 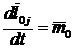 (
(![]() ). Точка взята из системы, значит
). Точка взята из системы, значит![]() и
и 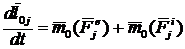 . Подобные равенства напишем для каждой из n точек системы и все их просуммируем. В результат получим
. Подобные равенства напишем для каждой из n точек системы и все их просуммируем. В результат получим 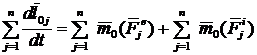 ; по свойству внутренних сил
; по свойству внутренних сил 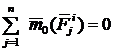 Внесем знак
Внесем знак![]() под знак производной:
под знак производной: 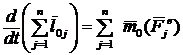 , но
, но 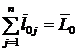 (по определению).
(по определению).
Имеем
| (5) |
Равенство (5) выражает теорему об изменении кинетического момента системы в векторной форме: производная от кинетического момента системы относительно некоторого центра по времени равна сумме моментов всех внешних сил, действующих на систему относительно того центра.
Спроектировав равенство (5) на оси координат, получим
| (6) |
Равенства (6) выражают рассматриваемую теорему в скалярной форме: производная о кинетического момента системы относительно некоторой оси по времени равна сумме моментов всех внешних сил, действующих на систему относительно той же оси.
Частные случаи
1. Если 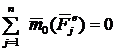 , то
, то 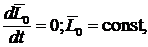 отсюда закон сохранения кинетического момента системы относительно центра О.
отсюда закон сохранения кинетического момента системы относительно центра О.
2. Если 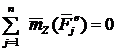 , то
, то 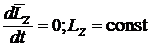 , закон сохранения кинетического момента системы относительно оси z
, закон сохранения кинетического момента системы относительно оси z
Теперь рассмотрим теорему об изменении кинетического момента системы в относительном движении по отношению к центру масс.
 |
Пусть Оxyz — неподвижные оси, относительно которых перемещается система с центром масс С, оси Сx’y’z’ перемещаются поступательно вместе с центром масс С системы (рис. 30), при этом оси Cx’y’z’ имеют ускорение
Изучая динамику относительного движения, выяснили, что в инерциальных осях Cx’y’z’ все уравнения динамики можно составлять так же, как и в неподвижных осях, если к действующим на каждую точку Aj системы силам ![]() и
и ![]() прибавить переносную силу инерции
прибавить переносную силу инерции ![]() и кориолисову силу инерции
и кориолисову силу инерции ![]() . В данном случае переносное движение осей Cx’y’z’ поступательное и
. В данном случае переносное движение осей Cx’y’z’ поступательное и ![]() , а
, а ![]() . Уравнение (5) в осях Cx’y’z’ примет вид
. Уравнение (5) в осях Cx’y’z’ примет вид
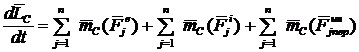 . (7)
. (7)
Но по свойству внутренних сил 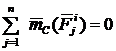 . По определению кинетического момента системы
. По определению кинетического момента системы 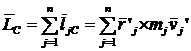 ,
,
где ![]() — скорость
— скорость ![]() в подвижной системе Cx’y’z’.
в подвижной системе Cx’y’z’.
Вычислим 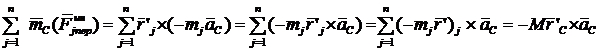 .
.
Но точка С есть начало координатных осей Cx’y’z’. Поэтому 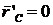 и
и ![]() . Тогда
. Тогда 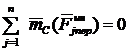 .
.
Теперь уравнение (7) примет вид
| (8) |
Сравнивая этот результат с уравнением (5), видим, что для осей, движущихся поступательно вместе с центром масс системы, теорема об изменении кинетического момента системы относительно центра масс сохраняет тот же вид, что и относительно неподвижного центра.
Пример 1. Груз В весом P1 поднимается при помощи ворота силой G (рис. 31). Вес барабана ворота P2 радиус барабана R, длина рукоятки ОА = l. Определить ускорение груза В. Барабан считать сплошным однородным цилиндром.
Система состоит из груза, нити, барабана с рукояткой. На данную систему действуют внешние силы: ![]()
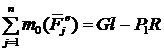 . По теореме об изменении кинетического момента системы
. По теореме об изменении кинетического момента системы
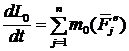 . Найдем
. Найдем 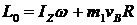 . Заменим
. Заменим ![]() , получим
, получим 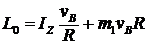 . Дифференцируя
. Дифференцируя ![]() , находим, что
, находим, что
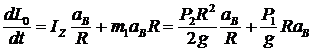 . Но
. Но 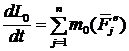 .
.
Тогда 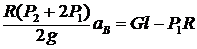 откуда
откуда ![]() .
.
Порядок решения задач с помощью теоремы об изменении кинетического
момента системы
1. Направить одну из осей координат вдоль неподвижной оси вращения z.
2. Записать теорему об изменении главного момента количеств движения системы относительно соответствующей оси: 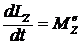 .
.
3. Изобразить на рисунке все внешние силы системы.
4. Вычислить главный момент внешних сил относительно неподвижной оси z
5. Вычислить кинетический момент системы относительно оси z, затем взять его производную по времени.
6. Подставить результаты пп.4 и 5 в п.2 и затем, в зависимости от условия, решить прямую либо обратную задачу динамики.
Последовательность решения задач с помощью закона сохранения
кинетического момента системы
1. Выбрать координатные оси, направив одну из них вдоль неподвижной оси вращения.
2. Записать теорему об изменении кинетического момента системы материальных точек относительно выбранной оси, например, 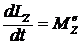 .
.
3. Изобразить на рисунке все внешние силы системы.
4. Показать, что сумма моментов всех внешних сил системы относительно оси z равна нулю.
5. Вычислить и приравнять кинетические моменты системы материальных точек относительно оси z в начальный и конечный момент времени: ![]() .
.
6. Решить уравнение 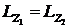 , определить искомую величину.
, определить искомую величину.
Пример 2. Однородный диск массой ![]() и радиусом r вращается вокруг оси АВ с угловой скоростью
и радиусом r вращается вокруг оси АВ с угловой скоростью ![]() (рис. 32). По радиусу диска движется точка М массой
(рис. 32). По радиусу диска движется точка М массой ![]() с постоянной скоростью
с постоянной скоростью ![]() . Определить угловую скорость диска в момент t.
. Определить угловую скорость диска в момент t.
Система состоит из диска, точки, оси. На нее действуют внешние силы: веса ![]() ,
, 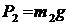 и реакции опор А и В, найдем
и реакции опор А и В, найдем 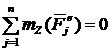 , так как
, так как ![]() и
и ![]() параллельны Az, а реакции опор А и В пересекают ось Az.
параллельны Az, а реакции опор А и В пересекают ось Az.
 Тогда
Тогда 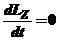 ,
, ![]() .
.
Найдем 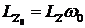 ,
, ![]() . Но
. Но 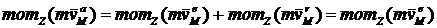 .
. ![]() , так как
, так как ![]() пересекает Az, а
пересекает Az, а 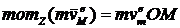 .
.
Подставив значение 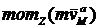 , получим
, получим
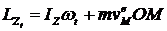 , но
, но ![]() ;
; 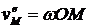 , а
, а ![]() .
.
Тогда 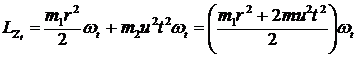 , но
, но 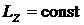 и поэтому
и поэтому ![]() , приравнивая
, приравнивая 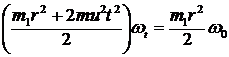 ,
,
получаем 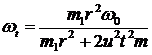 .
.
Контрольные вопросы и задания к теме 4
№ 41
Может ли танцор во время прыжка в танце изменять угловую скорость вокруг оси, проходящей через центр тяжести его?
1. Да.
2. Не может.
№ 42
Два человека весом Р каждый стоят на концах горизонтального стержня АВ с тем же весом, вращающегося вокруг вертикальной оси О, проходящей через середину стержня, с угловой скоростью ![]() .
.
Как изменится угловая скорость, если оба человека займут положение на серединах отрезков ОА и ОВ?
1. ![]() , не изменится угловая скорость.
, не изменится угловая скорость.
2. ![]() , стержень остановится.
, стержень остановится.
3. ![]()
![]() , угловая скорость станет меньше.
, угловая скорость станет меньше.
4. ![]() , угловая скорость станет больше.
, угловая скорость станет больше.
№ 43
Определить кинетический момент данной системы относительно оси z. Точки 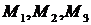 лежат в плоскости Оxy (рис. 33).
лежат в плоскости Оxy (рис. 33).
 1.
1.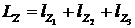 .
.
2.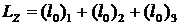 .
.
3. ![]() .
.
4. ![]() .
.
Выберете неверный ответ.
№ 44
Которое утверждение верно?
1. ![]() , если
, если 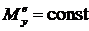 .
.
2. ![]() , если
, если 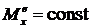 .
.
3. ![]() , если
, если 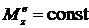 .
.
4. ![]() , если
, если 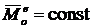 (
(![]() ).
).
№ 45
Которое утверждение неверное?
1. Производная от кинетического момента системы относительно центра О по времени равна скорости конца вектора кинетического момента.
2. Скорость конца вектора кинетического момента системы относительно центра О равна главному моменту внешних сил относительно того же центра.
3. Производная от кинетического момента системы относительно центра О по времени равна главному моменту внешних сил относительно того же центра.
4.  Производная от кинетического момента системы относительно центра О по времени равна главному моменту внешних сил относительно оси Oz, проходящей через центр О.
Производная от кинетического момента системы относительно центра О по времени равна главному моменту внешних сил относительно оси Oz, проходящей через центр О.
№ 46
Стержень АВ = l весом Р с прикрепленными на концах шариками весом Q каждый вращается вокруг вертикальной оси с угловой скоростью ![]() (рис. 34).
(рис. 34).
Какова станет его угловая скорость, если шарик упадут вниз по стержням АС и ВС в точку С?
1. ![]() .
.
2. ![]() .
.
3. ![]() .
.
№ 47
 Ротор А находится в покое. Внезапно к нему присоединили с помощью муфты С ротор В, имеющий начальную скорость
Ротор А находится в покое. Внезапно к нему присоединили с помощью муфты С ротор В, имеющий начальную скорость ![]() (рис. 35). Какова общая угловая скорость двух систем, если момент инерции системы А равен
(рис. 35). Какова общая угловая скорость двух систем, если момент инерции системы А равен ![]() , а система В —
, а система В — ![]() ?
?
1. ![]() .
.
2. ![]() .
.
3. ![]() .
.
№ 48
Деревянная доска длиной l и весом P может вращаться без трения вокруг горизонтальной оси OO1. В середину доски углубляется пуля, летевшая перпендикулярно доске со скоростью V0 (рис. 36). Определить угловую скорость, которую приобретает доска в момент попадания пули, если вес пули P1.
1. .
2. ![]() .
.
3. 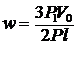 .
.
4. .
№ 49
Определить кинетический момент системы, состоящей из трех точек, относительно центра О. Точки расположены в пространстве произвольно.
1. 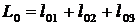 .
.
2. 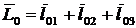 .
.
3. 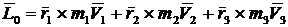 .
.
Укажите неверный ответ.
№ 50
Однородный цилиндр радиусом r и весом P может свободно вращаться вокруг неподвижной оси АВ. На цилиндр намотан нерастяжимый трос, к концам которого прикреплены грузы M1 и M2 весом P1 и P2 (P2 >P1) (рис. 37). Определить угловое ускорение цилиндра.
1. .
2. .
3. .
4. .
Тема 5. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ
СИСТЕМЫ
Кинетическая энергия системы T равна сумме кинетических энергий всех точек системы, т. е.
(1)
Рассмотрим кинетическую энергию твердого тела.
Поступательное движение тела
При поступательном движении тела скорости всех точек его в любой момент времени одинаковы. Общую скорость обозначим через скорость центра масс . Тогда, разбив тело на отдельные материальные точки, вычислим его энергию по формуле
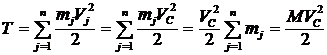 .
.
Итак, , (2)
где М — масса тела.
Вывод. Кинетическая энергия тела в поступательном движении равна половине произведения массы тела на квадрат скорости его центра масс.
Вращательное движение тела
Вычислим кинетическую энергию тела, вращающегося вокруг неподвижной оси с угловой скоростью ω (рис. 38). Для этого разобьем тело на отдельные материальные точки. Энергия каждой точки равна , а для всего тела как для системы 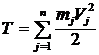 ,
,
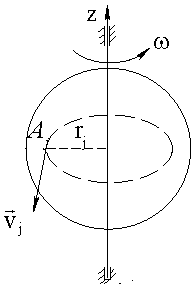 где Vj — скорость любой точки Aj тела, определяется по формуле . Тогда
где Vj — скорость любой точки Aj тела, определяется по формуле . Тогда
;
где — момент инерции тела относительно оси вращения.
. (3)
Вывод. Кинетическая энергия вращающегося твердого тела равна половине произведения момента инерции тела относительно оси вращения на квадрат его угловой скорости.
Плоскопараллельное движение тела
Из кинематики известно, что скорости всех точек плоской фигуры S (рис. 39) относительно мгновенного центра скоростей P распределяется так, как будто эта фигура вращается вокруг оси, перпендикулярной плоскости фигуры и проходящей через мгновенный центр скоростей P. Следовательно, энергию этой фигуры можно вычислить, как энергию вращающегося тела:
(4)
Но положение центра скоростей с течением времени меняется относительно движущейся фигуры, следовательно, меняется и момент инерции I, поэтому полученная формула неудобна для практики. Преобразуем ее, используя теорему о моментах инерции относительно параллельных осей. Заменим . Имеем
,
где (по свойствам плоского движения).
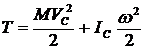 . (5)
. (5)
Вывод. Кинетическая энергия тела при плоскопараллельном движении его равна сумме двух энергий: энергии этого тела в поступательном движении со скоростью центра масс и энергии его во вращательном движении вокруг оси, проходящей через центр масс.
Рассмотрим теорему об изменении кинетической энергии системы.
Пусть имеем систему, состоящую из n материальных точек. Возьмем из этой системы некоторую точку Aj и запишем для нее теорему об изменении кинетической энергии точки в дифференциальной форме:
,
где dAе — элементарная работа внешних сил; dAi — внутренних сил.
Запишем подобные равенства для каждой из п точек системы и все их просуммируем. Имеем .
Внесем знак суммы под знак дифференциала: 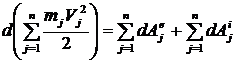 .
.
Здесь ,
окончательно . (6)
Полученное равенство выражает теорему об изменении кинетической энергии системы в дифференциальной форме: дифференциал кинетической энергии системы равен сумме элементарных работ всех внешних и внутренних сил, действующих на систему.
Проинтегрируем равенство (6), получим
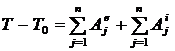 . (7)
. (7)
Та же теорема в интегральной форме: изменение кинетической энергии системы при конечном перемещении ее из одного положения в другое равно сумме работ на этом перемещении всех внешних и внутренних сил, действующих на систему.
В случае неизменяемой системы теорема примет вид
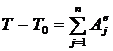 . (8)
. (8)
Здесь 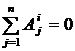 . (9)
. (9)
Пример. На шкив радиусом R, весом Р намотана веревка, к концу которой подвешен груз весом Q (рис. 40). В начальный момент система покоилась. Найти угловую скорость шкива в тот момент, когда груз опустился на высоту h. Массу шкива считать равномерно распределенной по ободу. Трением пренебречь.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 |




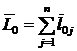
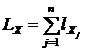 ;
; 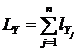 ;
; 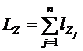
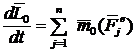 .
.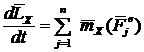 ;
; 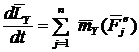 ;
; 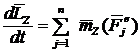 .
.