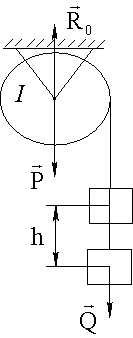
 Данная система состоит из вращающегося шкива и груза, который движется поступательно. Энергия системы
Данная система состоит из вращающегося шкива и груза, который движется поступательно. Энергия системы
;
,
где ; ; .
На основании теоремы об изменении кинетической энергии
, но Т0 = 0; .
Тогда ; , поэтому имеем
![]() .
.
Здесь Т0 = 0 (по условию); (система неизменяемая, так как тела абсолютно твердые, веревка нерастяжима).
Откуда .
Решение задач с помощью теоремы об изменении кинетической энергии в интегральной форме рекомендуется проводить в такой последовательности:
1) изобразить на рисунке все внешние и внутренние силы системы (в случае неизменяемой материальной системы — только внешние силы);
2) вычислить сумму работ всех внешних и внутренних сил на перемещениях точек системы (в случае неизменяемой материальной системы — только сумму работ внешних сил);
3) вычислить кинетическую энергию системы материальных точек в начальном и конечном положениях системы;
4) воспользовавшись результатами вычислений 2 и 3, записать теорему об изменении кинетической энергии системы материальных точек:
или в случае неизменяемой системы по формуле
и определить искомую величину.
Контрольные вопросы и задания к теме 5
№ 51
Чему равна кинетическая энергия звена АВ кривошипно-шатунного механизма в тот момент, когда кривошип ОА занимает правое горизонтальное положение (рис. 41), если OA = r; AB = l; ωOA = ω0; AC = CB; mAB = M (OA и AB — однородные стержни)?
1. .
2. .
3. .
Укажите неверный ответ.
№ 52
Определить кинетическую энергию кулисы O1B = l массой т, если кривошип ОА вращается с угловой скоростью ω0 и OA = r; O1C = CB (рис. 42).
1. ![]() .
.
2. ![]() .
.
3. ![]() .
.
4. ![]() .
.
Выбрать неверный ответ и выразить через данные величины.
№ 53
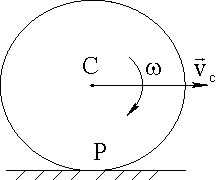
Чему равна кинетическая энергия диска, катящегося по неподвижной плоскости без скольжения (рис. 43) со скоростью VC ?
 1. ;
1. ; 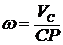 .
.
2. ![]() .
.
3. ![]() .
.
Укажите неверный ответ.
№ 54
Кривошип ОА вращается с угловой скоростью ω0 (рис. 44): OA = r; AB = l; MAB = M. Чему равна кинетическая энергия шатуна АВ в указанном на чертеже положении?
1. ![]() .
.
2. ![]() .
.
3. ![]() .
.
Здесь М — масса шатуна;
IC — момент инерции шатуна относительно точки С.
Укажите неверный ответ.
№ 55
 Цилиндр массой М может перемещаться по неподвижной плоскости (рис. 45). Чему равна его кинетическая энергия?
Цилиндр массой М может перемещаться по неподвижной плоскости (рис. 45). Чему равна его кинетическая энергия?
1. ![]() .
.
2. ![]() .
.
3. ![]() .
.
№ 56
Две материальные точки А и В массой т каждая прикреплены к твердому невесомому стержню длиной 2а м, имеющему неподвижную точку О, одна на конце, другая на середине стержня (рис. 46).
 В начальный момент стержень отклонен на 60о от вертикали и предоставлен самому себе. Найти угловую скорость w, с которой стержень пройдет через положение равновесия.
В начальный момент стержень отклонен на 60о от вертикали и предоставлен самому себе. Найти угловую скорость w, с которой стержень пройдет через положение равновесия.
1. ![]() .
.
2. ![]() .
.
3. ![]() .
.
4. ![]() .
.
№ 57
Система состоит из двух точек массой т каждая, они движутся по прямой навстречу друг другу с одинаковыми скоростями V. Чему равна кинетическая энергия системы?
1. ![]() .
.
2.
3.
4. Нет верного ответа.
№ 58
Однородный диск в одном случае вращается вокруг неподвижной оси, перпендикулярной его плоскости и проходящей через центр, а в другом катится без скольжения по прямой. Угловая скорость диска в обоих случаях одинакова. Когда кинетическая энергия больше и во сколько раз?
1. В 2 раза больше при качении.
2. В 3 раза больше при качении.
3. Одинакова.
4. Нет верного ответа.
№ 59
Круглая шайба радиусом R весом P вращается в вертикальной плоскости вокруг неподвижной точки О с угловой скоростью ω (рис. 47) OC = R. Найти кинетическую энергию шайбы.
1. 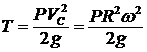 .
.
 2.
2. ![]() .
.
3. ![]() .
.
4. ![]() .
.
№ 60
Сплошной цилиндр скользит по плоскости со скоростью VC . Изменится ли его кинетическая энергия, если цилиндр катить по плоскости с той же скоростью оси VC (рис. 48)? Насколько изменится энергия?
1. Не изменится, 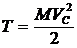 .
.
2. Изменится, увеличится на ![]() .
.
3. Изменится, уменьшится на
4. Изменится, увеличится на ![]() .
.
№ 61
Вал весом P и радиусом инерции r делает n оборотов в минуту. От трения в подшипниках число оборотов уменьшилось наполовину. Какую энергию поглотило трение?
1. ![]() .
.
2. ![]() .
.
3. ![]() .
.
4. ![]() .
.
№ 62
Колесо скатывается без скольжения по наклонной плоскости с высоты h. Какую скорость приобретает центр колеса, если начальная скорость центра равна нулю?
1. ![]() .
.
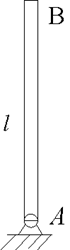 2.
2. ![]() .
.
3. ![]() .
.
№ 63
Какую надо сообщить угловую скорость ω0 стержню АВ в его верхнем положении, чтобы он проходил через нижнее положение с угловой скоростью 2ω0 (рис. 49)?
1. ![]() .
.
2. ![]() .
.
3. Нет верного ответа.
№ 64
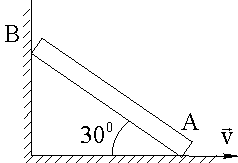
Однородный стержень AB = l весом P скользит своими концами по горизонтальной и вертикальной плоскости (рис. 50). Найти кинетическую энергию стержня в указанном на чертеже положении, если скорость точки A VA = V.
 1.
1. ![]() .
.
2. ![]() .
.
3. ![]() .
.
4. ![]() .
.
ОТВЕТЫ И РЕШЕНИЯ К КОНТРОЛЬНЫМ ВОПРОСАМ
№ 1
Центр масс системы — это геометрическая точка, положение которой определяется координатами или радиус-вектором:
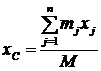 ;
; 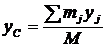 ; ; ( или ).
; ; ( или ).
Из формул видно, что положение центра масс не зависит от сил, действующих на систему, а значит и от среды, а зависит от масс точек системы и от расположения их (т. е. от координат xj, yj, zj и от mj). Верен ответ 3. Остальные ответы не верны.
№ 2
Смотрите ответ к № 1. Верен ответ 3.
№ 3
Смотрите ответ к № 1. Верен ответ 2.
№ 4
Верен ответ 1.
№ 5
Верен ответ 2.
№ 6
Верен ответ 1.
№ 7
Верен ответ 1.
№ 8
Верен ответ 2.
№ 9, № 10
Верны ответы 4.
Пояснения к № 4–10 найдите в тексте темы 1.
№ 11
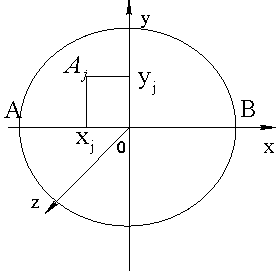 Чтобы вычислить момент инерции диска относительно диаметра АВ, построим оси координат с началом в центре диска. Ось ОХ направим по диаметру АВ, ОУ — перпендикулярно АВ, а ось OZ перпендикулярно плоскости диска (рис. 53), при этом знаем, что
Чтобы вычислить момент инерции диска относительно диаметра АВ, построим оси координат с началом в центре диска. Ось ОХ направим по диаметру АВ, ОУ — перпендикулярно АВ, а ось OZ перпендикулярно плоскости диска (рис. 53), при этом знаем, что 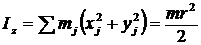 ;
; ![]() ;
; 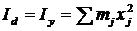 ;
; ![]() ,
,
так как 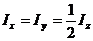 ;
; ![]() .
.
Верен ответ 2.
Ответ 1. .
Ответ 4. Взято Iz для тонкого кольца, равное mr2, вместо Id диска.
Ответ 3. относительно оси, проходящей через конец прямолинейного однородного стержня, перпендикулярно ему. Эти ответы неверны.
№ 12
Проводим через C ось l || l1 (рис. 51). Момент инерции диска относительно оси, проходящей вдоль диаметра:
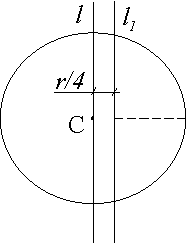
![]() ,
,
тогда 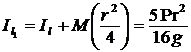 .
.
Верен ответ 4.
В ответе 1 взято равным .
В ответе 2 взято равным .
В ответе 3 взято равным Il.
Ответы 1–3 неверны.
№ 13
Смотрите ответ к задаче № 11, так как , а .
Верен ответ 4, остальные неверны, так как неверен .
№ 14
Ответ 1 неверен. Радиус инерции цилиндра и радиус цилиндра — это не одно и то же (рис. 52). Чтобы найти , воспользуемся формулами:
; ; .
Верен ответ 2.
Ответ 3 неверен. Вместо записан Iz.
№ 15
Чтобы вычислить Iz (рис. 54), воспользуемся теоремой о моментах инерции относительно параллельных осей. Моменты инерции диска относительно каждого из его диаметров одинаковы.
Выберем диаметр АВ, параллельный касательной : .
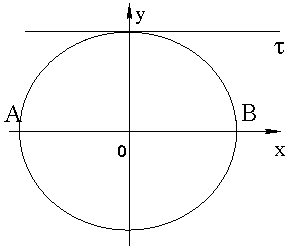 Тогда
Тогда ![]() .
.
Верен ответ 2. Остальные ответы неверны.
Ответ 1. (относительно центра О).
Ответ 3: (относительно диаметров).
Опустив значок около I, обозначающий ось, относительно которой считается момент инерции, допускаете грубую ошибку. Не забывайте обозначать ось, относительно которой считаете момент инерции. Ответ 4: (для кольца).
№ 16
Ответ 1 неверен. Это запись момента инерции стержня относительно оси AZ: (рис. 55). Находим .
 Верен ответ 3. Ответ 2 неверен, ошиблись в расчете.
Верен ответ 3. Ответ 2 неверен, ошиблись в расчете.
№ 17
Верен ответ 1. Вычислим момент инерции пластинки относительно оси Oz (рис. 56). Для этого площадь прямоугольника ОАВС разобьем прямыми, параллельными оси Оу, на бесконечно узкие полоски. Будем рассматривать каждую полоску как прямолинейный отрезок массы mj. Тогда момент инерции полоски относительно оси Oz будет равен , по формуле (3) темы 2. Тогда 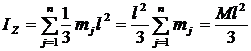 .
.
Используя теорему о моментах инерции относительно параллельных осей, имеем 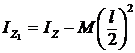 ;
; 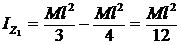 .
.
Верен ответ 1. Остальные ответы неверны.
№18
Разобьем стержень на п элементарных частиц (рис. 57). Возьмем одну такую частицу Aj,ее масса mj, расстояние AjС = lj. Тогда , так как , то , но
.
Подставим значение IC в формулу, полученную для IZ:
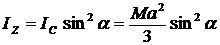 .
.
Верен ответ 1.
Ответ 2. Ошибка в счете .
В ответах 3, 4 неверно взята длина: АВ = а вместо 2а. Поэтому и . В ответе 4 к тому же вместо взято .
№ 19
Верен ответ 1. Найдем Iy. Для этого разобьем прямоугольник прямыми, параллельными оси у, на бесконечно узкие полоски (рис. 58). Будем рассматривать каждую полоску как прямолинейный отрезок массы mj. Тогда по формуле (3) темы 2 момент инерции полоски относительно Оу будет равен , а момент инерции всего прямоугольника 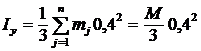 ,
,
где — масса прямоугольника.
Теперь из формулы (1) темы 2 найдем ![]() ,
,
но м.
В ответе 2 вместо взят Iy и поэтому 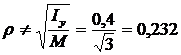 м.
м.
Ответ 2 неверен. В ответе 3 неверно применяется формула (1) темы 2:
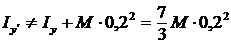 и
и ![]() м.
м.
№ 20
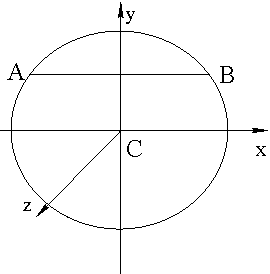 Верен ответ 3. Момент инерции круга относительно диаметра (оси Оx, рис. 59) равен (см. ответ к № 14). По теореме о моментах инерции относительно параллельных осей:
Верен ответ 3. Момент инерции круга относительно диаметра (оси Оx, рис. 59) равен (см. ответ к № 14). По теореме о моментах инерции относительно параллельных осей:
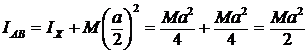 .
.
В ответе 1 вместо IX взят , кроме того, неверно применена теорема о моментах инерции относительно параллельных осей:
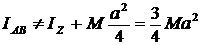 ,
,
так как АВ непараллельна Oz. В ответе 2 вместо IAB взят IX, что тоже неверно.
№ 21
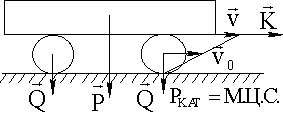 Рассмотрим движение системы, состоящей из бревна, которое движется поступательно, и двух катков, совершающих плоскопараллельное движение (рис. 60).
Рассмотрим движение системы, состоящей из бревна, которое движется поступательно, и двух катков, совершающих плоскопараллельное движение (рис. 60).
Количество движения этой системы ; выразим через скорость центра масс , что видно из распределения скоростей точек катка (см. рис. 60): ; ; ![]() .
.
Верен ответ 3. Ответы 1 и 2 неверны. В 1-м ответе неверно считается Q общей массой двух катков, а во втором случае V0 приравнивается V, забывая, что у центра катка скорость 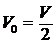 .
.
№ 22
Рассмотрим движение системы, состоящей из двух точек А и В и стержня АВ (рис. 61). Количество движения этой системы
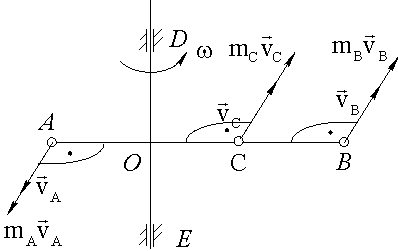
![]() ;
; 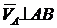 ; ; ; ; ; n = 10 oб/мин;
; ; ; ; ; n = 10 oб/мин;
![]() с–1;
с–1; 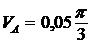
![]() ;
; 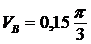
![]() ;
; 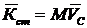 ;
;
![]() ; ; , так как ; кгм/с. .
; ; , так как ; кгм/с. .
Верен ответ 2.
Ответ 1 неверен, так как не соблюдается система единиц, см не переведены в м, а g взято 9,8 м/с2 вместо 980 см/с2. Ответ 3 тоже неверен, так как вектор направлен в противоположную сторону векторам и и его следует вычесть из суммы 2 остальных , а вы сложили, не учтя направления .
№ 23
Ответ 1 неверный. , но в относительном движении диска вокруг оси ВС (рис. 62), так как центр диска лежит на этой оси. Тогда ![]()
К = К1 + К2; 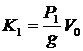 ;
;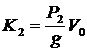 ;
; 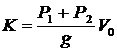 ;
; 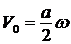 ;
; 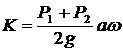 ;
; 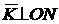 .
.
Верен ответ 2. Ответ 3 неверен: . Ответ 4 неверен: .
№ 24
Рассмотрим движение системы лодка — человек (рис. 63). Запишем для этой системы теорему об изменении количества движения системы в проекции на ось х в интегральной форме .
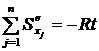 ; ;
; ;
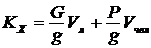 ;
; ![]() ;
;
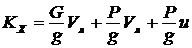 ;
; ![]() .
.
При Vл = 0 ; 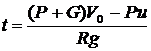 .
.
Верен ответ 1. В ответе 2 неверно вычислена проекция импульса ![]() :
:
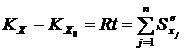 ;
; ![]() ;
;
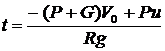 .
.
№ 25
Применяем теорему об изменении количества движения системы в проекции на ось х. Но так как Reх = 0, то .
; ;
приравнивая ![]() и
и ![]() :
: ![]() ;
; 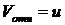 , имеем
, имеем
![]() .
.
Верен ответ 3.
В ответе 1 неверно вычислена скорость человека: 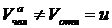 ;
;
![]() ;
; 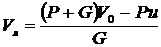 .
.
В ответе 2 КХ вычислено верно. Но 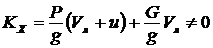 , так как
, так как ![]() . Тогда
. Тогда 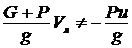 ;
; ![]() .
.
№ 26
Количество движения системы (рис. 64)
![]() ;
; 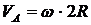 ;
; ![]() . Так как
. Так как 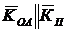 то
то

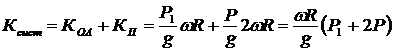 .
.
Верен ответ 3. Ответ 1 неверен.
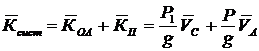 ,
,
но ![]() , так как
, так как 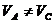 .
.
Ответ 2 неверен, перепутаны VA и VC .
![]() и
и 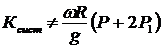 .
.
№ 27
Верен ответ 3. Система состоит из двух точек А и В (рис. 65).
![]() ;
; 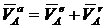 ;
; ![]() ;
; 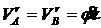 ;
; ![]() ;
; 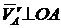 ;
; ![]() ;
; ![]() ;
; ![]() и
и 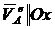 ;
; ![]() .
.
Стержни ОА и ОВ лежат в плоскости Оyz и проекции их скоростей
![]() ;
; 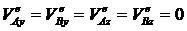 ;
; ![]() ;
;
![]() ;
;
![]() ;
;
![]() .
. 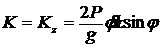 .
.
Остальные ответы неверны. В первом ответе 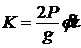 — количество движения только в относительном движении шаров. Векторы
— количество движения только в относительном движении шаров. Векторы ![]() , неверно складываются.
, неверно складываются.
Во втором ответе ![]() считается только в переносном движении и тоже неверно считается сумма векторов
считается только в переносном движении и тоже неверно считается сумма векторов  .
.
В четвертом ответе ошибка в проекции, 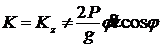 .
.
№ 28
Система состоит из двух колес (рис. 66).
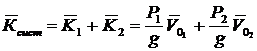 , но
, но 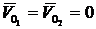 ;
; ![]() .
.
Верен ответ 1. Остальные ответы неверны: в ответе 2 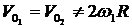 ;
; 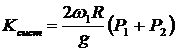 ; в ответе 3
; в ответе 3 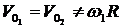 ;
; 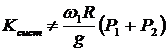 .
.
№ 29
 Система состоит из двух точек М1 и М2 и стержня (рис. 67). Стержень невесомый
Система состоит из двух точек М1 и М2 и стержня (рис. 67). Стержень невесомый ![]() ;
; 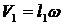 ;
; ![]() ;
; 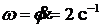 , так как ; то
, так как ; то ![]() . Верен ответ 2.
. Верен ответ 2.
Ответ 1 неверен, так как ![]() . Ответ 3 неверен, так как и направлены в одну сторону
. Ответ 3 неверен, так как и направлены в одну сторону ![]() .
.
№ 30
Верен ответ 4. 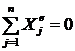 (рис. 68);
(рис. 68); 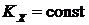 ;
; ![]() .
. 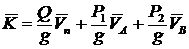 .
.
![]() ;
; 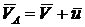 ;
; ![]() ;
;
![]() .
.
![]() ;
; 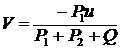 .
.
Знак минус говорит о том, что параллелепипед будет перемещаться в сторону, противоположную перемещению груза А относительно параллелепипеда.
 |
В ответе 1 неверно считаются скорости.
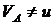 и
и 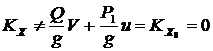 ;
; 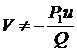 .
.
В ответе 2, как и в первом ответе 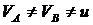 и
и ![]() считается неверно, так как
считается неверно, так как ![]() .
. 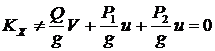 ;
; 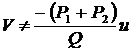 .
.
В ответе 3 КХ найдено неверно.
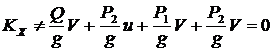 ;
;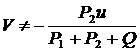 .
.
№ 31
Не может. На человека (точку М), прыгающего в воду (рис. 69), кроме силы тяжести, никакие внешние силы не действуют, поэтому 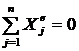 ;
; ![]() , так как
, так как 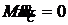 ;
; ![]() ;
; 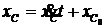 ;
; 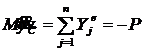 ;
; 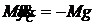 ;
; ![]() ;
; 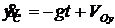 ;
; ![]() .
.
Уравнения движения данной точки: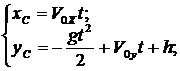
Исключая переменную t, найдем 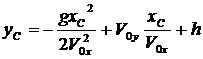 — уравнение параболы. Траекторией прыгуна будет парабола при любой скорости
— уравнение параболы. Траекторией прыгуна будет парабола при любой скорости ![]() . Под действием силы тяжести точка всегда перемещается только по параболе, т. е. траектории своей прыгун изменить не может.
. Под действием силы тяжести точка всегда перемещается только по параболе, т. е. траектории своей прыгун изменить не может.
№ 32
Теорема о движении центра масс говорит о том, что центр масс системы движется согласно закона 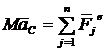 , или
, или 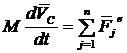 . Если
. Если 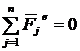 , то
, то 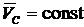 ; если
; если ![]() , то
, то 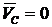 .
.
Верен ответ 3. Ответ 2 неполный. Ответ 1 предполагает отсутствие перемещения центра масс только вдоль оси х.
№ 33
Верен ответ 2. Внутренние силы не влияют на движение центра масс, потому что его движение происходит согласно равенства 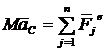 , куда внутренние силы не входят.
, куда внутренние силы не входят.
№ 34
Верен ответ 1, так как ускорение центра масс ![]() , лежащего на оси вращения, равно нулю, то и
, лежащего на оси вращения, равно нулю, то и 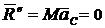 . То же самое получим в ответе 2, если вместо аС подставим значение и в ответе 3 положим rC = 0 для точек, расположенных на оси вращения. Эти ответы верны тоже. Поэтому следует считать верным заключение, выраженное ответом 4.
. То же самое получим в ответе 2, если вместо аС подставим значение и в ответе 3 положим rC = 0 для точек, расположенных на оси вращения. Эти ответы верны тоже. Поэтому следует считать верным заключение, выраженное ответом 4.
№ 35
 Так как на стержень АВ (рис. 70) никакие силы кроме веса Р и нормальной реакции N, не действуют, а их проекции на ось х равны 0 и стержень в начальный момент неподвижен, то
Так как на стержень АВ (рис. 70) никакие силы кроме веса Р и нормальной реакции N, не действуют, а их проекции на ось х равны 0 и стержень в начальный момент неподвижен, то 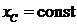 . Для выполнения этого условия (
. Для выполнения этого условия (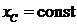 ) необходимо, чтобы точка С перемещалась только по прямой, параллельной оси Ау. Верен ответ 1.
) необходимо, чтобы точка С перемещалась только по прямой, параллельной оси Ау. Верен ответ 1.
№ 36
Верен ответ 1. На основании теоремы о движении центра масс

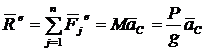 .
.
Найдем ![]() (так как вращение стержня (рис. 71) равномерное):
(так как вращение стержня (рис. 71) равномерное):
![]() ;
;
![]() .
.
Направлен ![]() , как и от С к О. Но
, как и от С к О. Но 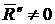 , так как
, так как ![]() ;
; 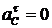 .
.
Ответ 2 неверен. Ответ 3 неверен, так как 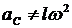 ;
; ![]() .
.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 |




