№ 37
Для решения задачи используем дифференциальное уравнение движения центра масс: 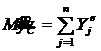 ;
; 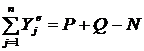 (рис. 72).
(рис. 72). ![]() ;
; 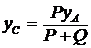 ;
; ![]() ;
; 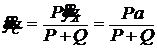 ;
; ![]() ;
; 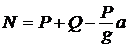 .
.
 Верен ответ 4. В ответах 2 и 3 неверно найдена сумма проекций сил на ось у. В ответе 1 не учитывается движение системы, сила N найдена в равновесном положении.
Верен ответ 4. В ответах 2 и 3 неверно найдена сумма проекций сил на ось у. В ответе 1 не учитывается движение системы, сила N найдена в равновесном положении.
№ 38

 Используем теорему о движении центра масс:
Используем теорему о движении центра масс: 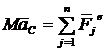 ;
; 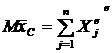 , так как
, так как 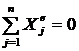 и
и ![]() , то
, то 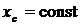 ;
; ![]() (рис. 73),
(рис. 73), 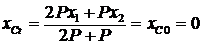 ;
; ![]() (рис. 74).
(рис. 74). 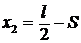 ;
; ![]() ;
; ![]() .
.
Верен ответ 3. Остальные ответы неверны. В ответе 1 не учитывается знак минус координаты ![]() . В ответе 2 неверное заключение. В ответе 4 координата
. В ответе 2 неверное заключение. В ответе 4 координата ![]() неверна,
неверна, 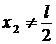 ;
; ![]() .
.
№ 39
Верен ответ 4. Запишем для этой системы дифференциальное уравнение центра масс: 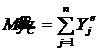 ;
; 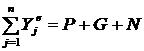 (рис. 75);
(рис. 75); ![]() ;
; 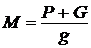 ;
; ![]() ;
; 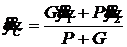 ;
; ![]() ;
; 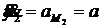
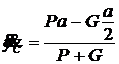 ;
; 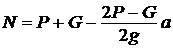 .
.
В ответе 1 найдена статическая реакция. В ответе 2 неверно найдено ускорение ![]() . В ответе 3 не учитывается направление
. В ответе 3 не учитывается направление ![]() .
.
№ 40
Верен ответ 2 (см. рис. 27).
Движение автомобиля можно объяснить, используя теорему о движении центра масс. Действительно, силы давления газа в двигателе являются силами внутренними, они не могут привести в движение систему. Движение происходит за счет сил трения, приложенных к колесам со стороны дороги. Двигатель передает ведущему колесу вращающий момент (рис.76). При этом точка касания В стремится скользить влево, а к колесу будет приложена сила трения, направленная вправо. Эта внешняя сила и позволяет двигаться автомобилю вправо (см. рис. 76).
 |

 К ведомому колесу (рис. 77), не связанному с двигателем, приложена сила давления на ось Р, параллельная пути. Под ее действием все колесо, а с ним и точка касания А колеса о грунт стремится сдвинуться вперед, а сила трения будет направлена назад. Она тормозит движение и является тоже внешней.
К ведомому колесу (рис. 77), не связанному с двигателем, приложена сила давления на ось Р, параллельная пути. Под ее действием все колесо, а с ним и точка касания А колеса о грунт стремится сдвинуться вперед, а сила трения будет направлена назад. Она тормозит движение и является тоже внешней.
В ответе 1 (см. рис. 26) неверно обозначены колеса.
Если вращающий момент ![]() , оба колеса становятся ведомыми (рис. 78). Движение автомобиля по гладкой плоскости (без внешних сил) невозможно.
, оба колеса становятся ведомыми (рис. 78). Движение автомобиля по гладкой плоскости (без внешних сил) невозможно.
№ 41
Если провести через центр тяжести танцора ось Oz то внешние силы (вес человека и нормальная реакция плоскости) будут параллельны оси (если пренебречь силами трения). Тогда по теореме о кинетическом моменте 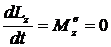 ;
; ![]() ;
; 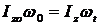 ; где
; где ![]() .
.
Если танцор увеличит момент инерции, например разведением рук в стороны, то скорость вращения уменьшится и наоборот. Следовательно, изменяя момент инерции, танцор может изменять в танце свою угловую скорость. Верен ответ 1.
№ 42
Рассмотрим движение системы, состоящей из вращающегося стержня и двух точек. Внешние силы веса ![]() и реакции опор С и D относительно оси z моментов не создают. Следовательно,
и реакции опор С и D относительно оси z моментов не создают. Следовательно, 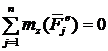 и
и 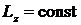 ; найдем
; найдем ![]() и
и
![]() . (рис. 79).
. (рис. 79). 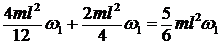 (рис. 80). Но
(рис. 80). Но ![]() , тогда
, тогда 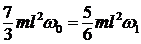 ; тогда
; тогда ![]() .
.
Верен ответ 4.
Ответ 3 неверен. Перепутано условие задачи и взято за начальное положение точки А1 и В1, за конечное — А, В.
В ответе 2 ![]() , это неверно, так как
, это неверно, так как 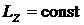 ;
; ![]() , то и
, то и 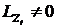 ; и
; и ![]() .
.
Ответ 1 будет верен, если точки А и В не будут перемещаться, а они переместились.
№ 43
Неверен ответ 3. Так как все векторы количеств движения лежат в одной плоскости, то кинетический момент этой системы ![]() относительно оси z и относительно центра О одинаков:
относительно оси z и относительно центра О одинаков:
![]() ,
,
где ![]() ;
;
![]() — кратчайшее расстояние от оси Oz или центра О до
— кратчайшее расстояние от оси Oz или центра О до ![]() ;
;
![]() не является кратчайшим расстоянием от центра О до
не является кратчайшим расстоянием от центра О до ![]() ;
;
![]() не является моментом количества движения
не является моментом количества движения ![]() .
.
№ 44
Теорема об изменении кинетического момента системы в скалярной форме пишется так: ![]() , если
, если 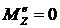 , то
, то ![]() .
.
Верен ответ 3. Ответы 1 и 2 перепутаны. Ответ 4 неверен, так как ![]() , если
, если ![]() , то
, то 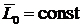 .
.
 № 45
№ 45
![]() (рис. 81).
(рис. 81).
1. ![]() — верно.
— верно.
2. ![]() ;
; 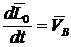 — верно.
— верно.
3. ![]() — верно.
— верно.
4. ![]() . Ответ 4 неверен.
. Ответ 4 неверен.
№ 46
Верен ответ 3.
Для решения задачи применим теорему об изменении кинетического момента системы:![]() (силы P, Q параллельны Oz, реакции опор пересекают Oz (рис. 82)).
(силы P, Q параллельны Oz, реакции опор пересекают Oz (рис. 82)).
![]() ;
; 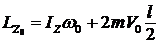 ; где
; где ![]() ;
; 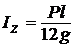 ;
;
тогда 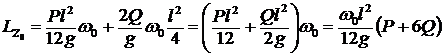 ; найдем
; найдем 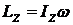 ; но
; но ![]() . Тогда
. Тогда 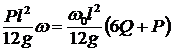 ; получим
; получим ![]() .
.
Ответ 1 неверен, так как ![]() .
.
Ответ 2. ![]() ;
; 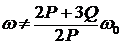 .
.
№ 47
Верен ответ 1.
 На данную систему действуют силы тяжести и реакции опор. Все они пересекают ось z (рис. 83), следовательно,
На данную систему действуют силы тяжести и реакции опор. Все они пересекают ось z (рис. 83), следовательно, ![]() ;
; 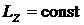 ;
; ![]() .
.
![]() ;
; 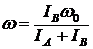 .
.
В ответе 2 ![]() ,
, 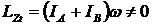 .
.
В ответе 3 ошибка в счете. ![]() ;
; 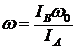 .
.
№ 48
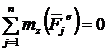 (рис. 84).
(рис. 84). 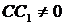 ;
; ![]() ;
; 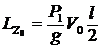 ;
; 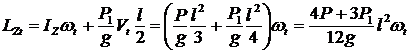 ;
;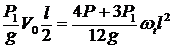 , так как
, так как ![]() . Получим
. Получим 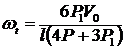 .
.
Верен ответ 2.
Ответ 1 неверен, так как ![]() ;
; 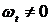 .
.
Ответ 3. ![]() ;
; 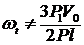 . Потерян момент количества движения пули.
. Потерян момент количества движения пули.
В ответе 4 неверно вычислен момент инерции доски: 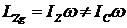 ;
; ![]() ;
; 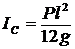 ;
; 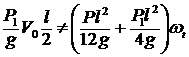 ;
; 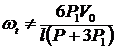 .
.
№ 49
Момент количества движения точки относительно центра О 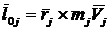 — векторная величина. Кинетический момент системы
— векторная величина. Кинетический момент системы 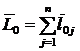 (рис. 85) будет тоже вектором
(рис. 85) будет тоже вектором 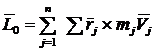 , т. е. равенства (2) и (3) верны, неверен ответ 1.
, т. е. равенства (2) и (3) верны, неверен ответ 1.
№ 50
Верен ответ 2. Применим теорему об изменении кинетического момента системы (рис. 86): ![]() ;
; 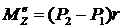 ;
; ![]() ;
; 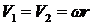 .
.
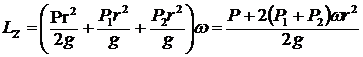 , где
, где 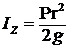 .
. 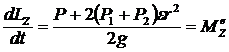 .
. 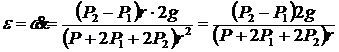 .
.
Ответ 1 неверный, так как ![]() , то
, то 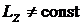 и
и ![]() ,
, ![]() .
.
В ответах 3, 4 ошибки в вычислениях ![]() .
.
№ 51
Неверен ответ 1. Шатун АВ совершает плоскопараллельное движение (рис. 87), энергию нельзя считать по формуле 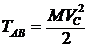 , как для поступательно движущегося тела. В данный момент
, как для поступательно движущегося тела. В данный момент ![]() ;
; ![]() . Скорость всех точек звена АВ определяются как вращательные вокруг м. ц. с. точки В и энергию АВ можно считать как энергию тела, вращающегося вокруг точки В
. Скорость всех точек звена АВ определяются как вращательные вокруг м. ц. с. точки В и энергию АВ можно считать как энергию тела, вращающегося вокруг точки В
![]() ;
; 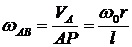 ;
; ![]()
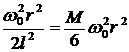 .
.
Ответ 2 верен. Энергию АВ можно считать и по общей формуле ![]() , как энергию тела, совершающего плоскопараллельное движение:
, как энергию тела, совершающего плоскопараллельное движение: 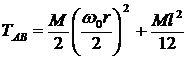
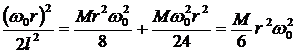 .
.
Ответ 3 верен.
№ 52
Кулиса О1В совершает вращательное движение (рис. 88). Ее энергия ![]() .
.
Верен ответ 4. Чтобы найти ωК, рассмотрим движение точки А. Ее движение сложное.
![]() ;
; 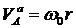 ;
; ![]() ;
; 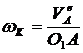 ;
; ![]() ;
;
![]() ;
; 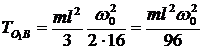 .
.
Ответы 2 и 3 неверны. Записана энергия тела в поступательном (2) и плоскопараллельном движении, а кулиса совершает вращательное движение и ее энергия вычисляется по формуле 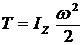 .
.
Здесь ![]() — момент инерции относительно оси вращения. В данном случае
— момент инерции относительно оси вращения. В данном случае ![]() ;
; 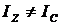 , поэтому ответ 1 нельзя считать верным.
, поэтому ответ 1 нельзя считать верным.
№ 53
Неверен ответ 3. Такой была бы энергия диска, если бы его тащили волоком по плоскости, т. е. перемещали поступательно. На самом деле, кроме поступательного движения у диска есть еще и вращение, и его энергия ищется как сумма двух энергий: в поступательном движении со скоростью ![]() и вращательном вокруг оси С .
и вращательном вокруг оси С .
Ответ 2 верен. Верен и ответ 1. Скорости всех точек диска определяются как вращательные вокруг м. ц. с. Р, а потому Т можно считать как энергию вращения вокруг Р, т. е. 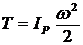 .
.
№ 54
Верными являются ответы 1 и 3. В общем случае шатун АВ совершает плоскопараллельное движение и его энергию следует считать по формуле, записанной в ответе 1. Но в данный момент времени ![]() ,
, 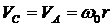 . Имеем случай мгновенно-поступательного движения и энергию АВ можно считать как энергию в поступательном движении:
. Имеем случай мгновенно-поступательного движения и энергию АВ можно считать как энергию в поступательном движении:
![]() (ответ 3).
(ответ 3).
Неверен ответ 2. ![]() , вращение в этот момент у шатуна отсутствует, нет и энергии вращения. Поэтому ответ 2 неверен. Кроме того, есть еще одна ошибка, вместо
, вращение в этот момент у шатуна отсутствует, нет и энергии вращения. Поэтому ответ 2 неверен. Кроме того, есть еще одна ошибка, вместо ![]() поставлена
поставлена ![]() .
.
№ 55
Верен ответ 3. Цилиндр движется поступательно вместе с колодкой вдоль плоскости, и его энергия ![]() .
.
Итак, если катиться по плоскости цилиндр не может, то ![]() и его скорость во вращательном движении и энергия равны 0. Поэтому ответы 1 и 2 неверны.
и его скорость во вращательном движении и энергия равны 0. Поэтому ответы 1 и 2 неверны.
№ 56
Рассмотрим движение системы, состоящей из невесомого стержня и двух точек А и В (рис. 89). Энергия этой системы
![]() .
.
Для решения задачи применим теорему об изменении кинетической энергии 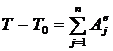 .
. ![]() , так как система в момент
, так как система в момент ![]() неподвижна.
неподвижна.
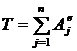 ;
; 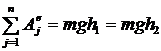 ;
; ![]() ;
; 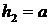 ;
; 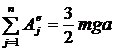 ; приравняв Т и
; приравняв Т и 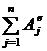 :
: ![]() , получим
, получим 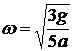 .
.
Верен ответ 1. Остальные неверны. В ответе 2 неверно считается 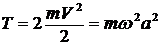 , потому что
, потому что ![]() и нельзя писать в формуле просто V ,нужно указать, скорость какой точки берется. В ответе 3 неверно вычисляется работа:
и нельзя писать в формуле просто V ,нужно указать, скорость какой точки берется. В ответе 3 неверно вычисляется работа:
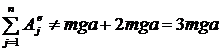 ; вместо
; вместо 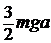 ;
; 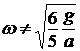 .
.
В ответе 4 неверно находится ![]() и
и 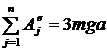 ;
; 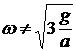 .
.
№ 57
Кинетическая энергия системы равна сумме кинетических энергий двух данных точек. Энергия одной точки ![]() , тогда системы
, тогда системы ![]() .
.
Верен ответ 3. Ответ 1 неверен, вместо энергии системы записана энергия одной только точки. Неверен и ответ 2: ![]() . Поскольку есть верный ответ среди данных ответов, заключение 4 неверно.
. Поскольку есть верный ответ среди данных ответов, заключение 4 неверно.
№ 58
В первом случае диск вращается вокруг неподвижной оси (рис. 90 а). Его энергия ![]() ;
; 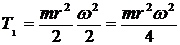 , где
, где ![]() .
.
Во втором случае его движение будет плоскопараллельным (рис.90 б). Его энергия
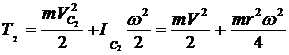 ;
; 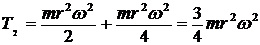 ;
;
![]() .
.
Сравнивая, видим, во втором случае энергия в 3 раза больше. Верен ответ 2. Ответ 1 неверен. ![]() нельзя считать как энергию тела в поступательном движении:
нельзя считать как энергию тела в поступательном движении:
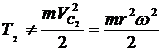 , поэтому
, поэтому 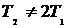 .
.
Ответ 3 тоже неверен. Совершенно неверно считать энергию ![]() только как энергию вращения, т. е.
только как энергию вращения, т. е. 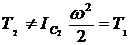 .
.
Ответ 4 неверен. Верный ответ 2.
№ 59
Верен ответ 4. Шайба вращается вокруг оси О с угловой скоростью w. Ее энергия ![]() ;
; 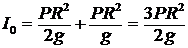 ;
; ![]() .
.
Остальные ответы неверны. В ответе 1 записана энергия тела при поступательном движении, а нужно при вращательном. В ответе 2 записана формула для вычисления энергии тела, вращающегося вокруг центра тяжести, а данное тело вращается вокруг точки, лежащей на ободе, и его энергия не 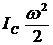 , а
, а ![]() , как в 3-м и 4-м случаях. Но в ответе 3 исходная формула взята верно, а момент инерции — нет. Нужно
, как в 3-м и 4-м случаях. Но в ответе 3 исходная формула взята верно, а момент инерции — нет. Нужно ![]() посчитать по теореме о моментах инерции относительно параллельных осей:
посчитать по теореме о моментах инерции относительно параллельных осей:![]() ,
,
т. е. ![]() .
.
№ 60
Верен ответ 4. Действительно, когда цилиндр скользит по плоскости, его энергия ![]() , как энергия тела в поступательном движении. Если же цилиндр будем катить по плоскости, то энергия его
, как энергия тела в поступательном движении. Если же цилиндр будем катить по плоскости, то энергия его 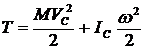 , т. е. как энергия тела в плоскопараллельном движении. Подставив значение
, т. е. как энергия тела в плоскопараллельном движении. Подставив значение ![]() , имеем
, имеем
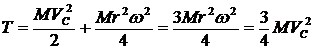 , так как
, так как ![]() . Сравним энергию цилиндра в том и другом случае. Во втором случае она больше на
. Сравним энергию цилиндра в том и другом случае. Во втором случае она больше на ![]() . Остальные ответы неверны.
. Остальные ответы неверны.
В ответе 1 энергия изменится, так как изменится вид движения. Цилиндр, кроме поступательного движения будет еще участвовать во вращательном движении и добавится энергия этого вращения. В ответе 2 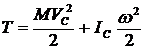 . Формула применяется верно, но
. Формула применяется верно, но ![]() считается равным
считается равным ![]() , как для полого цилиндра, а у нас сплошной цилиндр, для него
, как для полого цилиндра, а у нас сплошной цилиндр, для него ![]() , следовательно,
, следовательно, 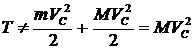 .
.
В ответе 3 ![]() , потому что вычислена энергия только во вращательном движении вокруг С, но не подсчитана энергия в поступательном движении вместе с центром масс.
, потому что вычислена энергия только во вращательном движении вокруг С, но не подсчитана энергия в поступательном движении вместе с центром масс.
№ 61
Верен ответ 4. ![]() ;
; 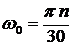 ;
; ![]() ;
; 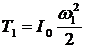 ;
; ![]() ;
; 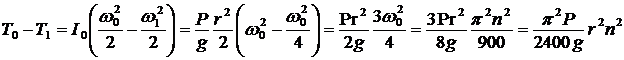 .
.
Ответ 3 неверный. Нужно было перевести  в
в ![]() по формуле
по формуле 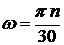 ;
; 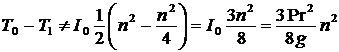 .
.
Ответ 2 неверный. ![]() ,
, ![]() следует перевести в радианы на секунду.
следует перевести в радианы на секунду.
Ответ 1 неверный. Неверно считается 
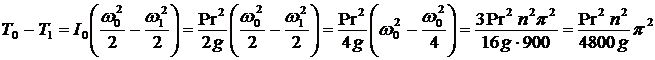 .
.
№ 62
Для решения задачи применим теорему о кинетической энергии системы, рассматривая колесо (рис. 91) как систему точек: 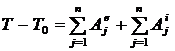 , так как система неизменяемая,
, так как система неизменяемая, 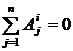 . В начальный момент система неподвижна,
. В начальный момент система неподвижна, ![]() . Вычислим кинетическую энергию колеса:
. Вычислим кинетическую энергию колеса:
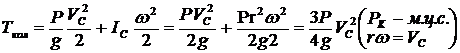 .
.
Работа внешних сил: 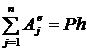 ;
;  ;
; ![]() . Тогда
. Тогда 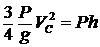 ;
; ![]() .
.
Верен ответ 1. В ответах 2 и 3 неверно считается кинетическая энергия колеса. ![]() ;
; 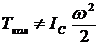 , так как движение колеса не является ни поступательным, ни вращательным. Колесо совершает плоскопараллельное движение. Его энергия
, так как движение колеса не является ни поступательным, ни вращательным. Колесо совершает плоскопараллельное движение. Его энергия ![]() .
.
№ 63
Запишем теорему о кинетической энергии системы (стержень на рис. 92 — система точек) 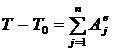 . (
. (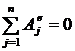 — система неизменяемая).
— система неизменяемая).
![]() ;
; 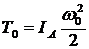 ;
; 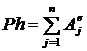 ;
; 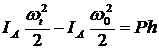 ;
; ![]() ;
; 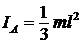 ;
; 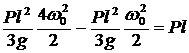 ;
; ![]() ;
; ![]() ;
; 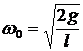 .
.
Стержень совершает вращательное движение и его энергия 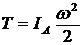 .
.
Верен ответ 2.
В ответе 1 неверно считается кинетическая энергия стержня 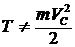 , потому что движение стержня не является поступательным. Заключение в ответе 3 неверно, так как есть верный ответ (2) среди двух приведенных ответов.
, потому что движение стержня не является поступательным. Заключение в ответе 3 неверно, так как есть верный ответ (2) среди двух приведенных ответов.
№ 64
Стержень (рис. 93) совершает плоскопараллельное движение и его энергия ![]() , (где С — центр масс стержня). Зная скорость точки А (
, (где С — центр масс стержня). Зная скорость точки А (![]() ), найдем скорость точки С и угловую скорость стержня. Для этого найдем м. ц. с. стержня АВ. Он находится в точке
), найдем скорость точки С и угловую скорость стержня. Для этого найдем м. ц. с. стержня АВ. Он находится в точке ![]() , с помощью этого центра найдем
, с помощью этого центра найдем ![]() и
и ![]() :
:
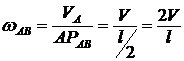 ;
; 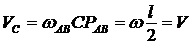 .
.
Подставим значения ![]() и
и ![]() , имеем
, имеем 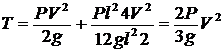 , где
, где 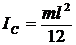
Верен ответ 3. В ответах 1 и 2 энергия стержня считается как энергия тела в поступательном (1) или вращательном (2) движениях. Но движение стержня плоскопараллельное, и энергия его равна сумме энергий в поступательном и вращательном движениях стержня, т. е. ![]() .
.
В ответе 4 кинетическая энергия стержня считается верно, как сумма энергий, но неверно считается
![]() ;
; 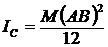 .
.
ЛИТЕРАТУРА
1. Тарг курс теоретической механики: Учебник для втузов. — М.: Высшая школа, 2001.
2. Яблонский теоретической механики. — М.: Высшая школа, 1977.
3. Сборник задач по теоретической механике: Учебное пособие для вузов / , , . — М.: Высшая школа, 1974.
4. Мещерский задач по теоретической механике: Учебное пособие для вузов. — М.: Наука, 1981.
ОГЛАВЛЕНИЕ
Введение …………………………………………………………………..……… 3
Раздел 1. Введение в динамику системы ………………………………………. 3
Тема 1. Понятие механической системы ……………………………………….. 4
Тема 2. Теорема о моментах инерции относительно параллельных осей … 11
Раздел II. Основные теоремы динамики системы точек ……………………... 17
Тема 3. Теоремы об изменении количества движения и о движении
центра масс ………………………………………………………………………. 18
Тема 4. Теоремы об изменении кинетического момента …………………….. 29
Тема 5. Теорема об изменении кинетической энергии системы …………….. 37
Ответы и решения к контрольным вопросам и заданиям …………………… 45
Литература ……………………………………………………………………… 67

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 |




