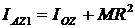 ;
; ![]() ;
; ![]() ;
;
| (7) |
Контрольные вопросы и задания к теме 2
№ 11
Вычислить момент инерции круглого диска относительно диаметра диска.
1. 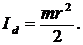
2. 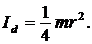
3. 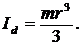
4. 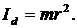
№12
Вычислить момент инерции однородного круглого диска веса Р и радиуса r относительно оси l1, лежащей в его плоскости и отстоящей от центра тяжести С диска на расстояние а = ![]() .
.
1. 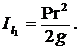
2. 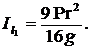
3. 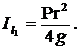
4. 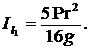
№ 13
Вычислить радиус инерции однородного круглого диска весом Р и радиусом ![]() относительно оси l1, лежащей в его плоскости и отстоящей от центра тяжести С диска на
относительно оси l1, лежащей в его плоскости и отстоящей от центра тяжести С диска на 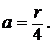
1. 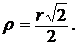
2. 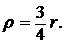
3. 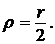
4. 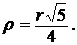
№ 14
Определить радиус инерции сплошного круглого цилиндра относительно его оси.
1. ![]() .
.
2. 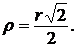
3. 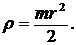
Здесь r — радиус цилиндра.
№ 15
Вычислить момент инерции диска относительно его касательной.
1. 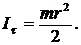
2. 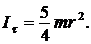
3. 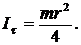
4. 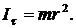
№ 16
Определить радиус инерции однородного тонкого стержня длиной l относительно оси, перпендикулярной к стержню в конце его.
1. 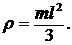
2. ![]()
3. 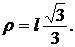
 № 17
№ 17
Определить момент инерции однородной пластинки массой М относительно оси z1 (рис. 10).
1. 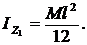
2. 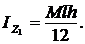
3. 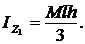
4. 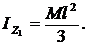
№ 18
Найти момент инерции стержня массой М и длиной 2а относительно оси z проходящей через его середину и образующей угол ![]() с направлением стержня.
с направлением стержня.
1. 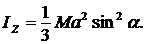
2. 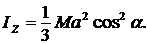
3. 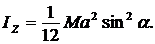
4. 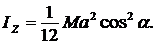
№ 19
Определить радиус инерции ![]() прямоугольника, основание которого 0,2 м, а высота 0,4 м, относительно оси y, проходящей через центр тяжести параллельно основанию.
прямоугольника, основание которого 0,2 м, а высота 0,4 м, относительно оси y, проходящей через центр тяжести параллельно основанию.
1. ![]() = 0,116 м.
= 0,116 м.
2. ![]() = 0,232 м.
= 0,232 м.
3. ![]() = 0,303 м.
= 0,303 м.
№ 20
Определить момент инерции круга массой М и радиусом а относительно хорды АВ, отстоящей от центра на половину радиуса.
1. 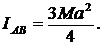
2. 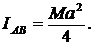
3. 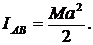
Раздел II. ОСНОВНЫЕ ТЕОРЕМЫ ДИНАМИКИ СИСТЕМЫ ТОЧЕК
Раздел состоит из трех тем. В результате изучения раздела студент должен:
знать а) определение количества движения, кинетического момента и кинетической энергии системы; б) формулировки основных теорем динамики системы в дифференциальной и интегральной формах; в) законы сохранения количества движения, координаты центра масс и кинетического момента системы;
уметь а) практически вычислять количество движения, кинетический момент, кинетическую энергию системы; б) вычислять работу, моменты, импульсы внешних сил, приложенных к системе; в) практически применять при решении задач основные теоремы динамики системы и закон сохранения количества движения, координаты центра масс, кинетического момента системы;
помнить а) формулы для вычисления количества движения, кинетического момента и кинетической энергии системы работы сил; б) формулы, выражающие основные теоремы динамики системы; в) порядок решения задач.
Тема 3. ТЕОРЕМЫ ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ
И О ДВИЖЕНИИ ЦЕНТРА МАСС
Основные теоремы динамики являются следствиями, вытекающими из основного закона динамики. Рассмотрим эти теоремы для системы точек.
Пусть имеем механическую систему, состоящую из n точек. Запишем для произвольной точки Аj теорему об изменении количества движения точки в дифференциальной форме:
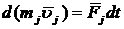 или
или ![]() ,
,
где ![]() ;
; ![]() — внешняя сила;
— внешняя сила; ![]() — внутренняя сила.
— внутренняя сила.
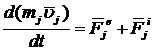 , написав подобные равенства для каждой из n точек системы, сложим их. Получаем:
, написав подобные равенства для каждой из n точек системы, сложим их. Получаем:
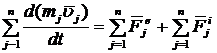 .
.
Внесем знак ![]() под знак производной:
под знак производной:
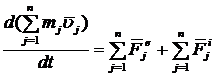 .
.
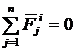 — по свойству внутренних сил;
— по свойству внутренних сил;
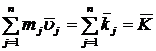 — вектор количества движения системы точек.
— вектор количества движения системы точек.
Количеством движения системы называются вектор ![]() , равный геометрической сумме векторов количеств движения всех точек системы. Заменив
, равный геометрической сумме векторов количеств движения всех точек системы. Заменив
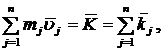
имеем
| (1) |
Равенство (1) выражает теорему об изменении количества движения системы в дифференциальной векторной форме: производная от количества движения системы по времени равна сумме всех внешних сил, действующих на систему.
Проинтегрировав равенство (1), получим:
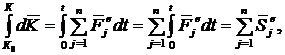
| (2) |
Равенство (2) выражает теорему в интегральной векторной форме: изменение количества движения системы за некоторый промежуток времени равно сумме импульсов всех внешних сил, действующих на систему за тот же промежуток времени.
Из выражений (1) и (2) следует, что количество движения системы зависит только от внешних сил, внутренние силы изменить количество движения системы не могут. Обозначим проекции векторов ![]() а
а 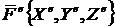 . Спроектировав на декартовы оси равенства (1) и (2), получим:
. Спроектировав на декартовы оси равенства (1) и (2), получим:
| (3) |
| (4) |
Имеем скалярное дифференциальное выражение теоремы об изменении количества движения системы (3): производная от проекции количества движения системы на какую-либо ось по времени равна сумме проекций всех внешних сил на ту же ось. Скалярное интегральное выражение этой же теоремы (4): изменение проекции количества движения системы на какую-либо ось по времени равно сумме проекций импульсов всех внешних сил на туже ось.
Частные случаи рассматриваемой теоремы
1) 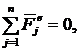 тогда
тогда 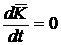 .
.
| (5) |
— закон сохранения количества движения системы.
2) 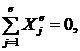 тогда
тогда 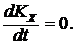
| (6) |
— закон сохранения проекции количества движения.
Пример. Из орудия весом Р2 вылетает снаряд в горизонтальном направлении весом Р1 со скоростью ![]() . Найти скорость после вылета (скорость отката)
. Найти скорость после вылета (скорость отката) ![]() (рис. 11).
(рис. 11).
 |
Если рассмотреть орудие и снаряд как одну систему, то давление пороховых газов
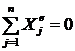 и
и 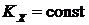 . Наблюдается сохранение проекции количества движения системы на ось х. В начальный момент система неподвижна:
. Наблюдается сохранение проекции количества движения системы на ось х. В начальный момент система неподвижна: 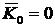 и
и 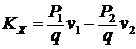 , но
, но 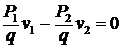 .
.
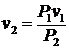 — скорость отката орудия.
— скорость отката орудия.
Примечание. Практическое значение теоремы в том, что при соответствующем выборе механической системы исключаются из рассмотрения все неизвестные внутренние силы. Теорема применяется в теории удара, динамики точки переменной массы, динамике сложных сред (газ, жидкость).
Выражение количества движения системы через скорость центра масс
Если число точек системы велико, то определить вектор ![]() по формуле
по формуле 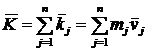 трудно, а иногда невозможно. В этом случае количество движения системы вычисляется через скорость центра масс.
трудно, а иногда невозможно. В этом случае количество движения системы вычисляется через скорость центра масс.
Что такое центр масс системы, уже знаем. Положение этой точки определяется координатами:
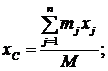
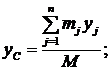
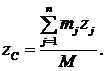
Умножим обе части этих равенств на массу системы М, получим:
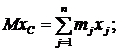
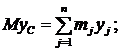
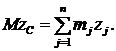
Продифференцируем обе части этих равенств по времени:
| (7) |
Но xC, yC, zC — координаты точки C — центра масс, а ![]() — проекции скорости точки С на оси координат, т. е.
— проекции скорости точки С на оси координат, т. е. ![]() . Координаты точки
. Координаты точки ![]() системы —
системы — ![]() а
а 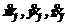 — проекции скорости
— проекции скорости 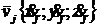 . Соответственно система (7) определяет проекции векторов количеств движения точки С
. Соответственно система (7) определяет проекции векторов количеств движения точки С ![]() в левой части и вектора
в левой части и вектора 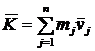 в правой части. Но если равны проекции векторов, то равны и сами векторы:
в правой части. Но если равны проекции векторов, то равны и сами векторы: 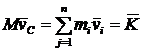 ;
;
| (8) |
 Вывод. Количество движения системы равно произведению массы всей системы на скорость центра масс.
Вывод. Количество движения системы равно произведению массы всей системы на скорость центра масс.
С помощью последней формулы очень легко можно вычислить количество движения системы, скорость центра масс которой известна.
Пример. Вычислить количество движения колеса весом Р, центр масс которого имеет скорость ![]() (рис. 12). Величину
(рис. 12). Величину 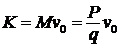 определили по формуле (8). Направлен
определили по формуле (8). Направлен ![]() так же, как и
так же, как и ![]() .
.
Теорема о движении центра масс
Центр движется как материальная точка, масса которой равна массе всей системы, и к которой приложены все внешние силы, действующие на систему.
Доказательство. Возьмем систему, состоящую и n материальных точек. Пусть точка ![]() , скорость которой
, скорость которой ![]() , ускорение
, ускорение ![]() является центром масс данной системы. Выразим количество движения этой системы через скорость центра масс:
является центром масс данной системы. Выразим количество движения этой системы через скорость центра масс: ![]() . Обе части этого равенства продифференцируем по времени:
. Обе части этого равенства продифференцируем по времени:![]() , но
, но 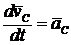 (из кинематики точки); а
(из кинематики точки); а 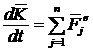 (из теоремы об изменении количества движения системы).
(из теоремы об изменении количества движения системы).
Тогда | (9) |
что и требовалось доказать. Спроектируем это равенство на оси Oxyz, обозначив проекции ![]() —
— 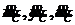 , а
, а![]() —
— 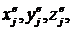 где
где ![]() — центр масс.
— центр масс.
| (10) |
Называются эти уравнения дифференциальными уравнениями движения центра масс. С их помощью можно решать первую и вторую задачи динамики системы. Из выражений (9) и (10) видно, что внутренние силы на движение центра масс не влияют.
Частные случаи
1. Если 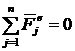 , то
, то ![]() ;
; 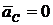 .
. ![]() — центр масс такой системы движется равномерно и прямолинейно.
— центр масс такой системы движется равномерно и прямолинейно.
Если 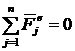 и
и ![]() , то
, то 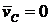 .
.
Отсюда видим, что центр масс остается неподвижным. Этот результат выражает закон сохранения положения центра масс системы.
2. Если 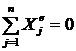 , то
, то ![]() ;
; 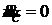 ;
; ![]() .
.
Если же в начальный момент центр масс неподвижен, то ![]() , тогда
, тогда 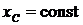 — закон сохранения координаты центра масс.
— закон сохранения координаты центра масс.
Пример. Рассмотрим движение человека по абсолютно гладкой горизонтальной плоскости. На человека действуют внешние силы: Р – вес его и реакция плоскости N (нормальная). Если ось х взять вдоль плоскости, то 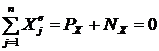 ;
; ![]() ;
; 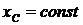 . Центр масс человека остается неподвижным, т. е. вдоль абсолютно гладкой плоскости человек перемещаться не может (его мускульные усилия будут внутренними силами, а внутренние силы на движения центра масс не влияют).
. Центр масс человека остается неподвижным, т. е. вдоль абсолютно гладкой плоскости человек перемещаться не может (его мускульные усилия будут внутренними силами, а внутренние силы на движения центра масс не влияют).
Если же плоскость негладкая, то 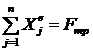 ,
, 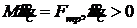 , центр масс перемещается ускоренно по горизонтали. Сила трения при этом направлена в сторону движения человека. Она позволяет ему двигаться.
, центр масс перемещается ускоренно по горизонтали. Сила трения при этом направлена в сторону движения человека. Она позволяет ему двигаться.
Порядок решения задач с помощью закона сохранения количества движения системы
1. Изобразить на рисунке все внешние силы.
2. Выбрать систему координат.
3. Записать теорему об изменения главного вектора количеств движения системы материальных точек в проекциях на оси координат.
4. Если сумма проекций импульсов внешних сил на ось окажется равной нулю, например 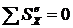 , то следует приравнять между собой проекции на эту ось главного вектора количеств движения системы в начальный и конечный момент времени, т. е.
, то следует приравнять между собой проекции на эту ось главного вектора количеств движения системы в начальный и конечный момент времени, т. е. ![]() , из полученного уравнения определить искомую величину.
, из полученного уравнения определить искомую величину.
Порядок решения задач с помощью теоремы о движении центра масс
1. Изобразить на рисунке все внешние силы системы.
2. Выбрать систему осей координат.
3. Записать дифференциальные уравнения движения центра масс:
| (11) |
4. Вычислить суммы проекций всех внешних сил системы на оси декартовых координат и подставить их в уравнения (11).
5. В зависимости от условия решать прямую либо обратную задачи динамики.
Контрольные вопросы и задания к теме 3
№ 21
Бревно весом Р перекатывается на двух катках весом Q каждый (рис. 13). Определить количество движения системы, если бревно движется со скоростью v.
1. 
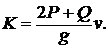
2. 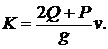
3. 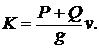
№ 22
 Два шара весом A — 5H и B — 3H соединены с вертикальной осью ЕД горизонтальным стержнем АВ длиной 20 см и весом 10Н, прикрепленным к оси в точке О, отстоящей на 5 см от шара А.
Два шара весом A — 5H и B — 3H соединены с вертикальной осью ЕД горизонтальным стержнем АВ длиной 20 см и весом 10Н, прикрепленным к оси в точке О, отстоящей на 5 см от шара А.
Вся система вращается вокруг оси ЕД, делая 10 оборотов в минуту. Определить количество движения системы (рис. 14).
1. К = 7 кгм/с.
2. К = 0,07 кгм/с.
3. К = 1,2 кгм/с.
№ 23
 Однородная квадратная рама АВСД со стороной а вращается вокруг оси АВ с постоянной угловой скоростью
Однородная квадратная рама АВСД со стороной а вращается вокруг оси АВ с постоянной угловой скоростью ![]() . Вокруг оси СВ, совпадающей с диагональю рамы, вращается однородный диск весом Р1 (рис. 15).
. Вокруг оси СВ, совпадающей с диагональю рамы, вращается однородный диск весом Р1 (рис. 15).
Определить количество движения системы, если вес рамы Р2.
1. К = 0.
2. 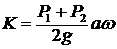 .
.
3. 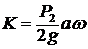
4. 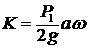 .
.
№ 24
Матрос весом Р перемещается по шлюпке весом ![]() с относительной скоростью u. В начальный момент шлюпка имела скорость
с относительной скоростью u. В начальный момент шлюпка имела скорость ![]() . Определить, через сколько времени ее скорость станет равной нулю, если сопротивление воды постоянно и равно R (человек движется в сторону движения лодки).
. Определить, через сколько времени ее скорость станет равной нулю, если сопротивление воды постоянно и равно R (человек движется в сторону движения лодки).
1. 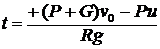 .
.
2. 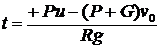 .
.
№ 25
На лодке, движущейся со скоростью v0, находится человек. С какой скоростью будет перемещаться лодка, если человек начнет двигаться по ней с относительной скоростью u. Вес лодки ![]() , человека — Р (человек движется в сторону движения лодки). Сопротивлением воды пренебречь.
, человека — Р (человек движется в сторону движения лодки). Сопротивлением воды пренебречь.
1. ![]() .
.
2. 
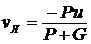 .
.
3. ![]() .
.
№ 26
Кривошип ОА вращается равномерно с угловой скоростью ![]() и приводит в движение колесо II радиусом R и весом Р (рис. 16). Определить количество движения системы, если R1 = R2 = R, ОА — однородный стержень весом Р1.
и приводит в движение колесо II радиусом R и весом Р (рис. 16). Определить количество движения системы, если R1 = R2 = R, ОА — однородный стержень весом Р1.
1. ![]() .
.
2. ![]() .
.
3. ![]() .
.
№ 27

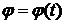 и верхние стержни поворачиваясь, поднимают шары А и В (рис. 17). Весом муфты пренебречь и весом стержней. Шары считать точечными массами весом Р каждый.
и верхние стержни поворачиваясь, поднимают шары А и В (рис. 17). Весом муфты пренебречь и весом стержней. Шары считать точечными массами весом Р каждый.
1. ![]() .
.
2. ![]() .
.
3. ![]() .
.
4. ![]() .
.
 № 28
№ 28
Определить главный вектор количеств движения данной системы, если угловая скорость первого колеса ![]() ,
, ![]() . Вес колес Р1 и Р2, центры тяжести их лежат на осях вращения О1 и О2 (рис. 18).
. Вес колес Р1 и Р2, центры тяжести их лежат на осях вращения О1 и О2 (рис. 18).
1. К = 0.
2. ![]() .
.
3. 
![]() .
.
№ 29
На невесомом стержне, вращающемся вокруг оси О по закону ![]() , находятся на расстоянии ОМ1 = l1, ОМ2 = l2 две точки массой m1 и m2. Определить количество движения этой системы (рис. 19).
, находятся на расстоянии ОМ1 = l1, ОМ2 = l2 две точки массой m1 и m2. Определить количество движения этой системы (рис. 19).
1. ![]() .
.
2. ![]() .
.
3. ![]() .
.
№ 30
Прямоугольный параллелепипед поставлен на горизонтальную плоскость. На него положено тело А весом Р1, а тело В весом Р2 соединено с телом А гибкой нерастяжимой нитью, перекинутой через блок С (рис. 20).
Определить зависимость между скоростью параллелепипеда ![]() и скоростью u тела А по отношению к параллелепипеду, если опорные поверхности гладкие, и в начале движения система покоилась. Вес параллелепипеда Q, весом нити и блока пренебречь.
и скоростью u тела А по отношению к параллелепипеду, если опорные поверхности гладкие, и в начале движения система покоилась. Вес параллелепипеда Q, весом нити и блока пренебречь.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 |




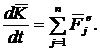
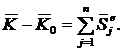
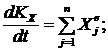
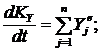
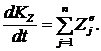
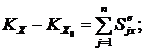
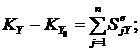
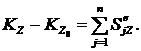
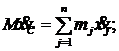
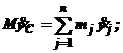
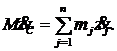
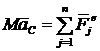 ,
,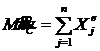 ;
; 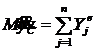 ;
; 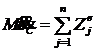 .
.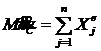 ;
; 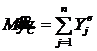 ;
; 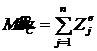 .
.