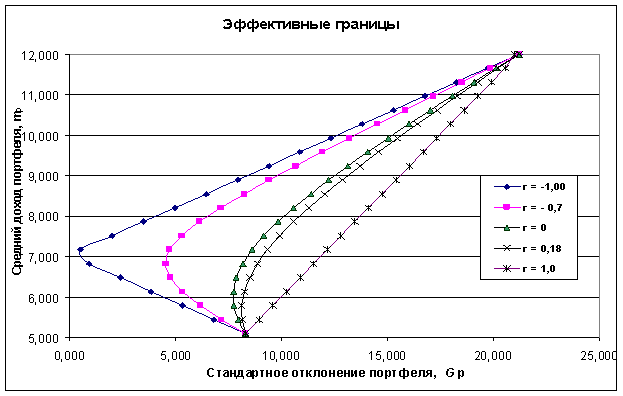
Рис. 4.4. Зависимость средней доходности портфелей от стандартных
отклонений при различных значениях rij
Инвестор всегда выбирает портфель, лежащий на эффективной границе, на основе анализа соотношений риска и доходности.
4.3. Постановка задачи об оптимальном портфеле
В литературе описаны различные подходы к формированию оптимального портфеля с помощью моделей Блэка, Марковица, Тобина.
Задача оптимизации сводится к определению такой структуры состава портфеля инвестиций, чтобы величина ожидаемого дохода и уровень риска соответствовали целям инвесторов. При этом целевой функцией может быть минимизация риска при заданной доходности, либо максимизация дохода при риске не выше заданного. На компоненты вектора Х, представляющего состав портфеля могут накладываться различные ограничения, зависящие от вида сделки, типа участвующих активов, величины открываемых позиций и т. д. Портфели, удовлетворяющие условиям данного рынка, называются допустимыми.
1) В модели Блэка допустимыми являются любые портфели, т. е. вектор Х удовлетворяет лишь основному ограничению:
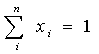. (4.6)
Наличие коротких позиций (отсутствие условия неотрицательности) позволяет реализовать любую, сколь угодно большую доходность, естественно за счет большого риска.
2) Модель Марковица рассматривает в качестве допустимых только стандартные портфели (без коротких позиций). Это значит, что на вектор Х накладываются два ограничения: основное 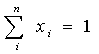и неотрицательности xi ³ 0 для всех i.
Портфель называют стандартным, если инвестор по каждому активу находится в длинной (long) позиции.
Длинная позиция - это обычно покупка актива с намерением его последующей продажи (закрытие позиций). Такая покупка обычно осуществляется при ожидании повышения цены актива в надежде получить доход от разности цен покупки и продажи. Если относительно некоторого актива инвестор уверен в обратном, то есть в понижении его стоимости, то он может совершить сделку, которая называется «короткой продажей» (short sale). Для этого он берет данный актив взаймы у другого инвестора (кредитора), сразу же продает его, а впоследствии покупает на рынке по сниженной цене и возвращает его своему кредитору. При этом он обязан выплатить кредитору текущий доход по активу за время сделки и некоторый процент за предоставление самой возможности сделки (за кредит). На большинстве фондовых бирж короткие продажи вполне допустимы и часто используются, но ввиду их особой рискованности биржи могут вводить ограничения на общую величину коротких позиций в сделках.
В модели Марковица обычно рассматриваются два типа задач оптимизации портфелей: минимального риска при заданном уровне доходности, и максимальной эффективности при уровне риска не превышающем заданного значения.
Портфель Марковица минимального риска. Постановку данной задачи можно интерпретировать следующим образом. Найти вектор X* распределения исходного капитала, минимизирующий риск (вариацию) портфеля
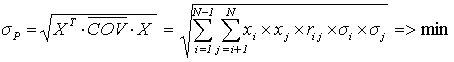(4.7)
при заданной эффективности портфеля
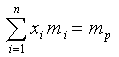, (4.8)
и условии, что сумма долей активов в портфеле должна составлять единицу
S xi = 1,0. (4.9)
Здесь матрица ковариаций i j =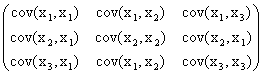 
.
Пример 4.2. Сформировать портфель минимального риска sp из двух видов ценных бумаг А с эффективностью 12% и риском 21,2 и В с эффективностью 5,1% и риском 8,3 при условии, что обеспечивается доходность портфеля (mp =S xi mi) не менее 8,9%. Коэффициент парной корреляции между этими бумагами равен 0,18.
Решение
1. Введем обозначения: x1 - доля в портфеле ценных бумаг А; x2 - доля в портфеле ценных бумаг В,
2. Сформулируем задачу формирования оптимального портфеля по модели Марковица, с учетом исходных данных.
Необходимо найти вектор Х* = (x1, x2), минимизирующий риск портфеля:
sp=
=
=
=
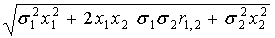® min,
при следующих ограничениях:
- по доходности 12´ x 1 + 5,1´ x 2 ³ 8,9;
- по составу портфеля x 1 + x 2 =1;
- условие неотрицательности x 1, x 2 ³ 0.
Данная задача свелась к задаче квадратического программирования.
3. Решение приведенной задачи можно осуществить графическим методом, либо используя надстройку в Excel Поиск решения.
Графическая иллюстрация решения задачи представлена на рис. 4.5.
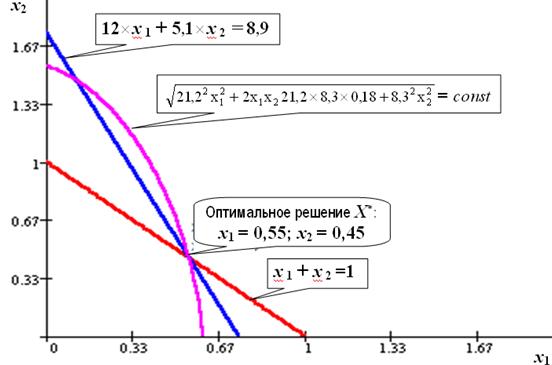
Рис. 4.5. Минимальный риск портфеля равный 12,88 достигается в точке пересечения трех линий (x 1=0,55 и x 2=0,45), соответствующих ограничениям 12´ x 1 + 5,1´ x 2 ³ 8,9 и x1 + x 2 =1 и целевой функции
Для решения с помощью надстройки Поиск решения вначале на листе Excel составляется стандартная форма для решения оптимизационных задач, с использованием надстройки Поиск решения как показано на рис. 4.6. Затем непосредственно используется сама надстройка Поиск решения.
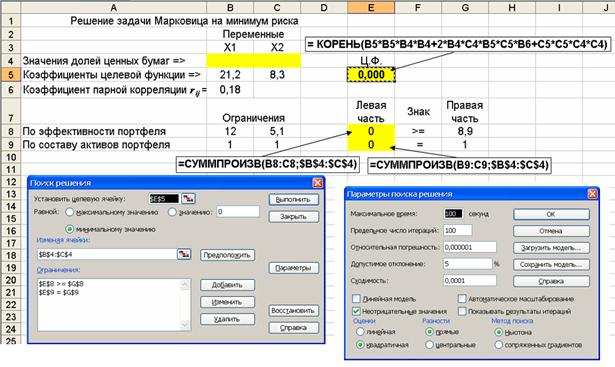
Рис. 4.6. Исходные данные и расчетные формулы
Результаты расчета состава оптимального портфеля по критерию минимального риска представлены на рис. 4.7.
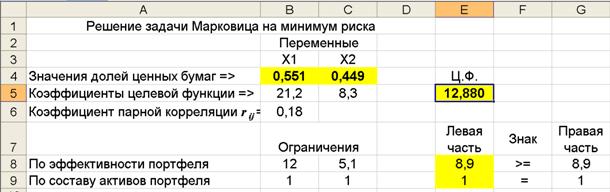
Рис.4.7. Результаты расчета состава оптимального портфеля
В ячейке Е5 получено минимальное значение целевой функции σp = 12,880, а в ячейки B4:C4 записаны значения x1 = 0,551 и x2 = 0,449 - доли ценных бумаг типа A и типа B, соответственно. При этом заданные ограничения удовлетворяются полностью, эффективность портфеля составляет 8,9% (ячейка G8).
Пример 4.3. Сформировать портфель минимального риска из трех ценных бумаг А, В и С (характеристики бумаг приведены в таблице), обеспечиваю-
Показатель
Тип ценной бумаги
A
B
C
Эффективность, mi , %
12
5,1
9,5
Риск, σi
21,2
8,3
14,5
щих среднюю доходность портфеля mp не менее 12,5%. Матрица коэффициентов парной корреляции между ценными бумагами известна:
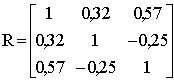
Решение
1. Введем обозначения: x1, x2, x3 – соответствующие доли ценных бумаг А, В и С в составе портфеля.
2. Запишем экономико-математическую модель (ЭММ) задачи формирования оптимального портфеля по модели Марковица в общем виде:
,
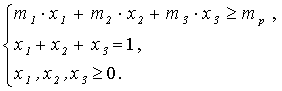
3. Подготовим лист для решения задачи, рис. 4.8. и здесь же предварительно сформируем ковариационную матрицу (ячейки F17:H19), элементы которой рассчитываются по выражению (4.5).
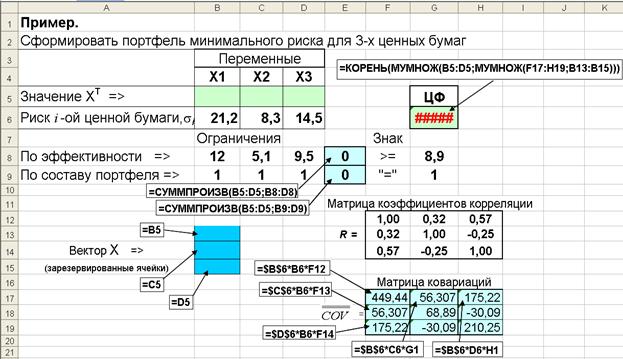
Рис. 4.8. Лист Excel с исходными данными и расчетными формулами для расчета состава оптимального портфеля из трех ценных бумаг
4. Запишем ЭММ задачи в развернутом виде с учетом исходных условий и рассчитанной матрицы ковариаций:
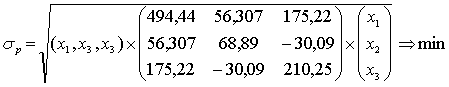
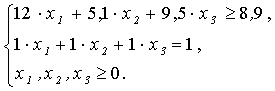
5. В результате решения задачи в ячейках (B5:D5) будут находиться элементы оптимального вектора Х* = (0,23; 0,27; 0,50), минимизирующего риск портфеля, который составляет σp = 1,01 (ячейка G6) и обеспечивающий его эффективность 8,9% (ячейка E8), рис.4.9.
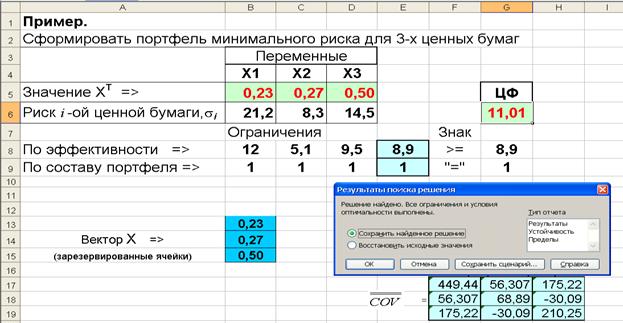
Рис. 4.9. Лист Excel с результатами расчета состава оптимального портфеля из трех ценных бумаг
Портфель Марковица максимальной эффективности. Найти вектор X*, максимизирующий ожидаемую эффективность портфеля
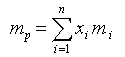=> max (4.10)
при уровне риска не превышающем заданного значения
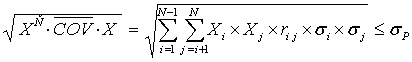, (4.11)
и условии, что сумма долей активов в портфеле должна составлять единицу
S xi = 1,0. (4.12)
Если в оптимальном решении значения xi* ³ 0, то рекомендуется долю xi* наличного капитала вложить в ценные бумаги i-го вида. Если xi* < 0, то следует провести операцию «короткой продажи» и если такая операция невозможна, то необходимо в модель ввести ограничение xi* ³ 0. Вместо операции «короткой продажи» инвестор может воспользоваться денежными средствами по безрисковой ставке.
Особенностью модели Марковица является то, что доходность любого стандартного портфеля не превышает наибольшей доходности активов, из которых он построен.
Пример 4.4. Найти оптимальный портфель максимальной эффективности для трех ценных бумаг R, S и L с известными доходностями mi и риском σi (см. табл.):
R
S
L
mi (%)
12
10,5
11
si
25
10
20
Коэффициенты парной корреляции между ценными бумагами представлены в виде матрицы:
R
S
L
R
1
0,52
0,27
S
0,52
1
0,75
L
0,27
0,75
1
Верхняя граница риска σp не должна превышать 16.
Решение
1. Введем обозначения: x1, x2, x3 – соответствующие доли ценных бумаг типов R, S и L в составе портфеля.
2. Запишем ЭММ задачи формирования оптимального портфеля по модели Марковица в общем виде:
mp= m1´ x1+ m2´ x2+ m3´ x3 => max ,
σp ,
S x i = 1,0 .
3. Сформулируем ЭММ задачи с учетом конкретных исходных данных. Найти вектор Х= (x1, x 2, x 3), максимизирующий доходность портфеля mp.
mp=12´ x 1+10,5´ x 2+11´ x 3 => max
при следующих ограничениях
sp =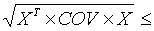 
16
x 1 + x 2 + x 3 =1
x 1, x 2, x 3 ³ 0
Здесь матрица ковариаций так же получена с использованием формулы (4.5) COVi,j= ri,j ´ si ´ sj,
COV=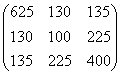
Для решения задачи используется надстройка EXCEL Поиск решения. Исходные данные и расчетные формулы представлены на рис. 4.10.
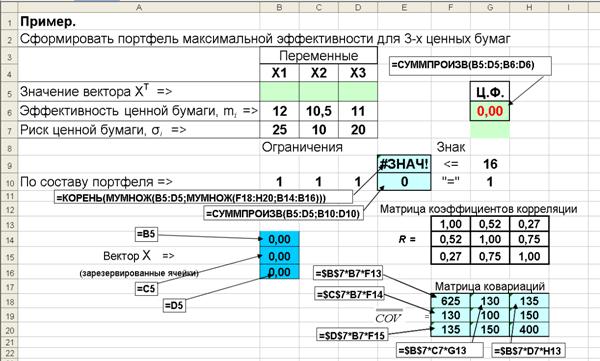
Рис. 4.10. Фрагмент листа Еxcel с исходными данными и расчетными
формулами
В результате решения получена максимально возможная доходность портфеля 11,32 при значениях вектора Х, записанных в ячейки $B5:$D5 (Рис. 4.11.)
Рис. 4.11. Фрагмент листа Еxcel с результатами расчета оптимального портфеля
Ответ: Максимальную доходность 11,29% можно получить, если доли акций R, S и L составят 0,47, 0,28 и 0,25.
Тема 5. Модели оценки доходности финансовых активов
5.1. Основные индикаторы фондовых рынков
Объектом купли-продажи на фондовых рынках одновременно являются акции различных эмитентов с разной степенью доходности.
На рынках ценных бумаг для определения общей тенденции в изменении курсов акций применяются специальные индикаторы – фондовые индексы. Перечень основных биржевых индексов приведен в табл. 5.1.
Таблица 5.1
Основные биржевые индексы мира
Индекс
Страна
Способ
взвешивания
Метод расчета
AEX index
Нидерланды
По капитализации
Среднее взвешенное
ATX
Австрия
По капитализации
Среднее взвешенное
CAC 40
Франция
По капитализации
Среднее взвешенное
DAX
Германия
По капитализации
Среднее взвешенное, суммарный доход на капитал
DJIA
США
По цене
Среднее арифметическое невзвешенный (пропорционально дроблению каждой первоначальной акции)
FTSE
Великобритания
-
-
Nikkei 225
Япония
По цене
Среднее взвешенное
S&P 500
США
По капитализации
Среднее взвешенное
TOPIX
Япония
По капитализации
Среднее взвешенное
ММВБ
Россия
По капитализации
Среднее взвешенное
RTSI
Россия
По капитализации
Среднее взвешенное
Биржевой (фондовый) индекс является обобщенным показателем изменения цен определённой группы активов (ценных бумаг, товаров или производных финансовых инструментов).
Обычно абсолютные значения индексов не важны. Большее значение имеют изменения индекса с течением времени, поскольку они позволяют судить об общем направлении движения рынка, даже когда цены акций внутри «индексной корзины» изменяются разнонаправлено. В зависимости от выборки показателей, биржевой индекс может отражать поведение какой-то группы активов (ценных бумаг) или рынка (сектора рынка) в целом.
Для изучения характера взаимосвязи в изменении фондовых индексов и доходности ценных бумаг строятся рыночные модели, с помощью которых можно оценивать инвестиционные портфели предприятий. Оценить риск финансовых активов можно с помощью модели Шарпа.
Теория рыночной цены финансовых активов включает три составные части:
1) обоснование соответствия структуры каждого индивидуального портфеля рыночному портфелю;
2) основные уравнения модели ценообразования финансовых активов:
- уравнение линии рынка капитала (Capital Market Line - CML),
- уравнение линии рынка ценных бумаг (Capital Asset Pricing Model – CAPM) ,
- уравнение характеристической линии (Security Market Line - SML);
3) проверка соответствия получаемых выводов и результатов реальной хозяйственной практике.
Рассмотрим подробнее методы получения основных моделей ценообразования финансовых активов и проведем их содержательный анализ.
5.2. Уравнение линии рынка капитала (CML)
Для характеристики соотношения между ожидаемым доходом mp и риском индивидуального портфеля каждого инвестора используется уравнение рынка капитала:
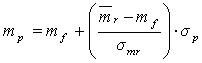(5.1)
где mf – доходность (ставка процента) безрисковых ценных бумаг,
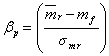- коэффициент при риске портфеля (рыночная цена риска) характеризует прирост ожидаемой доходности рыночного портфеля над безрисковой ставкой процента (премия за риск в среднем по рынку),
mp – ожидаемая доходность портфеля инвестора,
σp – риск (стандартное отклонение доходности) портфеля инвестора,
, σmr – средний ожидаемый доход и риск рыночного портфеля.
Из уравнения (5.1) следует, что ожидаемая доходность оптимального портфеля каждого инвестора превышает безрисковую ставку процента, если ожидаемая доходность рыночного портфеля превышает эту ставку. Графическая интерпретация уравнения линии рынка капитала совместно с линией эффективного множества приведена на рис. 5.1.
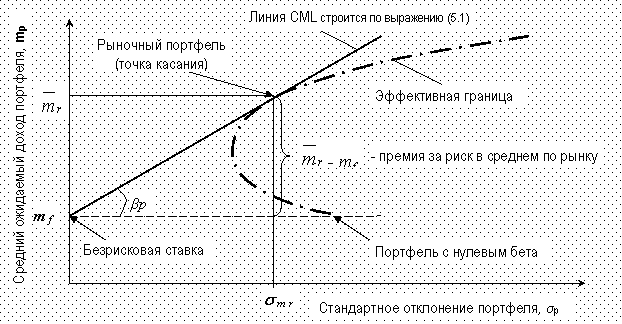
Рис. 5.1. Линия рынка капитала CML и эффективная граница
Из рисунка видно, что ожидаемая доходность и риск каждого оптимального индивидуального портфеля располагаются на одной прямой, которая содержит множество всех эффективных индивидуальных портфелей. Причем сам рыночный портфель принадлежит этому же множеству эффективных портфелей.
Разницу (
- mf ) между ожидаемой доходностью рискового актива индивидуального или рыночного портфеля и безрисковой ставкой процента называют премией за риск. Инвестор не склонный к риску не будет осуществлять рисковые инвестиции, если премия за риск отрицательна.
При положительной премии за риск по рыночному портфелю премия за риск по индивидуальному портфелю каждого инвестора также будет положительной, и наоборот.
Таким образом, согласно уравнению (5.1) можно записать:
Доходность портфеля = Безрисковая ставка + Цена риска ´ Риск портфеля
Модель (5.1) определяет эффективность тех ценных бумаг, которые покупаются и продаются на идеальном рынке. На реальном рынке ценные бумаги могут отклоняться от прямой идеального рынка на величину невязок a. Тогда, если эти отклонения будут находиться над линией (a>0), то теоретическая линия будет занижать возможности ценной бумаги i, если под линией (a<0) то завышать возможности данной ценной бумаги.
Поэтому в портфель, прежде всего, включаются те ценные бумаги, которые недооценены рынком и продаются дешевле
5.3. Рыночная модель оценки капитальных активов Шарпа
Пусть за некоторый период времени изучается взаимосвязь между доходностью определенной совокупности ценных бумаг и доходностью рынка (рыночным индексом) в том же периоде. При этом изменение рыночного индекса может вызывать соответствующее изменение цены i-ой ценной бумаги. Поскольку такие изменения носят случайный характер и взаимосвязаны, то для их отражения используется рыночная модель в виде уравнения регрессии (характеристической линии ценной бумаги):
m i = a i + b i ´ m r+ e i (5.2.)
где mi - доходность ценной бумаги i за период времени t (зависимая переменная);
mr - доходность на рыночный индекс за этот же период (независимая, объясняющая переменная);
a i - коэффициент смещения линии регрессии, характеризует ожидаемую доходность i-ой ценной бумаги при условии нулевой доходности рыночного индекса;
b i - коэффициент наклона, характеризует наклон линии регрессии и является характеристикой риска;
e i - случайная погрешность.
Оценка параметров такой модели (a и b - коэффициентов) обычно производится с помощью известного МНК. Бета - коэффициент (beta coefficient) вычисляется по одной из формул:
=
= 
=
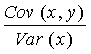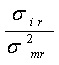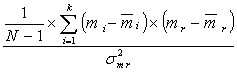. (5.3)
Здесь s i r - ковариация между доходностью акции i-ой бумаги и доходностью на рыночный индекс, а s 2m r - дисперсия доходности на индекс.
Наклон в рыночной модели ценной бумаги отражает чувствительность ее доходности к доходности на рыночный индекс.
Бета-коэффициент оценивает изменения в доходности отдельных акций в сопоставлении с динамикой рыночного дохода, он может быть положительным или отрицательным. Если b >0, то доходность соответствующих ценных бумаг изменяется в том же направлении, что и рыночная доходность. При b < 0 эффективность ценной бумаги и рыночный индекс изменяются в противоположных направлениях.
Коэффициент бета является показателем относительной неустойчивости курса акций по сравнению с остальным рынком. Например, в США для сводного индекса 500 агентства Standard & Poor's b = 1,0; Ценные бумаги, имеющие коэффициент b >1,0 считаются агрессивными и являются более рискованными, чем рынок в целом; для менее рискованных бумаг b <1,0.
Коэффициент бета рассматривается как индекс систематического риска вследствие общих условий рынка. Осторожные инвесторы предпочитают акции с низким уровнем коэффициента бета.
Коэффициент смещения рассчитывается как разность:
a i =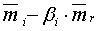 
. (5.4)
Коэффициент детерминации R2 уравнения (5.2) показывает долю рыночного риска в общем риске по данной ценной бумаге, выраженном дисперсией ее доходности.
Для определения параметров уравнения (5.2) необходимо иметь ряды наблюдений доходности отдельных ценных бумаг и ряды доходности на индекс. Такие ряды формируются по результатам котировки акций.
Биржевая котировка акций - рыночная цена акций на фондовой бирже, определяемая соотношением спроса и предложения. Котировка акций - официально публикуется и ее можно найти на различных сайтах в интернете в виде биржевых курсов акций.
Курс акции - отношение рыночной цены акции к ее номинальной, нарицательной стоимости, т. е. цена, по которой акция продается на рынке.
Доходность акции - отношение прибыли, приходящейся на одну обыкновенную акцию к ее рыночной стоимости. Доходность акций зависит от ряда факторов: темпов роста курса акции; размера выплачиваемых дивидендов; темпов инфляции и роста банковского процента; размеров налогов с прибыли. Доход по акции можно рассчитывать по ее известным курсам.
Доход по акции – представляет собой процент прибыли, которую получил бы инвестор купивший акцию в конце некоторого периода времени (дня, недели, месяца, года и др.) t-1 и продавший ее в конце следующего периода t. При этом доход может вычисляться либо в виде непрерывного сложного дохода по выражению:
, (5.5)
либо в виде дискретного дохода
. (5.6)
Здесь m t i , m (t-1)i – курсы i – ой акции в конце текущего (t) и предыдущего (t-1) периодов времени.
Если бы по акции выплачивались дивиденд, то весь доход составил бы
, (5.7)
где div t i – дивиденд, выплачиваемый по i – ой акции на момент времени t.
Доход, подсчитанный как непрерывный сложный процент, всегда будет несколько меньше дискретного сложного процента.
При использовании выражений (5.5, 5.6 и 5.7) следует помнить, что оценка дохода такими методами возможна только в том случае, если данные о доходах в рассматриваемой выборке представляют собой распределение дохода (в вероятностном смысле) в предстоящем периоде.
Пример. 5.1. По данным инвестиционной компании «ФИНАМ» о фактической доходности акций и доходности на индекс РТС (RTSI) за период с января 2008 по май 2009 гг. (http://www. *****/analysis/export/default. asp), см. табл. 5.2.
Таблица 5.2
Индекс РТС и котировки акций на конец месяца
Год
Месяц
RTSI
GAZP
SBER
ROSN
2008
январь
1906,97
290,95
87,89
172,00
2008
февраль
2063,94
304,95
80,2
196,04
2008
март
2053,93
297,61
73,48
211,21
2008
апрель
2122,50
312,49
77,1
231,20
2008
май
2459,88
360,09
85,2
286,90
2008
июнь
2303,34
341,00
74,29
272,60
2008
июль
1966,68
277,89
69,09
247,40
2008
август
1646,14
242,34
57,4
209,00
2008
сентябрь
1211,84
198,00
43,69
171,39
2008
октябрь
773,37
133,50
27,77
123,60
2008
ноябрь
658,14
118,36
23,21
108,50
2008
декабрь
631,89
107,63
22,79
110,29
2009
январь
535,04
114,70
16,44
111,16
2009
февраль
544,58
116,50
14,27
126,10
2009
март
689,63
126,40
20,85
146,59
2009
апрель
832,87
147,82
27,8
176,99
2009
май*
990,26
170,15
39,54
184,11
*) данные за неполный месяц
определить ожидаемую доходность, риск и параметры рыночных моделей (альфа и бета коэффициенты) для акций «Газпром» (GAZP), «Сбербанк» (SBER) и «Роснефть» (ROSN). По результатам расчета построить графики зависимостей доходности акций от доходности на индекс РТС.
Решение
1. На листе Excel вводятся среднемесячные данные по индексу РТС и котировкам акций за указанный период времени, рис.5.2, ячейки (A4:F20).
2. По выражению (5.6) рассчитываются среднемесячные значения доходностей в указанный период, пренебрегая выплатой дивидендов, рис. 5.2, ячейки (G5:J20). Среднемесячный доход по каждой акции представляет собой процент прибыли, которую получил бы инвестор, купивший акцию в конце (t-1) месяца и продавший ее в конце следующего месяца (t).
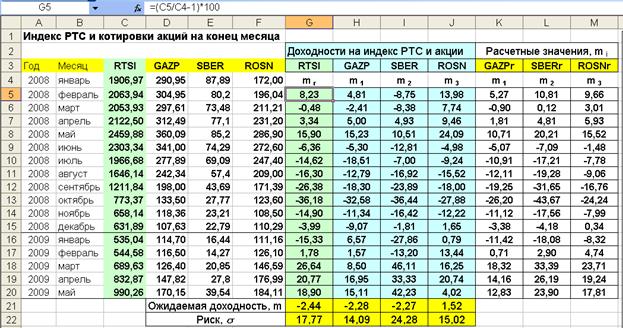
Рис.5.2. Исходные данные и результаты расчета доходностей по котировкам акций и по моделям
3. Используя статистические функции СРЗНАЧ (ячейки G21:J21), рассчитываются средние ожидаемые доходности на индекс РТС и по каждой акции. Затем с помощью функции СТАНДОТКЛОН (ячейки G22:J22) вычисляются значения риска s.
4. Воспользовавшись инструментом «Регрессия» в Пакете анализа рассчитываются параметры моделей по типу (5.2). Фрагменты из стандартного вывода результатов расчета в Excel с дополнительными комментариями приведены ниже.
По результатам расчета параметров (коэффициентов a и b) моделей, можно записать три модели связи доходностей акций с доходностью на индекс РТС:
для акций «Газпрома» m1 = - 0,56 + 0,72 mr ,
для акций «Сбербанка» m2 = 0,72 + 1,23 mr ,
для акций «Роснефть» m3 = 3,38 + 0,76 mr .
Для акций GAZP
Для акций SBER
Для акций ROSN
ВЫВОД ИТОГОВ
ВЫВОД ИТОГОВ
ВЫВОД ИТОГОВ
Регрессионная статистика
Регрессионная статистика
Регрессионная статистика
Множественный R
0,894
Множественный R
0,898
Множественный R
0,903
R-квадрат
0,799
R-квадрат
0,806
R-квадрат
0,816
Нормированный R-квадрат
0,784
Нормированный R-квадрат
0,792
Нормированный R-квадрат
0,802
Стандартная ошибка
6,540
Стандартная ошибка
11,068
Стандартная ошибка
6,677
Наблюдения
16
Наблюдения
16
Наблюдения
16
Коэффициенты для GAZP
Коэффициенты для SBER
Коэффициенты для ROSN
Y-пересечение, a
- 0,56
Y-пересечение, a
0,72
Y-пересечение, a
3,38
Переменная X1, b
0,72
Переменная X1, b
1,23
Переменная X1, b
0,76
Приведенные модели могут быть использованы для прогнозной оценки ожидаемой доходности по акциям данных компаний при изменении доходности по индексу РТС. Так, например, при ожидаемой доходности на индекс РТС 2% доходность по акциям «Газпрома» составит m1 = - 0,56 + 0,72*2 = 0,88%, по акциям «Сбербанка» m2 = 0,72 + 1,23*2 = 3,18% и «Роснефть» m3 =3,38 + 0,76*2 = 4,9% , соответственно.
Как уже упоминалось выше, коэффициент детерминации R2 в полученных моделях отражает доли рыночного риска в общем риске по данной ценной бумаге. С учетом этого доля рыночного риска в общем риске наиболее полно учитывается в модели для акций ROSN поскольку для нее R2 = 0,816 и в меньшей степени в моделях для акций GAZP R2 = 0,799 и акций SBER R2 = 0,806.
5. По полученным в предыдущем пункте моделям вычисляются расчетные значения доходностей, которые затем представляются в виде линейных зависимостей доходностей соответствующих акций от доходности на индекс РТС. На этом же графике, рис.5.3 для проведения сравнения нанесены и фактические значения доходностей, выделены отдельными маркерами.
Из приведенного графика видно, что характеристики всех трех акций имеют положительный угол наклона, причем для акций Сбербанка β = 1,23 (т. е. β > 1,0) поэтому их можно отнести к агрессивным ценным бумагам, поскольку они являются более рискованными, чем рынок в целом.
Для акций Газпрома β = 0,72, он практически совпадает коэффициентом бета для акций Роснефти β = 0,76, поэтому характеристические линии имеют практически один угол наклона, т. е. они почти параллельны друг другу. Подобное расположение линий означает, что с ростом доходности фондового рынка (либо индекса рынка) РТС ожидаемая доходность всех акций возрастает, причем доходность по акциям Сбербанка растет более интенсивно, чем по акциям Газпрома и Роснефти.
В точке пересечения характеристик SBERr и ROSNr ожидаемые доходности по акциям обоих видов совпадают.
Поскольку коэффициенты смещения a i для характеристических линий двух акций (a 2, a 3) положительны, то при нулевой доходности фондового рынка (mr = 0) они обеспечат прибыль по акциям Сбербанка 0,72% и по акциям Роснефти 3,38%. Акции Газпрома имеют отрицательное значение a1= - 0,56, поэтому при тех же условиях (при нулевой доходности РТС) они принесут убыток.
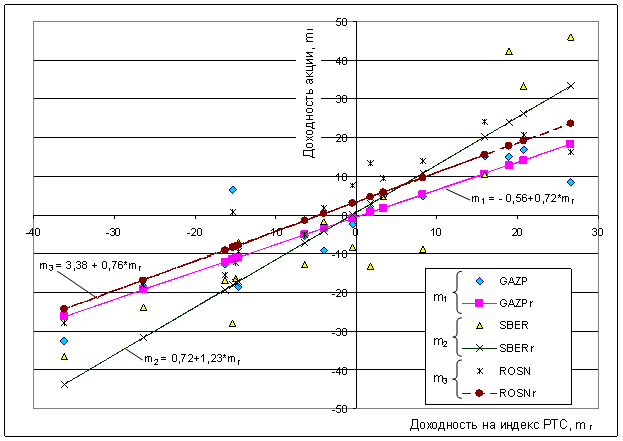
Рис.5.3. Зависимости доходности акций от доходности на индекс РТС
5.4. Определение доли рыночного и нерыночного риска активов
Общий риск ценной бумаги i, измеряемый ее дисперсией si 2, обычно представляют в виде двух составляющих:
- рыночный (систематический или недиверсифицируемый) риск (market risk);
- собственный (несистематический или диверсифицируемый) риск (unique risk).
С учетом этого дисперсию s i2 для ценной бумаги можно записать в виде суммы:
si2 = b i 2s m r2+se2, (5.8)
где b 2i sm r2 - обозначает рыночный риск ценной бумаги i,
se2 - собственный риск ценной бумаги i, мерой которого является СКО случайной погрешности e i в уравнении (5.2). Выражение (5.8) можно интерпретировать так: Общий риск = Рыночный риск + Собственный риск
(систематический) (несистематический)
Или другими словами вариация доходности каждой ценной бумаги состоит из двух слагаемых: «собственной» вариации, не зависящей от рынка, и «рыночной» части вариации, определяемой случайным поведением рынка в целом. При этом отношение b i2s2m r /se2 характеризует долю риска ценных бумаг вносимую рынком, его обозначают Ri2 и называют коэффициентом детерминации. Бумаги с большими значениями Ri2 могут оказаться предпочтительнее, поскольку их поведение более предсказуемо.
Здесь β коэффициент является количественным измерителем систематического риска, не поддающегося диверсификации. Бета - коэффициенты определяются для акций каждой компании котировавшихся на рынке в рассматриваемом периоде.
Ценная бумага, имеющая β-коэффициент равный 1,0 копирует поведение рынка в целом, если b >1, то реакция ценной бумаги опережает изменение рынка и такие акции разумно иметь в своем портфеле, когда ожидается рост доходности рыночного портфеля. В этом случае они могут обеспечить инвестору более высокий уровень доходности, чем в среднем по рынку. Систематический риск такого финансового актива выше среднего. Менее рисковыми являются активы, для которых 0 < β < 1. Если ожидается падение доходности рыночного портфеля, то целесообразно иметь в портфеле акции с коэффициентом меньше единицы, поскольку для них риск меньше риска рыночного портфеля.
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 |
