Точка, не доминируемая никакой другой называется оптимальной по Парето, а множество всех таких точек называется множеством оптимальности по Парето. Выбор лучшей из рассматриваемых операций производится обязательно из операций, оптимальных по Парето.

Для нахождения лучшей операции иногда применяют взвешивающую формулу, которая для пар (`Q, r) дает одно число, по которому и определяют лучшую операцию. Например, пусть взвешивающая формула имеет вид:

j(`Q ) = 2 ×`Q - r . Тогда получаем: j(`Q 1) = 2*4,83 -1,77 = 7,89; j(`Q 2) = 4,75; j(`Q 3)= 11,69; j(`Q 4)= 3,12.

На рис. 3.16. приведена графическая иллюстрация результатов, полученных с помощью взвешивающей формулы.

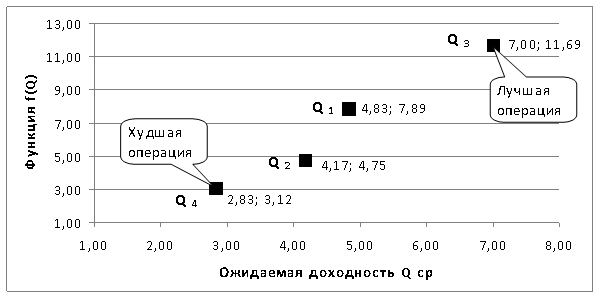
Рис.3.16. Множество операций

Из последнего рисунка видно, что 3-я операция – лучшая, расположена в правом верхнем углу графика, а 4-я – худшая занимает левый нижний угол.

3.6. Экспертные методы оценки риска

Когда из-за отсутствия данных, нельзя использовать количественные методы прогнозирования показателей риска, могут использоваться экспертные методы оценки риска. Задача экспертного оценивания сводится к получению группового субъективного мнения на основе обработки совокупности индивидуальных мнений экспертов.

Методы экспертной оценки риска – совокупность логических и математических процедур позволяющих получать информацию от специалистов-экспертов, проводить ее анализ и обобщать результаты для выбора рациональных решений.

Среди методов экспертных оценок выделяются две группы: коллективные методы оценивания и методы получения индивидуального мнения экспертов.

Коллективные методы оценивания («мозговая атака», деловые игры, сценарии, совещания, «суд») предполагают выработку общего мнения в ходе совместного обсуждения.

Методы получения индивидуального мнения (анкетный опрос, Дельфи, интервью) построены на предварительном сборе информации от опрашиваемых индивидуально экспертов.

Применение экспертных методов оценки риска связано с реализацией следующих этапов:

-  определение цели и задач экспертного оценивания;

-  формирование рабочей группы для управления и проведения экспертного оценивания;

-  выбор метода получения экспертной информации и способов ее обработки;

-  формирование группы экспертов и разработка анкет опроса;

-  опрос экспертов (проведение экспертизы);

-  обработка и анализ результатов экспертизы;

-  интерпретация полученных результатов;

-  составление отчета.

На первом этапе определения цели экспертизы устанавливается признак, по которому производится оценка. Если целей несколько, то оценки по различным шкалам целесообразно свести к единой шкале, например за счет установления цели более высокого уровня.

Методы групповой экспертной оценки делятся на два вида: открытая дискуссия и анкетный опрос.

Метод открытой дискуссии имеет ряд недостатков: не исключается давление авторитетов, затруднена математическая обработка обобщенного мнения группы экспертов и степени их согласованности.

Опрос экспертов с помощью анкет устраняет недостатки методов открытой дискуссии, поскольку свои заключения по поставленным вопросам эксперты представляют анонимно.

Формирование группы экспертов связано с вопросами определения ее качественного и количественного состава.

При качественном отборе к экспертам предъявляются следующие требования: информированность, высокий уровень общей эрудиции, отсутствие личной заинтересованности в результатах экспертизы, глубокие специальные знания в оцениваемой области деловитость и объективность, наличие производственного и (или) исследовательского опыта в данной области и т. д.

Степень компетентности экспертов оценивается одним из двух способов: объективный способ; субъективный способ.

Наиболее часто пользуются субъективными способами, которые в свою очередь делятся на два вида:

взаимооценочные – уровень компетентности экспертов определяется по характеристикам, данных им другими участниками экспертизы;

самооценочные – сам эксперт определяет вес своей оценки по некоторому вопросу, пользуясь оценочной шкалой, представляемой ему прогнозистом.

Второй способ определения компетентности экспертов более простой с точки зрения получения исходных данных, поскольку не требует предварительной обработки данных для получения веса оценки эксперта.

Компетентность эксперта (К) оценивается степенью его квалификации, которая определяется на основе суждений эксперта о своей информированности по решаемой проблеме (Ки) и уровне аргументации своих мнений (Ка): К = 0,5 (Ки + Ка).

Увеличение количества экспертов приводит к снижению погрешности экспертной оценки, но при этом точность прогноза растет медленнее количества экспертов. На практике подбирается компромиссный вариант между требуемой точностью и стоимостью прогноза. Считается, что в состав группы целесообразно включать не менее 5-12 специалистов.

На точность групповых оценок также влияет и степень согласованности ответов экспертов.

Вопросы для экспертов, могут иметь содержательный ответ в развернутой форме или в виде количественной оценки.

В последнем случае возможно применение математических методов обработки результатов.

Метод «Дельфи» реализует анкетный способ опроса при прогнозировании количественных показателей. Для повышения достоверности групповой оценки экспертиза проводится в 3-4 тура. После каждого тура экспертов знакомят с результатами прежнего тура перед началом следующего.

Доверительная вероятность такого прогноза составляет 50%.

3.5.1. Метод «Дельфи»

Рассмотрим алгоритм обработки результатов методом «Дельфи» на конкретном примере.

Пример. 3.9. Десять экспертов оценили прогнозные значения экономического показателя Y. Найти методом «Дельфи» точечный и интервальный прогнозы.

Наименование

Эксперт, j

1

2

3

4

5

6

7

8

9

10

Показатель, x

16,9

13,8

11,9

12,3

16,3

12

16,1

20,6

16,8

13,1

Решение

Алгоритм обработки результатов методом «Дельфи» содержит следующие этапы.

1. Результаты оценок экспертов ранжируются в порядке возрастания.

11,9

12,0

12,3

13,1

13,8

16,1

16,3

16,8

16,9

20,6

2. Определяется количество интервалов (N) между первым и последним значениями ранжированного ряда. Для данных условий между первым и последним значением ряда находится 9 интервалов.

3. Рассчитывается количество интервалов приходящихся на один (N/4), два (N/2) и три (ЗN/4) квартиля, соответственно: на один квартиль: 9/4 = 2,25 интервала, на два квартиля - 4,5 и на три 6,75 интервалов, соответственно.

4. Для нахождения первого квартиля Q1 смещаемся от первого члена ряда на 2 интервала и получаем значение 12,3. к этому значению надо добавить число, равное произведению 0,25 на разность (13,1-12,3). Таким образом, имеем

нижняя граница доверительного интервала будет равна:

 

точечный прогноз показателя:

верхняя граница доверительного интервала:

 

3.5.2. Метод статистической обработки результатов экспертизы

Алгоритм данного метода включает расчет следующих показателей.

1.  Рассчитывается точечная оценка результатов экспертных оценок Bi, полученных при опросе экспертов на основе средней арифметической

 

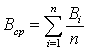
, (3.18)

где Bi – значение прогнозируемой величины, данное i-м экспертом;

n – число экспертов в группе.

2.  Определяется дисперсия:

 

,

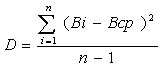
(3.19)

3.  Рассчитывается приближенное значение доверительного интервала

 

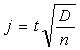
(3.20)

где t – коэффициент Стьюдента для заданного уровня значимости и числа степеней свободы k = n – 2.

4.  Определяются доверительные границы для прогнозируемого показателя:

– для верхней границы Ав=Вср+ j ,

– для нижней границы Ан=Вср – j .

Пример. 3.10. Десять экспертов оценили прогнозные значения показателя риска Bi. Найти методом статистической обработки результатов точечный и интервальный прогнозы. Коэффициент Стьюдента выбрать для уровня значимости α=0,40.

Решение

Расчеты производятся по соответствующим формулам приведенного выше алгоритма. Исходные данные, расчетные формулы и результаты расчета представлены на листе Excel, рис. 3.17

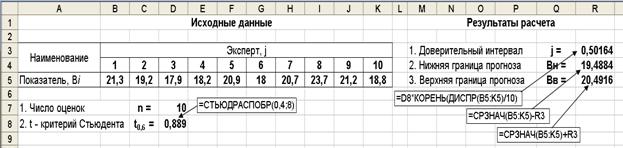
Рис. 3.17. Исходные данные, расчетные формулы и результаты расчета

3.5.3. Оценка согласованности мнений экспертов

Степень согласованности мнений экспертов, как упоминалось выше, влияет на точность результатов проводимой экспертизы. При низкой согласованности мнений экспертов проводится содержательный анализ их оценок с целью выявления причин значительного различия в оценках. Если это объясняется недобросовестностью экспертов, то следует повторить экспертный опрос.

Оценка степени согласованности экспертов может проводиться с помощью различных методов: коэффициента вариации, коэффициента ранговой корреляции Спирмена, коэффициента конкордации и др.

Коэффициент вариации используется при оценках в физических единицах величин, бальных оценках, попарных сравнениях. Он характеризует относительную степень разброса мнений экспертов по отношению к среднему значению коллективной оценки. Степень согласованности мнений экспертов считается удовлетворительной, если коэффициент вариации не превышает значения 0,30 и хорошей когда коэффициент вариации не более 0,20.

Коэффициент ранговой корреляции Спирмена может использоваться для оценки меры близости ранжировок, выполненных двумя экспертами. При отсутствии одинаковых рангов в ранговом ряду коэффициент ранговой корреляции рассчитывается по формуле:

 

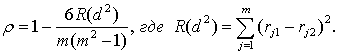
(3.21)

Здесь rj1, rj2 – ранги, полученные j-м элементом от 1 и 2-го экспертов соответственно; dj = rj1 – rj2 – разности между рангами поставленными экспертами; m – количество ранжируемых элементов.

Чем меньше разности между рангами, тем больше будет r и тем ближе его значение будет к +1,0. Если корреляция отсутствует, то все ранги будут перемешаны и между ними не будет никакого соответствия, тогда значение r окажется близким к 0.

Ограничения по применению коэффициента: количество ранжируемых элементов в каждой выборке должно быть от 5 до£ m £ 40); при большом количестве одинаковых рангов по одной или обеим выборкам коэффициент r дает приближенные значения (идеальным считается вариант, когда оба коррелируемых ряда представлены несовпадающими рангами), поэтому делается поправка на одинаковые ранги.

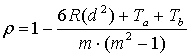, (3.22)

где 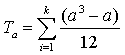, - поправки.

Здесь a, b – объемы каждой группы одинаковых рангов в первом и втором ранговом ряду соответственно; k, l – количество групп с одинаковыми рангами в первом и втором ряду.

Для данного m по таблице (см. приложение 1) определяется критичесское значение rкр. Если рассчитанное значение r ³ rкр , то корреляционная связь между двумя ранговыми рядами будет достоверна при заданном уровне значимости a.

Пример. 3.11. Два эксперта проранжировали шесть (m = 6) факторов риска (Х1,Х2,…,Х6) по степени их важности. Оценить меру близости ранжировок, выполненных экспертами с помощью коэффициента ранговой корреляции Спирмена при уровне значимости a = 0,05. Исходные данные представлены на рис. 3.18.

Решение

1. Рассчитываются квадраты отклонений d2 в оценке по каждому i-му показателю, ячейки В7:G7, рис. 3.18.

2. Вычисляется сумма квадратов по всем отклонениям в оценках экспертов R(d 2), ячейка J5.

3. Определяется фактическое значение коэффициента ранговой корреляции по формуле (3.22), которое равно r = 0,771, ячейка J6.

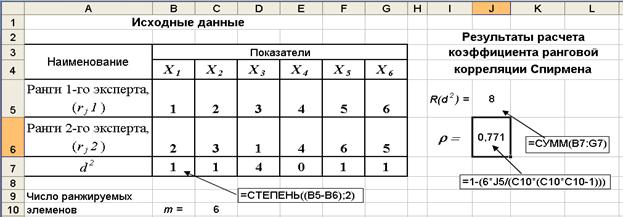
Рис. 3.18. Результаты расчета коэффициента ранговой корреляции Спирмена

4. Рассчитанное значение коэффициента ранговой корреляции сравнивается с критическим значением rкр = 0,65 - для шести наблюдений (m = 6) и уровня значимости a = 0,05 (см. Приложение 2). Поскольку r ³ rкр то это означает, что мнения экспертов в оценке шести показателей в основном совпадают и результатам такой экспертизы можно доверять.

Коэффициент конкордации позволяет определить степень согласованности мнений экспертов по всем оцениваемым объектам, когда число экспертов более двух.

Коэффициент конкордации рассчитывается по следующей схеме.

1. Вычисляется сумма рангов, полученных j-м элементом от всех экспертов:

 

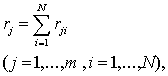
(3.23)

где rj i – ранг, полученный j-м элементом от i-го эксперта;

N – количество экспертов, принимающих участие в экспертизе.

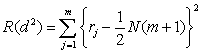2. Рассчитывается величина R(d 2):

. (3.24)

3. Рассчитывается максимально возможное значение Rm(d 2), для идеального случая, когда ранжировки всех экспертов совпадают:

(3.25)

4. Вычисляется значение коэффициента конкордации W, как отношение полученного значения R(d 2) к максимально возможному Rm(d 2).

 

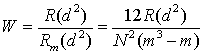
(3.26)

Коэффициент конкордации W принимает значения от 0 до 1,0. При W=1,0 имеет место полная согласованность мнений экспертов, при W > 0,5 – удовлетворительная и при W < 0,5 – низкая.

Поскольку оценки экспертов считаются случайными величинами, то целесообразно проводить проверку значимости коэффициента W, путем определения вероятности согласованности их мнений с помощью распределения c2 : c 2 = N (m-1) W £ c 2табл (a, k) , (3.27)

где a – уровень значимости,

k = m -1– число степеней свободы.

Пример. 3.12. Шесть экспертов (N=6) ранжируют пять (m=5) элементов (Х1,Х2,…,Х5) по их важности. Результаты приведены в таблице. Определить суммарную ранжировку этих элементов и коэффициент конкордации. Проверить значимость коэффициента конкордации, если табличное значение c 2 для 1% уровня значимости и 4-х степеней (n = m-1 = 5-1 = 4) свободы равно 13,28.

Решение

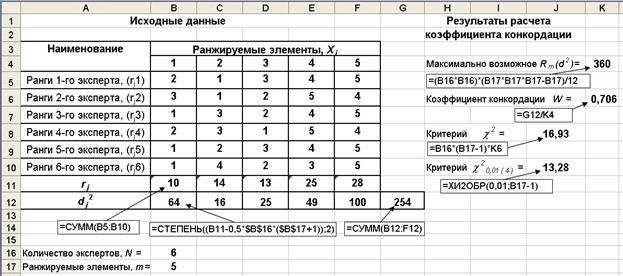
Рис.Исходные данные, расчетные формулы и результаты расчета коэффициента конкордации

1. По каждому j-му столбцу рассчитывается значение rj , по формуле (3.23), см. ячейки (B11:F11) табл. на рис. 3.19.

2. По формуле (3.24) рассчитывается величина R(d 2), для этого предварительно вычисляются частные значения d j2 (см. ячеки (B12:F12)) и затем эти значения суммируются в ячейке G12, значение R(d 2) = 254.

3. Рассчитывается максимально возможное значение величины Rm(d 2) с использованием формулы (3.25), оно находится в ячейке K4 и составляет Rm(d 2) = 360.

4. Рассчитывается коэффициент конкордации W по формуле (3.26), он принимает значение равное 0,706, которое находится в ячейке K6. Чем ближе значение W к единице, тем сильнее согласованность между экспертами.

5. Проверяется значимость рассчитанного коэффициента W по критерию c 2. С этой целью вначале вычисляется значение c 2 для фактических значений, по формуле (3.27), оно находится в ячейке J8 и составляет 16,93.

Затем с помощью статистической функции Excel ХИ2ОБР для заданного в условии уровня значимости и k=4 степеней свободы определяется табличное значение критерия c 2кр = 13,28.

Далее проводится сравнение фактического значения c 2 =16,93 с критическим c 2кр = 13,28, и поскольку выполняется неравенство c 2 >c 2кр , то можно сделать вывод об удовлетворительной согласованности мнений экспертов в оценке ранжируемых элементов.

Тема 4. Основы формирования оптимальных инвестиционных портфелей

4.1. Основные характеристики портфеля ценных бумаг

Если предприятие располагает достаточным резервом финансовых средств, то оно само может стать инвестором, т. е. вкладывая финансовые средства в ценные бумаги других организаций, оно может получать дополнительную прибыль. Процесс инвестирования характеризуется временем, доходностью и риском. Вложив финансовые средства сейчас, возможное вознаграждение наступает позже и его величина обычно заранее неизвестна.

Такие операции связаны с формированием инвестиционных портфелей, оценка эффективности которых производится по показателям доходности и риска. В связи с этим рассмотрим основы формирования и управления такими портфелями и методы оценки их эффективности. Управление инвестициями представляет собой управление денежными средствами.

Различают реальные и финансовые инвестиции. Реальные инвестиции обычно включают инвестиции в материально осязаемые активы (земля, оборудование, заводы и пр. активы), а финансовые инвестиции представляют собой контракты, оформленные на бумаге (акции облигации и пр.).

Процесс управления инвестициями обычно включает пять этапов:

1) формулирование инвестиционных целей,

2) формирование инвестиционной политики для достижения выбранных целей,

3) выбор портфельной стратегии с учетом выбранных инвестиционных целей и политики,

4) выбор активов, которые предстоит включить в состав портфеля,

5) измерение и оценка эффективности инвестиций.

Портфель – это совокупность инвестиций в ценные бумаги, обращающихся на финансовом рынке, обеспечивающая достижение инвестиционной цели вкладчика. В состав портфеля могут включаться бумаги только одного типа (акции или облигации) или различного типа (акции, облигации, депозитные и сберегательные сертификаты и т. д.).

Портфельный менеджмент рассматривает принципы формирования инвестиционного портфеля ценных бумаг. Методология инвестиционного менеджмента начала складываться в двадцатые годы прошлого столетия с появлением понятия <истинной> цены (fair price) акции. Задача инвестора состоит в приобретении недооцененных ценных бумаг, рыночная цена которых на момент покупки ниже истинной, и избавлении от переоцененных бумаг, тем самым в перспективе инвестор получает прибыль.

Основы теории финансового портфеля были заложены в статье Гарри Марковица «Выбор портфеля» (1952), в которой он предложил математическую модель формирования оптимального портфеля ценных бумаг и методы построения таких портфелей при определенных условиях. Такая оптимизационная задача относится к классу задач квадратической оптимизации при линейных огра­ничениях. К настоящему времени подобные оптимизационные задачи вместе с задачами линейного програм­мирования имеют эффективные ал­горитмы их решения, в том числе в среде Excel.

Затем в работах Вильяма Шарпа (1964) и Джона Литнера (1965) были введены понятия систематического (рыночного) и несистематического рисков ценной бумаги.

Риск (общий риск) ценной бумаги состоит в неопределенности ее дохода на конец периода инвестирования. Количественно риск измеряется дисперсией доходности ценной бумаги за определенный интервал времени, например, месяц, квартал, год и т. д.

Систематический или рыночный риск акции - это та часть общего риска, которая зависит от факторов, общих для всего рынка ценных бумаг. К ним относятся неожиданные изменения макроэкономических показателей (ВВП, скорость промышленного роста, собираемость налогов, процентная ставка, уровень инфляции и т. д.), изменение политической ситуации в стране или в мире, психологический настрой участников рынка и др.

Несистематический, или собственный риск - это часть общего риска, зависящая только от состояния дел в данной компании, которое характеризуется неожиданными изменениями таких факторов, как вероятность смены руководства, наличие долгосрочных договоров, просроченной дебиторской или кредиторской задолженности, показатели финансового состояния и др.

Математически разделение рисков обычно проводится с помощью уравнения линейной регрессии, связывающего доходность акции с доходностью по рыночному индексу.

Коэффициент регрессии называется коэффициентом бета ценной бумаги и является характеристикой ее рыночного риска. В качестве рыночного обычно берется индекс, достаточно полно отражающий состояние дел в экономике в целом и включающий курсы акций крупных компаний в различных секторах рынка. Обычно за основу расчета индекса берется капитализация входящих в него ценных бумаг.

Общий риск ценной бумаги может представляться не только в виде суммы собственного и несобственного рисков, но и в виде суммы трех слагаемых, где в качестве третьей компоненты выступает риск отрасли, к которой относится компания или в виде многофакторных моделей.

Главная цель в формировании портфеля для инвестора - достижение оптимального сочетания между риском и доходом, т. е. набор инвестиционных инструментов призван снизить до минимума риск его потерь и одновременно максимизировать его доход.

Для получения количественных характеристик инвестиционного портфеля могут использоваться следующие показатели:

1. Доходность портфеля (mp) ценных бумаг - взвешенная средняя из ожидаемых доходов по каждому из компонентов

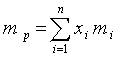(4.1.)

где xi - доли инвестиций (портфельные веса), помещенных в каждый из видов активов записываются в виде вектора XT = (х1, х2, … хn);

mi - ожидаемая ставка дохода по каждому виду активов.

2. риск портфеля - sp - стандартное отклонение ставок дохода по портфелю, рассчитывается как квадратный корень из дисперсии портфельного дохода (вариации Vp), которая определяется по формуле:

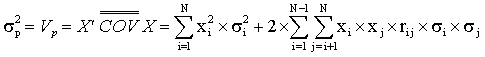, (4.2.)

где - ковариационная матрица порядка N.

Ковариация - это статистическая мера взаимодействия двух случайных переменных, например, доходности двух ценных бумаг.

Положительное значение ковариации показывает, что доходности этих ценных бумаг имеют однонаправленную тенденцию изменения. Ковариация будет низкой, если колебания доходности двух активов носят случайный характер, либо колеблемость одного из них невелика. Ковариация между двумя акциями x и y рассчитывается следующим образом:

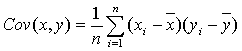. (4.3)

Поскольку содержательная интерпретация численного значения ковариации достаточно сложна, то для измерения силы связи между двумя переменными чаще используется коэффициент корреляции. Этот коэффициент стандартизирует ковариацию путем деления ее на произведение соответствующих средних квадратических отклонений и позволяет привести величины к сопоставимому виду.

Коэффициент корреляции между двумя переменными i и j можно рассчитать по выражению:

r i,j = i, j / s i ´s j , (4.4)

Знак коэффициента корреляции совпадает со знаком ковариации. Его положительные значения соответствуют изменению переменных в одном направлении, а отрицательные – в противоположных направлениях. Если значение r i,j близко к нулю, то связь между переменными слабая. Коэффициент корреляции изменяется в интервале от – 1,0 до +1,0.

В реальных условиях могут проявляться частные случаи:

1)  совершенная положительная корреляция (рис. 4.1.а), например, при приобретении двух видов обычных акций одной корпорации, выпущенных на одинаковых условиях, когда одна из двух ценных бумаг имеет относительно высокую доходность, то и другая ценная бумага так же будет иметь относительно высокую доходность. В этом случае стандартное отклонение ставок дохода по портфелю рассчитывается как средневзвешенная из стандартных отклонений доходов, входящих в состав портфеля активов.

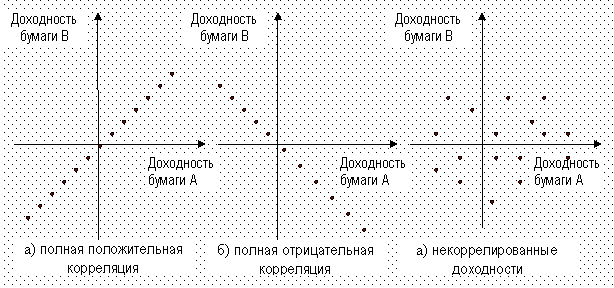
Рис. 4.1. Варианты взаимосвязи доходностей двух ценных бумаг A и B

2)  совершенная отрицательная корреляция (рис. 4.1.б) проявляется в том, что с уменьшением дохода на один пункт по одной акции происходит увеличение дохода на один пункт по другой акции и наоборот. В этом случае инвестор может уменьшить стандартное отклонение дохода по этим двум активам вместе до нуля, т. е. свести риск к минимуму.

3)  отсутствие коррелированной доходности (рис. 4.1.в) означает, что невозможно установить взаимосвязь между ценными бумагами.

Последняя формула может использоваться для расчета ковариации:

i, j = ri, j ´s i ´s j , (4.5)

где s i , s j – стандартные отклонения доходов по i-му и j-му активам, соответственно,

ri j – коэффициент корреляции доходов между i-м и j-м активами.

4.2. Понятие множества эффективных портфелей

Процедура выбора оптимального портфеля включает два независимых решения:

1) определение эффективного множества портфелей;

2) выбор из эффективного множества единственного портфеля, наилучшего для отдельного инвестора.

Зная статистику основных характеристик ценных бумаг (их доходы за определенный период времени) включаемых в состав портфеля можно сформировать эффективный портфель.

Эффективный портфель – это портфель подверженных риску ценных бумаг (активов), дисперсия доходов по которому минимальна среди всех портфелей, имеющих один и тот же средний ожидаемый доход, т. е. эффективный портфель дает максимальный средний доход из всех портфелей с одинаковой дисперсией.

Эффективной границей называется множество всех эффективных портфелей. В 1972 году Блэком было показано, что эффективная граница является выпуклой линейной оболочкой любых двух эффективных портфелей. С учетом этого зная два эффективных портфеля можно найти всю эффективную границу.

Соотношение между ожидаемой доходностью mp и риском портфеля σp из двух рисковых активов A и B при известном коэффициенте корреляции (mA =29,47; mB=59,60; σA = 4,75; σB =11,63; rAB = 0,485) приведено на рис. 4.2.

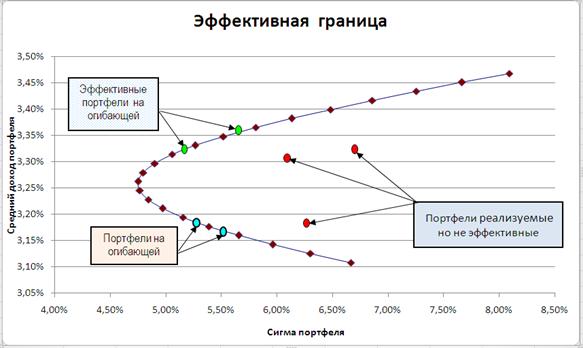
Рис. 4.2. Графическая иллюстрация эффективной границы

и возможных составов портфелей

На рисунке показано, что все выпуклые линейные комбинации лежат на огибающей, но необязательно они являются эффективными. Портфели, лежащие слева от эффективной границы использовать невозможно, поскольку они не принадлежат допустимому множеству. Портфели, лежащие справа от границы (внутренние портфели), являются неэффективными, поскольку существуют другие портфели, которые при заданном уровне риска обеспечивают более высокую доходность, либо более низкий риск для данного значения доходности.

Таким образом, эффективное множество содержит те портфели, которые обеспечивают и максимальную ожидаемую доходность при фиксированном уровне риска, и минимальный риск при заданном уровне доходности.

При расчете эффективной границы для двух активов (A и B) используются следующие соотношения:

средний доход от портфеля рассчитывается по формуле:

mp = g * mA +(1-g) * mB ;

дисперсия доходов от портфеля рассчитывается по формуле:

σp2 = g 2 * σ2A +(1-g)2 * σ2B+2 * g * (1-g) * rAB * σA * σB .

Здесь mA и mB – ожидаемые доходности рискованных активов, rAB - коэффициент парной корреляции между этими активами, σ2A и σ2B – дисперсии;

g и (1-g) – доли активов A и B, соответственно.

Для выбора оптимальных портфелей строятся кривые безразличия инвесторов, которые учитывают отношение инвесторов к риску и доходности. Оптимальный портфель с точки зрения инвестора находится в точке касания эффективного множества портфелей и одной из кривых безразличия.

Пример. 4.1. В состав портфеля включены два вида ценных бумаг: акции (x1) с ожидаемой доходностью m1 = 12% и облигации (x2) с доходностью m2 = 5,1%. Стандартное отклонение акций составляет σ1 = 21,2%, облигаций σ2 = 8,3%. Варьируя портфельными весами активов, необходимо выбрать оптимальную его структуру с точки зрения, применяемого типа активов. Расчеты выполнить для пяти значений коэффициентов парной корреляции rij = -1,0; -0,7; 0; 0,18; 1,0.

Решение

Решение данной задачи удобнее вести в среде Excel, для этого строится вспомогательная таблица, с варьированием удельных весов активов, при этом состав портфеля изменяется с интервалом 0,05 или 5%.. Формат таблицы, расчетные формулы и результаты расчета приведены на рис. 4.3.

Расчет mp ожидаемых доходов портфелей при различных удельных весах активов производится по формуле (4.1) средней арифметической взвешенной, в частности для двух активов данная формула имеет следующий вид

mp = x 1 · m 1+ x2 · m 2 .

Стандартные отклонения σp портфелей при различных коэффициентах корреляции (rij = -1,0; -0,7; 0; 0,18; 1) и удельных весах активов в составе портфеля рассчитываются по формуле:

.

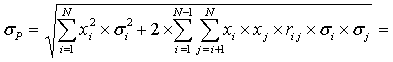
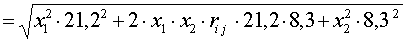По результатам расчета на графике зависимости ве­личины среднего ожидаемого дохода mp от стандартного отклонения σp строятся эффективные границы при соответствующих значениях коэффициентов корреляции, рис. 4.4.

Анализ результатов расчета (рис. 4.3) и графика зависимости средней доходности от стандартного отклонения (рис. 4.4) позволяет сделать следующие выводы:

1. Портфель 0 состоит только из облигаций и имеет ожидаемый доход равный mp = 5,1% со стандартным отклонением портфельного дохода равным sp = 8,3%, тогда как портфель 21 включает только и имеет ожидаемый доход в 12%, а стандартное отклонение 21,2%.

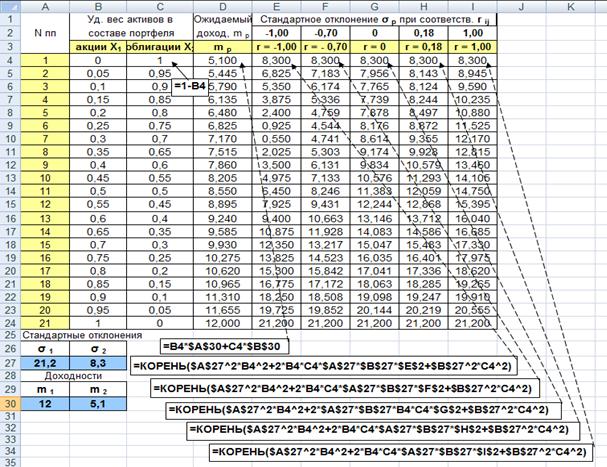
Рис 4.3. Исходные данные и результаты расчета оптимального портфеля в среде Excel

2. Портфель 13, состоящий на 60% из акций и на 40% из облигаций, будет иметь ожидаемый доход в 9,24%, стандартное отклонение дохода по такому портфелю составит 13,71%, если корреляция между изменениями доходов по облигациям и акциям равна (r = 0,18).

3. Если изменения доходов по облигациям и акциям характеризуются совер­шенной положительной корреляцией (r = 1,00), то ожидаемый доход останется прежним, а стандартное отклонение будет включать 60% разности между более высоким стандартным отклонением дохода по акциям и стандартным отклонением дохода по облигациям.

4. В связи с тем, что корреляция между изменениями доходов по облигациям и по акциям не является совершенной, меньшими оказываются и значе­ния стандартного отклонения портфельного дохода.

5. Если представлен­ные облигации могут служить идеальным средством хеджирования вложений в акции или, другими словами, корреляция между измене­ниями доходов по облигациям и акциям оказывается совершенной отрицательной (r = -1,00), то стандартное отклонение порт­фельного дохода будет равно только 9,4%. В этом случае можно сфор­мировать портфель, состоящий на 28% из вложений в акции и на 72% - в облигации (портфель 6), у которого стандартное отклонение порт­фельного дохода практически равняется нулю. Это означает, что с ве­роятностью, равной единице, указанный портфель будет иметь сово­купный доход, составляющий 7,03%.

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8