Кривые доходности используют купонные облигации. Несмотря на то, что срок погашения купонных облигаций известен, на их доходность к погашению воздействуют купонные выплаты (т. н. «купонный эффект»). В этой связи, значения процентных ставок, задаваемых кривой доходности, не полностью соответствует тем, которые предполагает кривая терминальной зависимости. Поэтому при вычислении форвардных ставок необходимо для более точных оценок использовать спот-ставки. Доходность к погашению – это средняя величина нормы отдачи, которую может обеспечить облигация, если она будет сохраняться инвестором до погашения. Это – комплексная средняя величина спот-ставок, применяемых для дисконтирования денежных потоков. Если спот-ставки возрастают, то доходность к погашению сначала превосходит соответствующие спот-ставки, а затем становится ниже их.
На значения процентных ставок в краткосрочном периоде значительное воздействие оказывает проводимая государством кредитно-денежная политика, в то время как долгосрочный сегмент рынка больше подвержен воздействию инфляции. В этой связи выпуклая терминальная кривая может объясняться жесткой монетарной политикой государства (в краткосрочном периоде кривая возрастает, т. к. сжатие денежной массы повышает процентные ставки) и надежным контролем над инфляцией (участники рынка не повышают своих требований к будущим процентным ставкам).
Теории терминальной структуры привлекают внимание и теоретиков, и практиков. Однако, отсутствует согласие в оценке, какая из этих теорий более точно описывает кривые терминальной зависимости. В целом, все сходятся на мнении, что такая зависимость определяется многими факторами, в том числе ожиданиями, желанием избежать риска и сегментацией рынка.
Тема 4
Волатильность и дюрация облигаций.
Свойства волатильности и дюрации.
Как указывалось, отдача облигации в общем случае содержит три составляющие – цену реализации, сумму купонных выплат и сумму процента на процент. Несмотря на большое значение второй и третьей составляющей, все же основная часть отдачи большинства краткосрочных и среднесрочных облигации приходится на цену ее реализации. Поэтому, прежде чем перейти к формированию и управлению портфелем облигаций, необходимо раскрыть основные факторы, влияющие на колебания их цен.
4.1. Волатильность цены облигаций.
Если инвестор приобрел какую-то конкретную облигацию, то по условиям выпуска эмитент не имеет право изменять параметры облигации – ее номинал ![]() , купонную ставку
, купонную ставку ![]() , срок погашения
, срок погашения ![]() (определяемый числом n лет до погашения), а также сколько раз m в год выплачиваются купонные суммы. Тогда единственным переменным фактором, влияющим на изменения цены приобретенной облигации, является доходность к погашению i. Ее колебания происходят под воздействием рыночных факторов на микро - и макроуровне.
(определяемый числом n лет до погашения), а также сколько раз m в год выплачиваются купонные суммы. Тогда единственным переменным фактором, влияющим на изменения цены приобретенной облигации, является доходность к погашению i. Ее колебания происходят под воздействием рыночных факторов на микро - и макроуровне.
В таком случае, под волатильностью (изменчивостью) цены облигации понимается реакция цены облигации на мгновенное, скачкообразное изменение ее доходности к погашению при прочих равных условиях.
Свойства волатильности. Реакция цены облигации на изменение доходности к погашению имеет ряд характерных черт, что и определяет основные свойства волатильности:
1) Зависимость между доходностью к погашению ![]() и рыночной ценой облигации
и рыночной ценой облигации ![]() носит обратный характер. При этом, с понижением величины
носит обратный характер. При этом, с понижением величины ![]() приращения
приращения ![]() при одних и тех же снижениях доходности к погашению
при одних и тех же снижениях доходности к погашению ![]() увеличиваются (рисунок 3):
увеличиваются (рисунок 3):
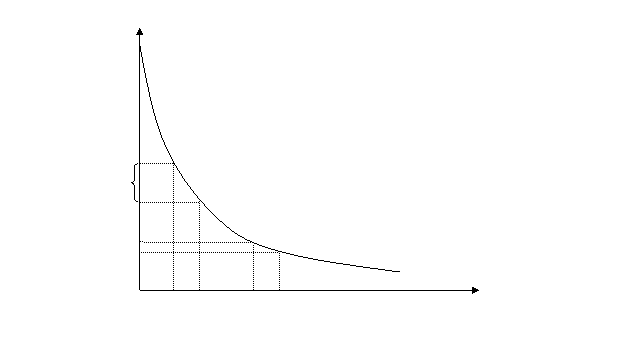
Цена облигации Р0
ΔP1
ΔP2
Δi1 Δi2 доходность к
погашению i
Рисунок 3. Зависимость цены облигации ![]() от ее доходности
от ее доходности
к погашению ![]()
Кривая такой зависимости имеет вогнутость по отношению к началу координат. При снижении доходности к погашению i одним и тем приращениям величины i (Δi1= Δi2) соответствуют более высокие приросты цены облигации ΔP1 > ΔP2.
2) Для одного и того же срока погашения облигации, чем выше купонная ставка, тем слабее реагирует цена облигации на одни и те же изменения доходности к погашению. Соответственно, чем ниже купонная ставка, тем сильнее реакция цены P0 на одни и те же изменения доходности к погашению.
3) Если купонная ставка процента не меняется, то увеличение срока погашения облигации вызывает более сильную реакцию цены ![]() облигации на одни и те же изменения ее доходности к погашению.
облигации на одни и те же изменения ее доходности к погашению.
4) Небольшие изменения доходности к погашению приводят к одинаковым изменениям цены облигации в обоих направлениях. Иными словами, если доходность ![]() возрастает на незначительную величину, то это приводит к такому процентному уменьшению цены
возрастает на незначительную величину, то это приводит к такому процентному уменьшению цены ![]() , которое приблизительно будет равно процентному повышению
, которое приблизительно будет равно процентному повышению ![]() при таком же незначительном снижении
при таком же незначительном снижении ![]() .
.
5) Значительные изменения доходности к погашению ![]() вызывают асимметричную реакцию цен облигации: если доходность к погашению возрастает на несколько процентов (например, 2%), то вызванное этим снижение цены облигации будет в процентном отношении меньше процентного приращения цены облигации при снижении доходности к погашению на те же 2%.
вызывают асимметричную реакцию цен облигации: если доходность к погашению возрастает на несколько процентов (например, 2%), то вызванное этим снижение цены облигации будет в процентном отношении меньше процентного приращения цены облигации при снижении доходности к погашению на те же 2%.
Объяснение подобной реакции цен облигации лежит в нелинейном характере зависимости ![]() от
от ![]() и вогнутом виде кривой этой зависимости (рис.3): когда изменения
и вогнутом виде кривой этой зависимости (рис.3): когда изменения ![]() идут в сторону приращения, то мы попадаем на более пологий участок кривой, поэтому цена уменьшается на не слишком большие величины. Если же
идут в сторону приращения, то мы попадаем на более пологий участок кривой, поэтому цена уменьшается на не слишком большие величины. Если же ![]() сокращается, то мы перемещаемся в область резкого повышения кривой, поэтому и скачки цен в этом случае выше.
сокращается, то мы перемещаемся в область резкого повышения кривой, поэтому и скачки цен в этом случае выше.
6) При заданной величине изменения доходности к погашению ![]() , чем ниже исходная доходность к погашению, тем выше реакция цены на изменения
, чем ниже исходная доходность к погашению, тем выше реакция цены на изменения ![]() .
.
Суммируя все шесть свойств волатильности цены облигации, можно заметить, что на нее большое влияние оказывают пять факторов:
а) исходный уровень доходности к погашению;
б) размах изменений доходности к погашению;
в) направления этих изменений;
г) величина купонной ставки;
д) срок погашения.
При построении портфеля из облигаций инвестор может воздействовать только на последние два фактора, поскольку первые три формируются рыночными условиями и определяются на макроэкономическом уровне. В этой связи важным становится найти способ, с помощью которого можно было оценить влияние купонной ставки и срока погашения облигации на изменения ее цены. Подобные оценки удается сделать с использованием категории дюрации (длительности) облигаций.
4.2. Дюрация облигаций: понятие и основные свойства.
Категория дюрации была введена в экономическую теорию и практику в 1938 году американским экономистом Ф. Маколи (Frederick R. Macauley). Он показал, что дюрация является более приемлемой мерой временного элемента облигации, чем срок ее погашения, ибо дюрация учитывает не только полное возмещение инвестиционных затрат в срок погашения, но также размеры поступления купонных выплат, происходящих до погашения.
Принято считать, что дюрация характеризует “средний срок погашения” всего потока денежных выплат, обеспечиваемых облигацией. Сам Маколи определял дюрацию как “средний взвешенный срок погашения денежных потоков облигации, где “весами” служат приведенные стоимости этих потоков денег”. Иными словами, если известны временные моменты t1, t2, t3, ... tn, после которых инвестор получает купонные выплаты С1, С2, С3, ... Сn и номинал Mn, то дюрация - это средневзвешенная величина этих промежутков времени по долям цены Pi, которую вносит соответствующий денежный поток (купонная выплата и номинал) в начальную стоимость P0 облигации.
Дюрация любой облигации высчитывается по формуле:
![]() (4.1)
(4.1)
где: ![]() - рыночная цена облигации;
- рыночная цена облигации;
t - период времени, в течение которого поступает денежный поток, t=1, 2, ... , n лет; денежный поток в момент t составляют купонные выплаты Ct и номинал ![]() ;
;
n - количество лет, в течение которых поступают купонные выплаты;
i - годовая доходность к погашению.
Иными словами,
![]() (4.2)
(4.2)
Оценим дюрацию бескупонных облигаций. Поскольку для этих облигаций все величины ![]() = 0, то:
= 0, то:
![]()
Следовательно, дюрация бескупонных облигаций всегда равняется сроку погашения этой облигации - n лет.
Сложнее вычислить дюрацию для купонной облигации. Предположим, что инвестор желает определить дюрацию купонной облигации E номинальной стоимостью 1000 руб., сроком погашения 5 лет, с купонным процентом 7%, выплачиваемым ежегодно, и доходностью к погашению ![]() = 5%. Цена такой облигации:
= 5%. Цена такой облигации:
![]() руб.
руб.
Для вычисления D найдем факторы дисконта и приведенные стоимости потоков денег, обеспечиваемых облигацией (в таблице данные по потокам денег приведены в рублях):
Таблица 7.
Расчет дюрации облигации
Годовой
период
Потоки
денег
Фактор
дисконта
при i=5%
PV потоков
денег
(2)(3)
PV как %
цены
облигации ![]()
tPV потока
денег
(1)(4)
(1)
(2)
(3)
(4)
(5)
(6)
1
2
3
4
5
70
70
70
70
1070
0,9524
0,9070
0,8638
0,8227
0,7835
66,668
63,490
60,466
57,589
838,345
6,136%
5,843%
5,565%
5,300%
77,156%
66,668
126,980
181,398
230,356
4191,725
Итого:
1086,558
100%
4797,127
Дюрация D = 4797,127/1086,558 = 4,415 годам. Колонка (5) в этой таблице показывает долю PV каждой ежегодной выплаты в начальной цене облигации, иными словами, величину:
![]()
Но ведь формулу вычисления дюрации можно представить в виде
![]()
Тогда становится понятным определение длительности, как средневзвешенного срока получения всех денежных выплат: каждый срок выплаты (один год - для первой выплаты, два года - для второй и т. д.) умножается на “вес”, равный:
![]()
(сумма этих весов равна 1, или 100%), и затем полученные произведения складываются. Тогда и дюрацию D можно находить, умножая данные столбца (1) на величины столбца (5) и складывая затем полученные результаты:
D = 10,06136+20,05843+30,05565+40,05300+50,77156 = 4,415 годам.
Заметим, что способ вычисления дюрации облигации остается таким же, если купонные выплаты будут осуществляться раз в полгода, или облигация будет иметь какие-то специфические свойства (например, амортизацию долга) – в любом случае время получения каждого денежного потока взвешивается долей этого денежного потока в цене облигации.
При использовании категории дюрации следует учитывать, что с точки зрения процентного риска (т. е. риска воздействия на суммарную отдачу облигации колебаний доходности к погашению) инвестору безразличен выбор между купонной облигацией и бескупонной облигацией, имеющей срок погашения ![]() равный дюрации
равный дюрации ![]() купонной облигации. Использование дюрации предполагает, что реинвестирование всех купонных сумм происходит по неизменной ставке дисконта, равной доходности к погашению
купонной облигации. Использование дюрации предполагает, что реинвестирование всех купонных сумм происходит по неизменной ставке дисконта, равной доходности к погашению ![]() облигации. Однако с учетом рассмотренных выше терминальных зависимостей доходностей, очевидно, что каждая купонная сумма
облигации. Однако с учетом рассмотренных выше терминальных зависимостей доходностей, очевидно, что каждая купонная сумма ![]() должна дисконтироваться по соответствующей спот-ставке
должна дисконтироваться по соответствующей спот-ставке ![]() . Значит, применяя дюрацию, мы должны условно считать, что спот-ставки не меняются. Иными словами, предполагается, что терминальная структура процентной ставки носит горизонтальный характер, и доходности к погашению облигации одинаковы для любого срока погашения.
. Значит, применяя дюрацию, мы должны условно считать, что спот-ставки не меняются. Иными словами, предполагается, что терминальная структура процентной ставки носит горизонтальный характер, и доходности к погашению облигации одинаковы для любого срока погашения.
Свойства дюрации. Дюрация зависит от следующих факторов:
а) доходности к погашению;
б) срока погашения;
в) процента купонных выплат.
Дюрации присущи следующие свойства:
1) Дюрация ![]() бескупонных (чисто дисконтных) облигаций всегда равна сроку их погашения.
бескупонных (чисто дисконтных) облигаций всегда равна сроку их погашения.
2) Дюрация![]() купонных облигаций всегда ниже их срока погашения
купонных облигаций всегда ниже их срока погашения ![]() . При этом, если величина периодических купонных выплат
. При этом, если величина периодических купонных выплат ![]() остается неизменной, то с повышением срока погашения
остается неизменной, то с повышением срока погашения ![]() различие между дюрацией
различие между дюрацией ![]() и сроком погашения
и сроком погашения ![]() возрастает. Например, для облигации с доходностью к погашению
возрастает. Например, для облигации с доходностью к погашению ![]() = 6%, купонной ставкой
= 6%, купонной ставкой ![]() = 8% и сроком погашения
= 8% и сроком погашения ![]() = 5 лет дюрация
= 5 лет дюрация ![]() составляет 4,254 года; если срок погашения облигации возрастает до
составляет 4,254 года; если срок погашения облигации возрастает до ![]() = 20 лет и при этом величины
= 20 лет и при этом величины ![]() и
и ![]() остаются неизменными, то
остаются неизменными, то ![]() = 11,232 лет. В первом случае различие между дюрацией
= 11,232 лет. В первом случае различие между дюрацией ![]() и сроком погашения
и сроком погашения ![]() составляет 0,746 года, а во втором - 9,768 лет. Данное свойство длительности можно объяснить тем, что с увеличением срока
составляет 0,746 года, а во втором - 9,768 лет. Данное свойство длительности можно объяснить тем, что с увеличением срока ![]() доля, приходящаяся на купонные выплаты, возрастет, соответственно доля номинала в суммарном денежном потоке снизится. В этой связи дюрация
доля, приходящаяся на купонные выплаты, возрастет, соответственно доля номинала в суммарном денежном потоке снизится. В этой связи дюрация ![]() , как средневзвешенная величина всех сроков денежных выплат, будет смещаться к середине срока функционирования облигации, увеличивая тем самым различие между дюрацией
, как средневзвешенная величина всех сроков денежных выплат, будет смещаться к середине срока функционирования облигации, увеличивая тем самым различие между дюрацией ![]() и сроком погашения
и сроком погашения ![]() .
.
Как видно из приведенного примера, с увеличением срока ![]() погашения облигации приращение дюрации происходит с затухающим темпом – при
погашения облигации приращение дюрации происходит с затухающим темпом – при ![]() = 5 лет дюрация
= 5 лет дюрация ![]() = 4,254 лет, а при
= 4,254 лет, а при ![]() = 20 лет она составляет лишь 11,232 лет. В этой связи дюрация не может становиться бесконечно большой – своей предельной величины она достигает, если поток будущих доходов не имеет ограничения во времени (например, как уже указывалось, в Великобритании имеются облигации без срока погашения; по ним выплачиваются купонные суммы бесконечно долго). Доказывается, что дюрация не ограниченного во времени потока купонных выплат находится по формуле:
= 20 лет она составляет лишь 11,232 лет. В этой связи дюрация не может становиться бесконечно большой – своей предельной величины она достигает, если поток будущих доходов не имеет ограничения во времени (например, как уже указывалось, в Великобритании имеются облигации без срока погашения; по ним выплачиваются купонные суммы бесконечно долго). Доказывается, что дюрация не ограниченного во времени потока купонных выплат находится по формуле:
 , где
, где ![]() - ставка дисконта.
- ставка дисконта.
Отметим также, что если облигация продается по номиналу или выше номинала, то с повышением срока погашения ![]() дюрация облигации постоянно возрастает (с затухающим темпом). Если же облигации реализуются с дисконтом (ниже номинала), то с увеличением срока
дюрация облигации постоянно возрастает (с затухающим темпом). Если же облигации реализуются с дисконтом (ниже номинала), то с увеличением срока ![]() дюрация облигации сначала также возрастает, но затем может снижаться. Как установлено (доказательство этому опущено), если по облигации выплачиваются купонные суммы
дюрация облигации сначала также возрастает, но затем может снижаться. Как установлено (доказательство этому опущено), если по облигации выплачиваются купонные суммы ![]() , срок ее погашения
, срок ее погашения ![]() лет, а доходность к погашению
лет, а доходность к погашению ![]() %, то дюрация облигации находится по формуле:
%, то дюрация облигации находится по формуле:
![]()
Если облигация продается с дисконтом, то у нее ![]() <
< ![]() . Тогда при относительно высоких значениях
. Тогда при относительно высоких значениях ![]() числитель второго слагаемого:
числитель второго слагаемого: ![]() может стать отрицательным, и дюрация облигации начнет понижаться по мере роста срока погашения. Это свойство отчетливо проявляется при значительных дисконтах. Например, если у облигации купонная ставка
может стать отрицательным, и дюрация облигации начнет понижаться по мере роста срока погашения. Это свойство отчетливо проявляется при значительных дисконтах. Например, если у облигации купонная ставка ![]() =6%, а доходность к погашению
=6%, а доходность к погашению ![]() = 16%, то когда срок погашения облигации превысит 11,6 лет, числитель второго слагаемого станет отрицательным, и дюрация облигации по мере увеличения срока погашения начнет уменьшаться.
= 16%, то когда срок погашения облигации превысит 11,6 лет, числитель второго слагаемого станет отрицательным, и дюрация облигации по мере увеличения срока погашения начнет уменьшаться.
3) Как правило, для одного и того же срока погашения ![]() дюрация
дюрация ![]() облигации будет тем ниже, чем выше величина купонных выплат (и наоборот). Например, для рассмотренной нами облигации (
облигации будет тем ниже, чем выше величина купонных выплат (и наоборот). Например, для рассмотренной нами облигации (![]() =5 лет;
=5 лет; ![]() =5%;
=5%; ![]() =7%;
=7%; ![]() = 4,415 лет) при увеличении величины купонных выплат до 9% дюрация сократится до 4,296 лет, а если купонные выплаты снизятся до 5%, то
= 4,415 лет) при увеличении величины купонных выплат до 9% дюрация сократится до 4,296 лет, а если купонные выплаты снизятся до 5%, то ![]() повысится до 4,546 лет. Это свойство также можно объяснить тем фактом, что повышение купонных ставок увеличивает долю купонных выплат в общем потоке денежных средств от облигации, смещая тем самым средневзвешенную величину сроков денежных выплат к середине срока действия облигации. Необходимо также заметить, что это свойство может нарушаться для случаев высоких значений доходности к погашению
повысится до 4,546 лет. Это свойство также можно объяснить тем фактом, что повышение купонных ставок увеличивает долю купонных выплат в общем потоке денежных средств от облигации, смещая тем самым средневзвешенную величину сроков денежных выплат к середине срока действия облигации. Необходимо также заметить, что это свойство может нарушаться для случаев высоких значений доходности к погашению ![]() (когда облигации продаются с большим дисконтом) и значительным сроком до погашения (о чем говорилось выше).
(когда облигации продаются с большим дисконтом) и значительным сроком до погашения (о чем говорилось выше).
4) При неизменных величинах купонных выплат ![]() и срока погашения
и срока погашения ![]() , чем ниже величина доходности к погашению
, чем ниже величина доходности к погашению ![]() , тем выше значение дюрации
, тем выше значение дюрации ![]() . Это свойство объясняется тем фактом, что снижение ставки дисконта приводит к нелинейному росту факторов дисконта. Поэтому, чем более отдален во времени срок платежа, тем относительно на большую сумму он возрастает при снижении ставки дисконта. В результате относительная доля номинала в суммарном потоке доходов будет повышаться, увеличивая тем самым дюрацию
. Это свойство объясняется тем фактом, что снижение ставки дисконта приводит к нелинейному росту факторов дисконта. Поэтому, чем более отдален во времени срок платежа, тем относительно на большую сумму он возрастает при снижении ставки дисконта. В результате относительная доля номинала в суммарном потоке доходов будет повышаться, увеличивая тем самым дюрацию ![]() облигации
облигации
Следует отметить, что использованные до этого формулы (9.22) и (9.22а) применяются в том случае, если облигация приобретается в день купонных выплат. Если дата покупки облигации не совпадает с днем купонной выплаты, то дюрацию облигации определяют по более сложной формуле:
![]() (4.3)
(4.3)
4.3. Использование дюрации для оценки риска облигаций.
Категория дюрации ![]() используется в оценке волатильности цены облигации. В основу таких оценок можно положить тот факт, что дюрация облигации представляет собой эластичность цены облигации
используется в оценке волатильности цены облигации. В основу таких оценок можно положить тот факт, что дюрация облигации представляет собой эластичность цены облигации ![]() по фактору дисконта
по фактору дисконта 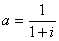 . Действительно, по определению, цена облигации определяется по формуле:
. Действительно, по определению, цена облигации определяется по формуле:
![]() , где
, где 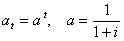
По общему определению, эластичность e величины ![]() по фактору дисконта
по фактору дисконта 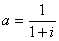 (то есть дюрация
(то есть дюрация ![]() ) должна находиться из выражения:
) должна находиться из выражения:
![]()
Поскольку эластичность показывает, на сколько процентов изменится функция при изменении аргумента на 1%, то дюрация также должна показывать, на сколько процентов изменится цена облигации![]() (функция) при изменении фактора дисконта
(функция) при изменении фактора дисконта ![]() (аргумента) на 1%. Однако, как указывалось выше, фактор дисконта и ставка дисконта связаны нелинейной зависимостью, поэтому при оценке волатильности облигации, то есть степени реакции ее цены на изменения доходности к погашению, используют линейную зависимость
(аргумента) на 1%. Однако, как указывалось выше, фактор дисконта и ставка дисконта связаны нелинейной зависимостью, поэтому при оценке волатильности облигации, то есть степени реакции ее цены на изменения доходности к погашению, используют линейную зависимость ![]() и
и ![]() . Тогда связь между изменениями доходности к погашению
. Тогда связь между изменениями доходности к погашению ![]() облигации и изменениями ее цены
облигации и изменениями ее цены ![]() можно представить в виде следующего равенства:
можно представить в виде следующего равенства:
процентное изменение ![]() =
=![]()
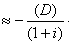 (% изменения ) (4.4)
(% изменения ) (4.4)
Величину ![]() принято называть модифицированной дюрацией (МD). Тогда:
принято называть модифицированной дюрацией (МD). Тогда:
процентное изменение - МD(% изменения ![]() ) (4.5)
) (4.5)
В данной формуле знак “минус” свидетельствует, что изменения величин ![]() и
и ![]() происходит в обратном направлении.
происходит в обратном направлении.
Метод использования модифицированной дюрации МD для оценки процентного изменения цены облигаций при колебаниях рыночной процентной ставки (что найдет отражение в изменениях доходности к погашению) дает более точные результаты в случае его применения для относительно краткосрочных облигаций с высокими ставками купонных выплат, чем для долгосрочных облигаций с низкими купонными выплатами.
Волатильность облигации можно определить следующим образом:
волатильность = 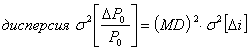
Поэтому, если имеют одинаковые доходности к погашению, но различные дюрации, то их волатильность может отличаться.
Тема 5
Формирование и управление портфелем облигаций.
Важным преимуществом инвестирования в облигации является то, что при формировании и управлении портфелем облигаций инвестор может преследовать различные стратегические цели, в частности:
1) добиться потока стабильного дохода, получаемого через определенные промежутки времени;
2) аккумулировать запланированную сумму денег к определенной дате;
3) повысить отдачу портфеля либо за счет удачного прогноза движения процентной ставки, либо путем получения прибыли за счет изменения соотношения цен и доходности к погашению облигации.
Рассмотрим эти инвестиционные стратегии подробно.
5.1. Формирование и управление портфелем с целью получения потока стабильного дохода.
Облигации служат удобным средством для тех инвесторов, которые желают обеспечить себе стабильный поток относительно высокого дохода за счет регулярных купонных выплат и получения начальной стоимости (номинала) облигации при ее погашении. Наиболее удачным способом достижения этой цели служит простая покупка надежных (в смысле кредитного риска) и относительно высокодоходных облигаций и сохранение их вплоть до погашения (или до окончания более короткого запланированного инвестором срока). Имея поставленную цель - получать желаемый годовой доход – инвестор должен скомпоновать в портфеле такое количество облигаций, чтобы их суммарные купонные выплаты равнялись необходимому доходу.
Предположим, что инвестор располагает 5000 руб. и желает 1 января 2009 года сформировать портфель облигаций с постоянным высоким доходом. Для простоты будем полагать, что номинал всех облигаций равен 1000 руб. Тогда, выбрав облигации с максимальной текущей доходностью к погашению при допустимом уровне надежности (кредитного риска), инвестор должен сформировать приблизительно следующий портфель:
Таблица 9.
Пример формирования портфеля облигаций
Вид облигации
(эмитент)
Номинал
(руб.)
Текущая
цена (руб.)
Текущая
YTM (%)
Ставка купонных
выплат (%)
Годовой
доход (руб.)
Срок
погашения![]()
Облигация
фирмы А
Облигация
концерна В
Облигация
корпорации С
Государственная.
облигация D
Облигация
объединения Е
1000,00
1000,00
1000,00
1000,00
1000,00
998,13
1001,79
996,63
1003,74
1003,97
9,5
9,1
9,0
9,15
8,9
9,3
9,2
8,9
9,25
9,00
93
92
89
92,5
90
1.01.2010
1.01.2011
1.01.2012
1.01.2013
1.01.2021
Итого:
5000,00
5004,26
456,5
*) совпадающие даты погашения выбраны в целях упрощения расчетов
Как видно из таблицы, суммарная рыночная цена облигаций (5004 руб.) не на много превосходит ресурсы инвестора. Данный портфель принесет инвестору через год доход в размере 1456,5 руб. (1000 руб. он получит при погашении облигации А плюс сумма купонных выплат). Доход от номинала он должен потратить на покупку очередной облигации F, срок погашения которой наступит, положим, 1 января 2014 года. То же он должен сделать 1 января 2011 года, купив облигацию со сроком погашения в 2015 году и т. д., чтобы иметь возможность каждый год получать доход от номинала и тратить его на приобретение очередной облигации.
Конечно, колебания рыночной ставки процента могут понизить отдачу портфеля в какой-то момент, но, увеличив число облигаций в портфеле и растянув во времени процесс его обновления, инвестор способен сгладить отрицательные последствия падения процентных ставок, так как в длительных периодах отклонения процентной ставки в обе стороны уравновешивают друг друга.
Следует заметить, что достоинство подобного портфеля - это отсутствие необходимости его постоянного управления, поскольку купонные суммы не реинвестируются и облигации не реализуются раньше срока их погашения. Фактически инвестор проводит корректировку портфеля раз в год, когда решает какую облигацию приобрести взамен погашенной. Однако главный недостаток такого портфеля состоит в том, что он не позволяет раскрыть все потенциальные возможности отдачи облигаций.
Эта стратегия несет определенный риск, вызываемый рядом обстоятельств. Во-первых, удерживая облигации вплоть до их погашения, инвестор избегает ценового риска (риска ликвидности), но одновременно значительно повышается кредитный риск, связанный с возможностью несоблюдения обязательств эмитентом. Во-вторых, желание обеспечить максимальный доход будет подталкивать инвестора на приобретение высокодоходных облигаций, которые имеют, как правило, и меньшую надежность. В-третьих, инвестор должен сформировать портфель таким образом, чтобы ежегодно в нем заменялась новыми облигациями после погашения старых небольшая часть ценных бумаг, то есть процесс погашения облигаций шел последовательно, невысокими порциями. Если инвестор так подберет облигации, что в какой-то момент будет гаситься значительная часть портфеля, то время замены может совпасть с периодом низкого уровня рыночной процентной ставки, в результате чего инвестор вынужден будет реинвестировать купонные суммы по более низким ставкам, и его доход снизится.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 |





