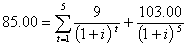
Воспользовавшись компьютером или приближенным методом вычисления, можно вычислить искомую величину . Заметим, что и в этом случае доходность к моменту отзыва предполагает реинвестирование всех купонных сумм вплоть до момента отзыва по ставке процента, равной доходности к моменту отзыва.

3.2. Основные составляющие отдачи облигаций.

Отдача любой ценной бумаги за холдинговый период определяется по формуле:

PT+1 + D - PT

rT+1 = ¾¾¾¾¾¾¾¾

PT

где: rT+1 - отдача финансового средства в конце холдингового периода;

PT+1 - цена финансового средства в конце холдингового периода;

D - дополнительный доход (дивиденд по акции, процент по облигации), получаемый за холдинговый период;

PT - цена финансового средства в начале холдингового периода.

Данная формула применима для любого финансового средства и широко используется в частности в теории инвестиционного портфеля. Однако она показывает отдачу только тех ценных бумаг, которые приносят доход один раз за холдинговый период. Между тем, многие инвесторы вкладывают деньги в такие финансовые средства, как, например, облигации, приносящие регулярные доходы несколько раз за холдинговый период. В этой связи их интересуют способы подсчета средней годовой доходности, которую можно использовать для определения отдачи инвестиций за долгосрочный период.

Такая годовая доходность должна учитывать возможность получения сложного процента, то есть реинвестирование купонных выплат. Именно этим обстоятельством многопериодная доходность отличается от однопериодной доходности. В многопериодном варианте отдача облигации может содержать три составляющие:

1) Цена отчуждения облигации. Чаще эта цена может быть задана как:

а) номинал облигации - если облигация сохраняется инвестором до погашения;

б) цена продажи - если инвестор продает облигацию ранее срока ее погашения;

в) цена отзыва в случае наличия такой возможности

2) Сумма купонных выплат.

3) Процент на процент

Следует иметь в виду, что недоучет последней составляющей может серьезно исказить результаты оценки средней геометрической ежегодной доходности. Во всяком случае, необходимо помнить, что обещанная (предполагаемая) многопериодная доходность (годовая средняя геометрическая), измеренная как доходность к погашению , однозначно предполагает реинвестирование купонных выплат по ставке процента, равной величине доходности к погашению , чтобы заработать эту доходность. Иначе говоря, доходность к погашению - это прогнозируемая величина, и она показывает предполагаемую (ожидаемую) среднюю геометрическую ежегодную доходность за холдинговый период с многократными выплатами. Реальная же средняя геометрическая ежегодная доходность подсчитывается на основании уже наблюдавшихся результатов и может совпадать с предполагаемой доходностью только при определенных условиях.

Итак, для определения многопериодной доходности инвестор обязан учитывать третью составляющую своего потенциального дохода - сложный процент на купонные выплаты. Но столь ли существенна эта составляющая, чтобы ей нельзя было пренебречь? Проведем оценку: предположим, что инвестор приобретает облигацию со сроком погашения 30 лет по номинальной стоимости и ежегодной купонной ставкой 8%. Если облигация приобретена по номиналу, то ее доходность к погашению, а следовательно и прогнозируемая годовая средняя геометрическая доходность, равна купонной ставке и составляет 8%. Пусть в последующие 30 лет инвестор реинвестирует все полученные купонные суммы по ставке 8%. Тогда через 30 лет его суммарный доход составит:

1000´(1,08)30 = 10062,7 руб.

и годовая средняя геометрическая ставка будет равна величине:

(10062,7/1000)1/30 -1=0,08 или 8%.

Из чего же состоит суммарный доход инвестора? Во-первых, это выплаченная в момент погашения номинальная стоимость облигации 1000 руб. Во-вторых, за 30 лет он 30 раз получит купонные выплаты, то есть суммарные процентные выплаты равны: 30´80=2400 руб. Итого, две первые составляющие дают в общей сложности: 1000 + 2400 = =3400 руб., а остальные 6662,7 руб. обеспечивает третья составляющая отдачи облигации - процент на процент. Значит, из общей величины полученного инвестором дохода в 10062,7 руб., сумма в 6662,7 руб., или (6662,7/10062,7)= =0,662, то есть 66,2%, составляет процент на процент.

К определению суммы процента на процент можно подойти и другим образом. Если предполагается, что инвестор реинвестирует каждую купонную сумму по ставке процента, равной доходности к погашению , то полученную через год первую купонную сумму можно реинвестировать ее по ставке = 7% на оставшиеся до погашения 29 лет. К моменту погашения эта первая купонная сумма обеспечит доход 70 руб.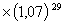. Соответственно, реинвестирование второй купонной суммы на оставшиеся до погашения 28 лет даст к моменту погашения доход 70 руб. 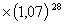и т. д. В итоге реинвестирование всех купонных сумм обеспечит к моменту погашения доход, определяемый будущей стоимостью FV купонных сумм :

FV =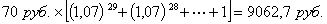

Для вычисления будущей стоимости FV купонных сумм , реинвестируемых по ставке процента в течение n шагов расчета, можно использовать следующую формулу:

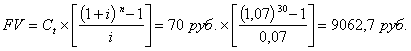
Однако из этой суммы 2400 руб. приходятся на тридцать купонных выплат, а оставшиеся 6662,7 руб. и составляют процент на процент.

Но для получения такого дохода, а, следовательно, и предполагаемой доходности (или, что равноценно, доходности к погашению) инвестор должен реинвестировать купонные суммы по ставке процента, равной доходности к погашению.

А что произойдет, если инвестор не будет реинвестировать купонные выплаты? В таком случае его суммарный доход через 30 лет будет содержать только две компоненты - номинал и суммарные купонные выплаты, то есть составит всего: 1000+2400=3400 руб., а реализованная средняя геометрическая годовая доходность будет равна: (3400/1000)1/30 - 1=0,042 или 4,2%, то есть почти в два раза ниже предполагаемой доходности к погашению.

Поскольку третья компонента суммарной отдачи облигации предполагает начисление сложного процента на купонные выплаты, то, очевидно, что эта компонента будет зависеть в основном от двух факторов - величины купонной выплаты и срока до момента погашения: с ростом величины купонной ставки и срока до погашения доля процента на процент в суммарном доходе повышается.

3.3. Измерение суммарной отдачи в случае продажи облигации до срока погашения.

Рассмотренные выше примеры вычисления составляющих отдачи облигаций предполагали, что инвестор держит облигации вплоть до их погашения. Однако на практике многие инвесторы продают эти ценные бумаги раньше срока погашения. Методика определения суммарной отдачи облигации в случае ее досрочной продажи содержит ряд особенностей, поскольку предполагает вычисление трех составляющих уже по отношению ко дню продажи, а не к моменту погашения. Кроме того, вместо номинальной стоимости облигации (которую получают при ее погашении) необходимо брать цену продажи облигации. Если мы сегодня хотели бы определить составляющие дохода облигации в будущем (к моменту ее продажи), то главная сложность состоит в определении предполагаемой стоимости облигации в день ее реализации. Данная операция подразумевает прогнозирование рыночной ставки процента, по которой необходимо будет дисконтировать потоки денег, оставшиеся не реализованными к моменту продажи облигации. В случае определения отдачи в момент продажи облигации, необходимо пользоваться уже наблюдающимися, реализованными (а не прогнозируемыми) данными о цене продажи.

Пример 7: предположим, что инвестор покупает по номинальной стоимости облигацию со сроком погашения 10 лет и купонными выплатами = 7%, выплачиваемыми ежегодно (если облигация приобретена по номинальной стоимости, то в момент продажи ее доходность к погашению также составляла 7%). При этом инвестор уверен, что ему удастся реинвестировать получаемые купонные выплаты по ставке 8% в течение 7 лет, после чего он намерен продать облигацию. Из каких составляющих формируется его суммарный доход в момент продажи облигации и чему будет равна доходность к моменту продажи, или средняя годовая геометрическая доходность облигации?

Во-первых, определим предполагаемую цену продажи облигации, то есть приведенную стоимость оставшихся потоков денег. До погашения облигации через 7 лет останется 3 года; в каждый из этих лет инвестор должен получать купонные выплаты, а в момент погашения ему выплатят номинал. Ставка дисконта i = 8%. Отсюда цена продажи:

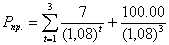= 97.38

Остальные составляющие отдачи облигации находим, исходя из того, что реинвестирование 70 руб. по ставке 8% в течение 7 лет даст в общей сложности 624,6 руб. = 70×(1,08) + 70×(1,08)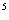+ 70×(1,08)+…+70 руб. Из этого дохода сумму 70´7 = 490 руб. составят суммарные купонные выплаты, а (624,=134,6 руб. составят проценты на процент.

Итак, суммарная отдача облигации через 7 лет в момент ее продажи будет содержать три части:

1) цена продажи - 973,8 руб.

2) суммарные купонные выплаты - 490 руб.

3) проценты на процент - 134,6 руб.

то есть в общей сложности: 973,8+490+134,6=1598,4 руб. Ожидаемая средняя геометрическая годовая доходность составит: (1598,4/1000)1/7 - 1=0,0693 или 6,93%.

В заключение еще раз обратим внимание на важность категории доходности к погашению для инвесторов, вкладывающих деньги в облигации. Во-первых, доходность к погашению показывает ту ставку процента, которую необходимо использовать при дисконтировании денежных потоков для определения цены облигации. Во-вторых, доходность к погашению показывает прогнозируемую (ожидаемую, обещанную) многопериодную среднюю геометрическую доходность, которую инвестор ожидает получить от облигации в случае реинвестирования купонных сумм по ставке процента, равной доходности к погашению.

3.4. Факторы, определяющие доходность облигации.

Доходность к погашению каждой облигации аналогично любой процентной ставке может быть представлена суммой безрисковой ставки процента и премии за риск :

.

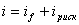Одновременно, как отмечалось ранее, безрисковая ставка процента является номинальной величиной и для невысоких темпов инфляции может быть представлена в виде суммы реальной ставки процента  и уровня инфляции :

.

Следовательно, в общем случае доходность к погашению является комбинацией трех составляющих:

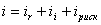(3.9)

Реальная ставка процента и уровень инфляции определяются  макроэкономическими факторами и являются общими для всех облигаций. А вот фактором, отличающим доходность одной облигации от другой, служит надбавка за риск.

Вознаграждение за риск  является третьей и наиболее важной компонентой отдачи облигации, отличающей доходность одной облигации от доходности другой. Можно отметить многие факторы, влияющие на риск, связанный с приобретением облигации. К наиболее важным из них можно отнести:

1) возможность банкротства фирмы-эмитента;

2) ликвидность облигации;

3) существование каких-либо условий выпуска облигаций;

4) срок погашения облигации.

Если доход с облигации облагается налогом, то необходимо учитывать и эту компоненту риска. Остановимся подробнее на составляющих риска облигации.

1) Риск банкротства эмитента (кредитный риск). Надбавка за этот риск компенсирует инвестору возможность неполучения положенных денег в случае невозможности заемщика выполнить взятые обязательства. Как правило, инвесторы в своей оценке кредитного риска облигаций пользуются услугами специализированных рейтинговых компаний, проводящих ранжирование выпущенных облигаций. При этом исследователи изучают сферу деятельности эмитента и его потребности, положение фирмы в отрасли, ее общее финансовое состояние (возможность выплатить проценты и номинал, ликвидность и прибыльность ее средств, кредитоспособность). Чем выше ранг (рейтинг) облигации, тем меньше ее кредитный риск.

Наиболее крупными рейтинговыми агентствами являются две американские компании Moody's Investors Service (Moody's) и Standard & Poor's Corporation (S&P). Ниже в таблице 2 приводится содержание рейтингов этих агентств.

Следует иметь в виду, что ранжируются облигации, а не фирмы-эмитенты. Одна и та же фирма может выпустить две облигации разного ранга - например, одна облигация может быть обеспечена залогом, и ее ранг будет выше необеспеченной залогом облигации. Кроме того, ранг облигации может измениться в виду перемен в финансовом статусе фирмы - ее серьезные финансовые сложности могут подорвать доверие к облигациям и вызвать снижение их рейтинга.

Таблица 2.

Рейтинги облигаций

S&P

Соответствующий

рейтинг Moody's

Облигации с инвестиционным рейтингом

AAA

Облигации с данным рейтингом имеют высшую степень надежности с точки зрения выплаты эмитентом купонных сумм и номинала

Aaa

AA+

AA

AA-

Облигации с рейтингом АА имеют очень высокую способность обеспечивать купонные выплаты и номинал. Обладают чуть меньшей надежностью, чем облигации с рейтингом ААА

Aa1

Aa2

Aa3

А+

А

А-

Данные облигации обеспечивают также высокую способность эмитента выплачивать купонные суммы и номинал, хотя они в более высокой степени подвержены воздействию изменений экономической ситуации, чем облигации высшего рейтинга

А1

А2

А3

ВВВ+

ВВВ

ВВВ-

Данные облигации обеспечивают достаточно высокую способность эмитента производить положенные выплаты. Хотя часто они имеют определенное обеспечение, негативные события на рынке могут значительно снизить возможности эмитента исполнять свои обязательства

Ваа1

Ваа2

Ваа3

Спекулятивные облигации / Низкий уровень кредитоспособности эмитента

ВВ+

ВВ

ВВ-

В+

В

В-

ССС+

ССС

ССС-

СС+

СС

СС-

Данные облигации относятся к преимущественно спекулятивным видам. Способность эмитента выплачивать купонные суммы и номинал определяются условиями взятых обязательств. Хотя зачастую эти облигации имеют то или иное обеспечение, высокая степень неопределенности и обусловленный этим риск снижают уровень предоставленных гарантий

Ва1

Ва2

Ва3

В1

В2

В3

Саа

Са

Преимущественно спекулятивные / Значительные риск или дефолт

С

Данный рейтинг присваивается т. н. доходным облигациям, купонные выплаты по которым осуществляются лишь в том случае, когда прибыль эмитента достигла установленного уровня

C

D

Эмитент объявил о своем дефолте

Рейтинги облигаций играют большую роль в инвестиционной деятельности. Например, институциональные инвесторы (пенсионные фонды, страховые компании, коммерческие банки и др.) во многих странах не имеют права вкладывать средства в облигации с низким рейтингом. Кроме того, надо учитывать, что от рейтинга облигации напрямую зависит стоимость заимствования эмитентом необходимых средств – чем ниже рейтинг, тем более высокую цену (в виде купонных сумм или дисконта) должен заплатить эмитент. Так, в разные промежутки времени стоимость заимствования по облигациям с рейтингом ААА на 25-40 процентных пунктов (0,25% - 0,40%) ниже, чем по облигациям рейтинга АА. Различие же с облигациями рейтинга В могут достигать 9% и более.

2) Риск ликвидности. Инвестор должен получать компенсацию за риск облигации, связанный с невозможностью ее быстрой продажи по адекватной цене. Таким риском обладают многие облигации местных органов власти

3) Риск существования каких-либо условий выпуска облигаций. Отдельные выпуски облигаций содержат заранее оговоренные условия, например, возможность отзыва облигации в случае значительного снижения их доходности. Такие условия также требуют соответствующей компенсации инвестору за риск: право отзыва делает неопределенным будущие потоки денег. Кроме того, инвестор понимает, что снижение доходности облигации происходит обычно в условиях общего снижения ставок процента, поэтому реинвестировать купонные суммы ему придется по более низким ставкам - он также потребует компенсации и за это.

4) Риск срока погашения облигации. Доходность облигации зависти от срока, оставшегося до ее погашения. Если называть оставшийся до погашения облигации срок терминальным, то в каждый момент времени  мы можем определить терминальную структуру  доходности облигации, которая представляет зависимость между доходностью и сроком, оставшимся до погашения облигации. Важно только при этом иметь в виду, что для раскрытия терминальной структуры мы должны рассматривать данную зависимость при прочих равных условиях, то есть, полагая, что исследуемые облигации имеют все факторы, кроме срока погашения, абсолютно одинаковыми (и кредитный риск, и риск ликвидности, и купонные выплаты, и пр.). Лучше всего для этих целей подходят государственные бескупонные облигации (они лишены кредитного риска, не имеют купонных выплат, практически одинаково ликвидные).

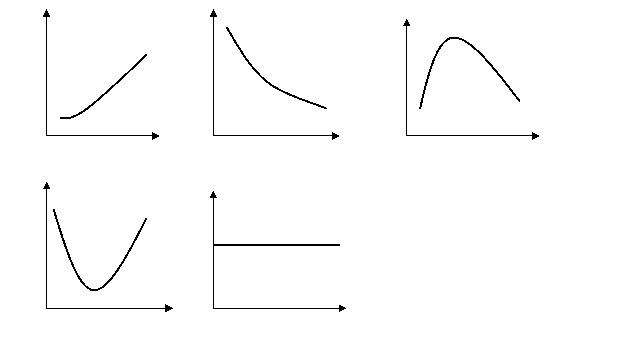
а) б) в)

г) д)

 Рисунок 2. Типы терминальной структуры доходности к погашению

На рисунке по вертикальной оси отложены значения доходности к погашению (YTM), а по горизонтальной - годы, оставшиеся до погашения облигаций.

Многочисленные эмпирические построения терминальной структуры доходности облигаций свидетельствуют об отсутствии какой-либо единой теоретической зависимости между доходностью к погашению облигаций и сроком их погашения. В разные периоды времени эта зависимость может быть совершенно различной. Наглядно это показано на рисунке 2, где приведены различные типы зависимости YTM и срока до погашения облигации.

В настоящее время известны три основные теоретические модели возможного объяснения терминальной структуры доходности облигаций:

1) инвестиционных ожиданий будущих ставок процента;

2) ликвидной премии;

3) рыночной сегментации.

Все они основаны на использовании двух новых понятий: спот-ставки процента и форвардной ставки процента. Под  спот ставкой понимают доходность к погашению чисто дисконтной облигации в данный момент времени, и в этом смысле она может ассоциироваться со ставкой процента, устанавливаемой при заключении спот контрактов. Такие контракты предполагают немедленное предоставление займа одной стороной другой стороне в момент подписания контракта и выплату занятой суммы с процентом в строго оговоренный срок.

Обратимся к рассмотренным ранее облигациям A, B,C. Облигации A и B являются чисто дисконтными, бескупонными, поэтому их доходности к погашению (вычисленные в рассматриваемый нами момент времени) определяют и спот ставки - одногодичную = 7,5% и двухгодичную = 8,5% соответственно. Следовательно, если бы в рассматриваемый момент времени инвестор заключал спот-контракт и хотел бы через год получить от заемщика 1000 руб., то он должен дать ему взаймы сумму, равную:

1000/(1,075)=930,2 руб.

Если бы спот-контракт заключался на два года, то инвестору надо дать в долг заемщику:

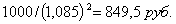
чтобы через два года получить возврат долга плюс процент (всего 1000 рублей).

Однако может сложиться ситуация, что в момент заключения двухгодичного спот-контракта на рынке отсутствуют государственные бескупонные облигации с двухлетним сроком погашения. В этом случае двухлетнюю спот-ставку вычисляют по купонной облигации, используя текущую цену  купонной облигации, ее купонную выплату  через один год и выплату (  + ) в момент погашения, а также одногодичную спот-ставку :

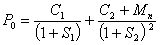
где  - предполагаемая двухлетняя спот-ставка. Например, если считать, что на рынке существуют только облигации A и C, то двухлетнюю спот-ставку  в рассматриваемый период надо находить из равенства:

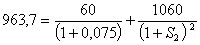
Решение дает величину  = 8,053%.

Форвардная ставка. Вернемся к двухлетней спот-ставке. Как мы показали, в случае заключения двухлетнего спот-контракта инвестор даст в долг 849,5 руб. под двухлетнюю спот-ставку  = 8,5% и через два года получит сумму:

.

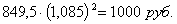Однако схему предоставления займа можно несколько видоизменить, оставив теми же начальную и конечную сумму контракта. Представим, что начисление процента на первоначальную сумму идет в два этапа: в первый год она равна однолетней спот-ставке , а на следующий (второй) год определяется как  ожидаемая  однолетняя спот-ставка , которая, как предполагается, установится на рынке в конце первого года. Иными словами, в конце первого года сумма долга заемщика возрастет до величины: (1+ )×849,5 руб., а в конце второго года – до величины: (1+ )×(1+ )×849,5 руб. По условию, эта сумма должна составить 1000 руб. Отсюда мы можем вычислить ставку :

(1,075)×(1+ )×849,5 = 1000 руб. (9.15)

откуда   = 0,0951 или 9,51%.

Контракты, при которых в момент их заключения суммы будущих процентных выплат определяются прогнозируемыми, ожидаемыми ставками процента через какой-то промежуток времени, называются форвардными, а используемая ставка процента - форвардной (в нашем случае - от года один к году два).

Выражение (9.15) можно записать в ином виде:

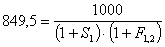
и рассматривать его как равенство для вычисления приведенной стоимости будущего потока денег. В таком случае форвардная ставка  может быть определена как ставка дисконта для вычисления той суммы, которую необходимо инвестировать через год после подписания контракта, и которая должна составить приведенную стоимость PV1 дохода, ожидаемого через два года:

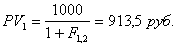
В свою очередь, спот-ставка  - это ставка дисконта, приравнивающая приведенную стоимость величины PV1 к 849,5 руб., то есть:

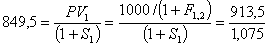
Очевидно, что в нашем случае:

Следовательно, зная две спот-ставки и  , мы в состоянии вычислить форвардную ставку .

Перейдем теперь к рассмотрению теорий, в которых делается попытка объяснить терминальную структуру доходности к погашению облигаций.

Теория ожиданий будущей ставки процента  основывается на следующем предположении: существует общее мнение инвесторов о том, что форвардные ставки представляют собой ожидаемые спот-ставки в будущем. В этой связи возрастание спот-ставок (восходящая кривая терминальной зависимости) может объясняться тем, что в данный момент инвесторы ожидают рост однолетних спот-ставок в будущем (поскольку мы рассматриваем безрисковые ценные бумаги, то ожидание повышения будущих спот-ставок может объясняться изменениями реальной ставки процента или уровня инфляции).

Теория ожиданий процентной ставки в чистом виде предполагает, что инвесторы нейтральны к риску и приобретают ценные бумаги, которые обеспечивают им наивысшую отдачу вне зависимости от длительности инвестиционного горизонта. Именно поэтому она подходит для объяснения любого вида кривой терминальной зависимости процентных ставок. Следует при этом учитывать, что данная теория предполагает ряд допущений:

- инвесторы имеют гомогенные ожидания;

- инвесторы осуществляют выбор между краткосрочными и долгосрочными облигациями на основе критерия максимизации ожидаемого дохода за время инвестирования;

- не учитываются транзакционные издержки;

- рынок облигаций эффективен, то есть новая информация немедленно трансформируется в изменения цен облигаций.

Теория ликвидной премии. Согласно теории ожиданий процентных ставок, инвестору безразлично, какую из трех альтернатив выбрать - покупать ли сразу, положим, 5-ти летнюю ценную бумагу, или последовательно приобретать пять годичных облигаций, или, наконец, купить облигацию со сроком погашения 8 лет и продать ее через 10 лет. Однако, в реальной действительности инвесторы предпочтут вкладывать деньги в последовательную череду однолетних облигаций, чем в долгосрочные. Представим, что инвестор купил 10-летнюю облигацию, и через 4 года возникла необходимость продать ее (инвестору срочно понадобились деньги). Если к моменту продажи доходность к погашению облигации повысится, то ее цена упадет, и инвестор сможет продать облигацию только по цене ниже

номинала.

Значит, обладание долголетней государственной облигацией (теоретически не имеющей риска дефолта) несет в себе риск, связанный с неопределенностью ее будущей цены в случае необходимости продажи (ликвидации) облигации до срока погашения. Этот риск называют  ценовым (price risk), или риском ликвидности (liquidity risk). В таком случае, дополнительный риск должен быть дополнительно оплачен. Иначе говоря, пятилетняя спот-ставка должна превосходить среднюю геометрическую годовую ставку пяти последовательно купленных одногодичных облигаций.

Как следует из теории ликвидной премии, инвесторы предпочитают ликвидные ценные бумаги. Поскольку долгосрочные облигации отличаются меньшей ликвидностью, то инвесторы снижают спрос на такие бумаги, и увеличивают вложения в краткосрочные активы. В этой связи теория ликвидной премии в основном объясняет восходящий тип кривых терминальной структуры.

Теория рыночных сегментов исходит из предположения, что существует сегментация финансового рынка. Многочисленные инвесторы и заемщики, как предполагается, исходя из различных законодательных положений, своих предпочтений или традиций, выбирают различные сроки погашения облигаций. В этой связи существует рынок краткосрочных, рынок среднесрочных и рынок долгосрочных обязательств. Согласно данной теории, спот-ставки определяются взаимодействием спроса и предложения на каждом сегменте рынка. Восходящий тип терминальной структуры объясняется тем, что на рынке долгосрочных облигаций взаимодействие спроса на эти ценные бумаги и их предложения обеспечивает более высокую ставку процента, чем на рынке краткосрочных обязательств. При обратной картине кривая будет иметь падающий характер.

Теория рыночной сегментации удобна для объяснения терминальной структуры в долгосрочных периодах. Согласно этой теории, в рамках определенного диапазона доходности к погашению спрос и предложение денег определяют соответствующую цену облигации. Если теория рыночной сегментации подтверждается, то и в ней ожидаемые спот-ставки меньше форвардных ставок на величину премии. Эта теория критикуется в основном на том основании, что если инвесторы имеют четкие предпочтения с точки зрения срока погашения облигаций, эффект сегментации рынка нивелируется как только отдельные инвесторы начнут оценивать относительные доходности и распределять свои средства в другие сегменты, где облигации обеспечивают относительно более высокую доходность. Конечно, любой инвестор стремится снизить риск инвестирования, оставаясь в предпочитаемом им сегменте рынка, но он будет переходить в другие сегменты, как только премия за риск будет достаточной, чтобы перекрыть предполагаемый риск инвестирования и потери от перехода в другой сегмент.

Обратим внимание на важный факт: терминальная структура процентных ставок основана на использовании спот-ставок, т. е. на доходности бескупонных облигаций. Она отражает соотношение спот-ставок и соответствующих дат погашения бескупонных облигаций. Так как такие облигации не всегда имеются для каждой даты погашения и поскольку публикуются данные по спот-ставкам только государственных облигаций, большинство инвесторов используют т. н. кривые доходности. Они показывают соотношения доходностей к погашению и соответствующих дат погашения различных, в том числе и купонных, облигаций. Они публикуются в периодической печати, доступны для пользователей Интернета.

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6