Поскольку купонные выплаты проводятся два раза в год, то формула (2.4) примет вид:
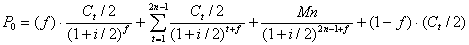
Вычислим величину f:
число дней между датой покупки и следующей купонной выплатой
f = ¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾ =
число дней в разорванном купонном периоде
=![]()
(В числителе указаны 19 дней в сентябре, без учета дня покупки, 31 день в октябре, 30 дней в ноябре и 1 декабря – день купонной выплаты. В знаменателе приведено число дней в разорванном купоном периоде – 29 дней в июне, без учета дня предыдущей купонной выплаты, 31 день в июле и т. д.).
Тогда:
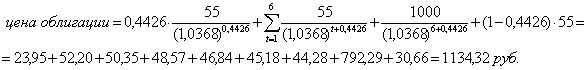
Как видим, полная цена облигации превосходит цену ее котировки (110,37 составляет 1103,7 руб.) точно на величину накопленного купона: 1134,32 = 1103,70 + 30,66; несовпадение объясняется проводимыми округлениями.
Условие 3: облигация сохраняется инвестором вплоть до её погашения.
Если предположить, что снимается это ограничение, и инвестор заведомо знает, что облигация не будет сохраняться им до погашения, то, строго говоря, текущая рыночная (котировочная) цена облигации никак не зависит от его решения. Для инвестора важнее оценить предполагаемую цену продажи облигации. Способы такой оценки рассматриваются ниже.
2.2. Взаимосвязь между ценой облигации, купонной выплатой, ставкой дисконта и сроком погашения.
При анализе портфеля облигаций обычно оперируют чистой (котировальной) ценой облигации, выводя накопленный купонный доход за рамки анализа. Такая практика оправдана: использование чистой цены облигации значительно упрощает теоретические модели управления портфелем облигаций. Учесть же НКД можно в конце всех оценок, добавив его к чистой цене. Анализ чистой цены облигации позволяет установить важные соотношения между параметрами, воздействующими на цену облигацию
Вернемся к облигации А (номинал ![]() = 1000р., купонная ставка
= 1000р., купонная ставка ![]() = 5%, ставка дисконта
= 5%, ставка дисконта ![]() = 7%, срок погашения
= 7%, срок погашения ![]() = 20 лет). Выясним, как реагирует чистая цена облигации на изменения ее параметров – купонной ставка
= 20 лет). Выясним, как реагирует чистая цена облигации на изменения ее параметров – купонной ставка ![]() , ставки дисконта
, ставки дисконта ![]() и срока погашения
и срока погашения ![]() . Полученные данные сведем в таблицу 2-1, где данные по исходной облигации выделены (купонные выплаты и номинал оцениваются в рублях):
. Полученные данные сведем в таблицу 2-1, где данные по исходной облигации выделены (купонные выплаты и номинал оцениваются в рублях):
Таблица 1.
Зависимость цены облигации от ее основных параметров
Ct = i = 5%
i = 7%>Ct
i = 3%<Ct
Годы до
погашения
PV
купонных
выплат
PV
номинала
Цена
Po
PV
купонных
выплат
PV
номинала
Цена
Po
PV
купонных
выплат
PV
номинала
Цена
Po
20
623,1
376,9
1000
529,7
258,4
788,1
743,9
553,7
1297,6
15
519,0
481,0
1000
455,4
365,4
820,8
596,9
641,9
1238,8
10
386,1
613,9
1000
351,2
508,3
859,5
426,5
744,1
1170,6
5
216,5
783,5
1000
205,0
713,0
918,0
229,0
862,6
1091,6
1
48,6
952,4
1000
46,7
934,6
981,3
48,5
970,9
1019,4
0
0
1000
1000
0
1000
1000
0
1000
1000
Данные таблицы 1 позволяют сделать важные выводы:
1) Цена облигации Po и ставка дисконта (доходность к погашению) i находятся в обратной зависимости – при прочих равных условиях повышение (понижение) величины i приводит к падению (росту) цены Po. Действительно, если срок до погашения ![]() = 20 лет, то, как следует из таблицы, повышение ставки дисконта с 5% до 7% приводит к снижению цены облигации от 1000 руб. до 788,1 руб., а падение ставки
= 20 лет, то, как следует из таблицы, повышение ставки дисконта с 5% до 7% приводит к снижению цены облигации от 1000 руб. до 788,1 руб., а падение ставки ![]() до 3% вызывает рост цены облигации до 1297,6 руб. То же наблюдается и при других сроках погашения облигации.
до 3% вызывает рост цены облигации до 1297,6 руб. То же наблюдается и при других сроках погашения облигации.
2) В любой момент времени существует строгая взаимосвязь между чистой ценой облигации Po, купонной выплатой ![]() (выраженной в виде процента) и ставкой дисконта (доходностью к погашению)
(выраженной в виде процента) и ставкой дисконта (доходностью к погашению) ![]() :
:
- когда процент ![]() купонной выплаты равняется
купонной выплаты равняется ![]() , то цена облигации Po равняется номинальной стоимости
, то цена облигации Po равняется номинальной стоимости ![]() . Действительно, как видно из таблицы, при величине
. Действительно, как видно из таблицы, при величине ![]() =
= ![]() = 5% цена облигации равна номиналу
= 5% цена облигации равна номиналу ![]() = 1000 руб. вне зависимости от срока погашения облигации. Величины номинала
= 1000 руб. вне зависимости от срока погашения облигации. Величины номинала ![]() и процента купонной выплаты
и процента купонной выплаты ![]() задаются изначально в момент эмиссии и не меняются вплоть до погашения облигации, а ставка
задаются изначально в момент эмиссии и не меняются вплоть до погашения облигации, а ставка ![]() и текущая цена Po облигации могут меняться под воздействием рыночных факторов. Поэтому справедливо и обратное утверждение - всякий раз, когда цена облигации совпадает с ее номиналом, доходность к погашению облигации
и текущая цена Po облигации могут меняться под воздействием рыночных факторов. Поэтому справедливо и обратное утверждение - всякий раз, когда цена облигации совпадает с ее номиналом, доходность к погашению облигации ![]() (ставка дисконта) равняется проценту купонных выплат;
(ставка дисконта) равняется проценту купонных выплат;
- когда купонная ставка процента ![]() выше величины
выше величины ![]() , цена облигации превосходит ее номинальную стоимость вне зависимости от срока погашения облигации. Это видно из раздела таблицы (9-1), когда
, цена облигации превосходит ее номинальную стоимость вне зависимости от срока погашения облигации. Это видно из раздела таблицы (9-1), когда ![]() = 5%, а
= 5%, а ![]() = 3%. В этом случае владелец облигации может продать ее и получить премию по отношению к номиналу;
= 3%. В этом случае владелец облигации может продать ее и получить премию по отношению к номиналу;
- в случае, когда купонная ставка ![]() становится ниже
становится ниже ![]() , то чистая цена облигации будет меньше номинала – об этом свидетельствуют данные таблицы при
, то чистая цена облигации будет меньше номинала – об этом свидетельствуют данные таблицы при ![]() = 5% и
= 5% и ![]() = 7%. Если у инвестора появится необходимость в этот момент продать облигацию, то считается, что он сделал это с дисконтом по отношению к номиналу. Этот дисконт представляет собой разницу между рыночной ценой облигации Po и ее номинальной стоимостью. Например, при
= 7%. Если у инвестора появится необходимость в этот момент продать облигацию, то считается, что он сделал это с дисконтом по отношению к номиналу. Этот дисконт представляет собой разницу между рыночной ценой облигации Po и ее номинальной стоимостью. Например, при ![]() =7%,
=7%, ![]() =5% и оставшимся сроком до погашения 15 лет, цена облигации падает до 820,8 руб., и дисконт составит 179,2 руб.. Если подобная ситуация сохранится до момента погашения, то дисконт покажет ту выгоду, которую получил инвестор за то, что не ликвидировал досрочно облигацию, купонная выплата которой
=5% и оставшимся сроком до погашения 15 лет, цена облигации падает до 820,8 руб., и дисконт составит 179,2 руб.. Если подобная ситуация сохранится до момента погашения, то дисконт покажет ту выгоду, которую получил инвестор за то, что не ликвидировал досрочно облигацию, купонная выплата которой ![]() =5% была ниже рыночной доходности в 7%.
=5% была ниже рыночной доходности в 7%.
3) Цена облигации зависит от срока, оставшегося до ее погашения, причем эта зависимость определяется соотношением купонной ставки процента и доходности к погашению. Как следует из таблицы (2-1), если купонная выплата ![]() равняется
равняется ![]() , то цена облигации вне зависимости от срока, оставшегося до погашения, всегда равна номинальной стоимости 1000 руб. Если же
, то цена облигации вне зависимости от срока, оставшегося до погашения, всегда равна номинальной стоимости 1000 руб. Если же ![]() ≠
≠![]() , то цена облигации Po равняется номиналу только в момент ее погашения. При этом, когда облигация имеет дисконт, то есть
, то цена облигации Po равняется номиналу только в момент ее погашения. При этом, когда облигация имеет дисконт, то есть ![]() <
< ![]() , то цена облигации постепенно повышается по мере приближения срока погашения; когда
, то цена облигации постепенно повышается по мере приближения срока погашения; когда ![]() >
> ![]() и облигация может быть продана с премией, то цена облигации медленно падает с приближением срока погашения.
и облигация может быть продана с премией, то цена облигации медленно падает с приближением срока погашения.
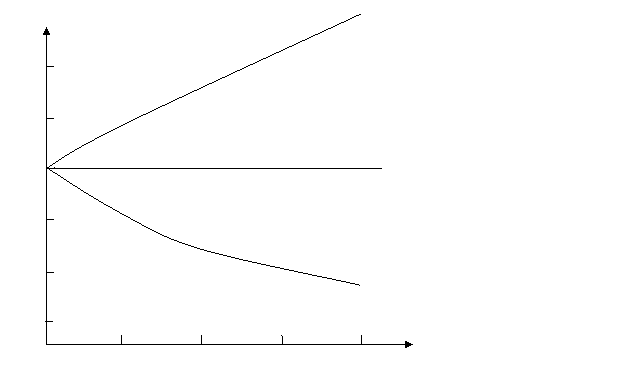
Соотношение цены облигации и срока, оставшегося до ее погашения, характеризует рисунок 1:
 Цена облигации (руб.)
Цена облигации (руб.) ![]() >
> ![]()
1200
1100
1000 Ct = i
900
800 Ct < ![]()
700
5 лет 10 лет 15 лет 20 лет срок до погашения
Рисунок 1. Соотношение цены облигации и срока ее погашения
при различных величинах ![]() и
и ![]() .
.
На данном рисунке соответствующие величины цен облигации взяты из таблицы 2-1.
Для быстрой оценки цены облигации полезна следующая формула:
![]()
При этом величины номинала, купонной ставки и ставки дисконта надо брать в процентных величинах.
Пример: Вернемся к таблице 1 и оценим по этой формуле цену облигации со сроком погашения ![]() = 5 лет,
= 5 лет, ![]() = 5%,
= 5%, ![]() = 3%:
= 3%:
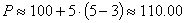
что достаточно близко к истинной цене 109.16.
Тема 3
Оценка доходности и отдачи облигации.
Особенностью анализа облигации является использование нескольких видов доходности. Кроме того, для умелого управления портфелем облигаций большое значение имеют составляющие их отдачи (дохода). Остановимся на этих категориях подробно.
3.1. Основные виды доходности облигации.
Существует несколько видов доходности облигаций, из которых наиболее часто применяются:
а) номинальная, или купонная доходность;
б) текущая доходность;
в) доходность к погашению
г) доходность к моменту отзыва
Номинальная доходность (купонная ставка) показывает процентную величину суммарного ежегодного дохода, полученного от облигации в виде купонных выплат, по отношению к номинальной стоимости облигации:
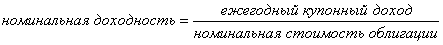
Номинальная доходность позволяет оценить ту ежегодную сумму, которую получит инвестор в виде процента по облигации: если купонная ставка ![]() = 4%, следовательно, ежегодно по облигации выплачивается в виде процента (купонной выплаты) 0,04 номинальной стоимости облигации.
= 4%, следовательно, ежегодно по облигации выплачивается в виде процента (купонной выплаты) 0,04 номинальной стоимости облигации.
Несмотря на большое значение, которое играет номинальная доходность в анализе облигаций, эта величина имеет два существенных недостатка, ограничивающие возможности ее использования:
· Во-первых, при вычислении номинальной доходности используется номинальная стоимость и не учитывается текущая цена облигации. В этой связи оценка облигации только по ее номинальной доходности может привести к неверному инвестиционному решению. Например, на рынке имеются облигации двух типов – первые имеют номинальную доходность 7,5% и продаются по номиналу; у вторых облигаций номинальная доходность 7%, и они продаются по 900 руб. Инвестор располагает 9000 руб. и может купить либо девять облигаций первого типа, либо десять – второго. Что выгоднее? Использование номинальной доходности не дает точного ответа: приобретение облигаций первого типа с более высокой номинальной доходностью менее выгодно, т. к. девять облигаций этого типа обеспечивают: 75 руб.×(9 облигаций) = 675 руб. купонных сумм. Если купить десять облигаций второго типа, то на те же 9000 руб. инвестиционных затрат они дадут 700 руб. купонных выплат, что выгоднее первого варианта.
· Во-вторых, номинальная доходность оставляет в стороне иные, кроме купонных выплат, составляющие отдачи облигации, которые может обеспечить облигация.
Текущая доходность устраняет первый недостаток номинальной доходности, так как при ее исчислении используется не номинальная, а текущая рыночная цена облигации:
![]()
Текущая доходность широко используется при оценке облигаций; особенно полезна она бывает тем инвесторам, для которых имеет принципиальное значение величина ежегодного купонного дохода в расчете на один инвестированный рубль.
Но текущая доходность также не устраняет второй недостаток, оставляя в стороне иные компоненты отдачи облигаций.
Доходность к погашению (yield to maturity - YTM) является наиболее часто употребляемой мерой оценки доходности облигаций, поскольку она устраняет оба недостатка, присущих номинальной и текущей доходности. Существует несколько эквивалентных определений доходности к погашению. Чтобы был более понятен смысл этих определений, рассмотрим три условные облигации A, B, C, имеющие одинаковую номинальную стоимость 1000 руб.:
- облигация А - бескупонная, срок погашения 1 год, цена 930,23 руб.;
- облигация В - бескупонная, срок погашения 2 года, цена 849,46 руб.;
- облигация С - купонная, срок погашения 2 года, купонная ставка 6%, купоны выплачиваются раз в год, цена 963,70 руб..
Итак, приобретя облигацию А за 930,23 руб., инвестор через год получит 1000 руб.; если он купит облигацию В за 849,46 руб., то 1000 руб. он получит через два года; наконец, приобретение облигации C за 963,7 руб. обеспечит инвестору процентную выплату через год в размере 60 руб., а через два года в момент погашения он получит еще одну процентную выплату 60 руб. плюс номинал, то есть 1060 руб.
Первое определение доходности к погашению основывается на предположении, что инвестор всегда имеет альтернативу вложить в банк деньги, предназначенные для покупки облигации. В таком случае, под доходностью к погашению облигации следует понимать ту единственную и неизменную ставку процента (с учетом начисления сложного процента через определенные промежутки времени), которая, будучи выплачиваемой банком на инвестированную сумму, обеспечивала бы инвестору получение тех платежей, которые предусмотрены условиями выпуска облигации. Например, в случае облигации А доходность к погашению ![]() составляет такую условную процентную ставку, что размещение под нее 930,23 руб. в банке принесет через год инвестору 1000 руб., то есть точно такую сумму, которая предусмотрена условиями эмиссии. Иными словами:
составляет такую условную процентную ставку, что размещение под нее 930,23 руб. в банке принесет через год инвестору 1000 руб., то есть точно такую сумму, которая предусмотрена условиями эмиссии. Иными словами:
(1+![]() )´930,23=1
)´930,23=1
откуда: 1+![]() = 1,075 и
= 1,075 и ![]() = 0,075 или 7,5%, что и составит величину доходности к погашению первой облигации.
= 0,075 или 7,5%, что и составит величину доходности к погашению первой облигации.
В случае облигации В альтернативное размещение в банке 849,46 руб. по ставке процента ![]() должно через год дать сумму (1+
должно через год дать сумму (1+![]() )´849,46 руб., а через два года с учетом сложного процента эта сумма составит: (1+
)´849,46 руб., а через два года с учетом сложного процента эта сумма составит: (1+![]() ) ´(1+
) ´(1+![]() ) ´849,46 руб., которая, по условиям выпуска, должна равняться 1000 руб.:
) ´849,46 руб., которая, по условиям выпуска, должна равняться 1000 руб.:
(1+![]() )´(1+
)´(1+![]() )´849,46=1
)´849,46=1
Откуда (1+![]() )2=1,1772, следовательно (1+
)2=1,1772, следовательно (1+![]() )=1,085 и
)=1,085 и ![]() =0,085 или 8,5%, что равняется доходности к погашению облигации В.
=0,085 или 8,5%, что равняется доходности к погашению облигации В.
Сложнее высчитать доходность к погашению облигации C. Представим, что в исходный момент на счете в банке размещаются 963,7 руб. Через год эта сумма должна возрасти до (1+![]() )´963,7 руб.. После этого инвестор получает в виде купонной выплаты 60 руб., и на счете у него остается [(1+
)´963,7 руб.. После этого инвестор получает в виде купонной выплаты 60 руб., и на счете у него остается [(1+![]() )´963,7 - 60] руб. Данная сумма еще через год даст инвестору на счете [(1+
)´963,7 - 60] руб. Данная сумма еще через год даст инвестору на счете [(1+![]() )´963,7-60]´(1+
)´963,7-60]´(1+![]() )]руб. По условию эмиссии облигации, это должно составлять 1060 руб.:
)]руб. По условию эмиссии облигации, это должно составлять 1060 руб.:
[(1+![]() )´963,7-60]´(1+
)´963,7-60]´(1+![]() )] = 1
)] = 1
откуда находим ![]() =0,08 или 8%. Значит доходность к погашению облигации С составляет 8%.
=0,08 или 8%. Значит доходность к погашению облигации С составляет 8%.
Чтобы вывести второе определение доходности к погашению облигации обратимся к равенствам (3.1-3.3). Разделим обе части равенства (3.1) на величину (1+![]() ):
):
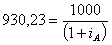 (3.4)
(3.4)
Аналогичные операции проведем с равенствами (3.2) и (3.3), только обе части равенства (3.2) разделим на величину (1+![]() )2, а равенства (3.3) - на (1+
)2, а равенства (3.3) - на (1+![]() )2:
)2:
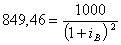 (3.5)
(3.5)
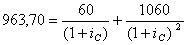 (3.6)
(3.6)
Выражения (3.4-3.6) представляют формулы для вычисления приведенной стоимости денежных потоков облигаций. Отсюда следует второе эквивалентное определение доходности к погашению: YTM – это такая ставка дисконта, при которой приведенная стоимость денежных потоков, обеспечиваемых облигацией (купонные выплаты и номинал), становится равной рыночной цене облигации Po на момент вычисления текущей стоимости. Подобное определение доходности к погашению эквивалентно понятию внутренней нормы доходности (internal rate of return - IRR) инвестиций. Значит, доходность к погашению представляет собой внутреннюю норму доходности IRR облигации.
Наконец, вернемся к равенству (3.6) и перепишем его в виде:
963,7´(1+![]() )2 = 60´(1+
)2 = 60´(1+![]() ) + 1
) + 1
Откуда: (1+![]() )2 = [60´(1+
)2 = [60´(1+![]() )+1060]/963,7 и, следовательно:
)+1060]/963,7 и, следовательно:
![]()
В знаменателе подкоренного выражения находится величина первоначальных инвестиционных затрат Po, или, если проводить аналогию с банковским счетом, сумма начального вклада Sначальная - 963,7 рублей. Числитель же представляет тот суммарный доход Sконечная, который инвестор может получить за два года. Действительно, через год он получит 60 руб. в виде процентных выплат, и может реинвестировать их (положить в банк) по той же ставке процента ![]() . Через два года первая купонная выплата обеспечит инвестору сумму 60´(1+
. Через два года первая купонная выплата обеспечит инвестору сумму 60´(1+![]() ) руб. Кроме того, через два года в момент погашения облигация обеспечит еще 60 руб. второй купонной выплаты плюс 1000 руб. номинала. Итого за два года облигация может дать инвестору сумму [60´(1+ic)+1060] руб. В таком случае из выражения (3.8) можно вывести третье альтернативное определение доходности к погашению: YTM - это средняя геометрическая годовая доходность iсред. геометр., которую инвестор ожидает получить от своей инвестиции в момент покупки облигации, рассчитывая держать облигацию вплоть до ее погашения.
) руб. Кроме того, через два года в момент погашения облигация обеспечит еще 60 руб. второй купонной выплаты плюс 1000 руб. номинала. Итого за два года облигация может дать инвестору сумму [60´(1+ic)+1060] руб. В таком случае из выражения (3.8) можно вывести третье альтернативное определение доходности к погашению: YTM - это средняя геометрическая годовая доходность iсред. геометр., которую инвестор ожидает получить от своей инвестиции в момент покупки облигации, рассчитывая держать облигацию вплоть до ее погашения.
Представим, что инвестор приобрел в какой-то конкретный день облигацию, заплатив за нее начальную цену Р0. Облигация имеет номинал 1000 руб., купонную ставку 5%, доходность к погашению 7% и срок погашения 5 лет. Чтобы обеспечить данную доходность к погашению как среднюю годовую геометрическую доходность инвестор должен все 5 лет реинвестировать получаемые купонные суммы. Так, через год он получит первую купонную выплату 50 руб., которую может реинвестировать по ставке 7% (равной доходности к погашению) на оставшиеся до погашения 4 года. В итоге к моменту погашения первая купонная выплата обеспечит получение суммы равной 50×(1,07)![]() . Аналогично, вторая купонная сумма может быть реинвестирована по ставке 7% на оставшиеся до погашения 3 года, и к моменту погашения даст инвестору 50×(1,07)
. Аналогично, вторая купонная сумма может быть реинвестирована по ставке 7% на оставшиеся до погашения 3 года, и к моменту погашения даст инвестору 50×(1,07)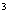 . В итоге, чтобы обеспечить данную доходность к погашению как среднюю годовую геометрическую доходность инвестор должен за 5 лет аккумулировать следующую сумму:
. В итоге, чтобы обеспечить данную доходность к погашению как среднюю годовую геометрическую доходность инвестор должен за 5 лет аккумулировать следующую сумму:
50×(1,07)![]() + 50×(1,07)
+ 50×(1,07)![]() + 50×(1,07)
+ 50×(1,07)![]() + 50×(1,07) + 50 + 1000 руб.
+ 50×(1,07) + 50 + 1000 руб.
Только в этом случае YTM будет представлять собой ту геометрическую среднюю ежегодную доходность, которая уравняет сложный процент Р0×(1,07)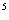 первоначальных инвестиционных затрат с общей суммой полученного от облигации дохода, то есть:
первоначальных инвестиционных затрат с общей суммой полученного от облигации дохода, то есть:
Р0×(1,07)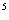 = 50×(1,07)
= 50×(1,07)![]() + 50×(1,07)
+ 50×(1,07)![]() + 50×(1,07)
+ 50×(1,07)![]() + 50×(1,07) + 50 + 1000 руб.
+ 50×(1,07) + 50 + 1000 руб.
и удовлетворится равенство:
YTM = 0,07 = 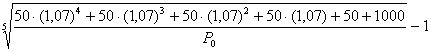
Отсюда можно вычислить, что в момент покупки цена облигации составляла 918 руб.
Обратим внимание на принципиальный момент, часто ускользающий от внимания инвесторов: несмотря на то, что доходность к погашению YTM рассматривается как средняя геометрическая доходность, в реальности YTM – это условная, ожидаемая (в смысле предполагаемая), или обещанная величина, которая будет обеспечиваться в долгосрочном периоде только в случае выполнения следующих условий:
1) эмитент выплачивает все купонные (процентные) суммы и номинал в соответствии с условиями выпуска облигации;
2) инвестор сохраняет облигацию до момента ее погашения;
3) все суммы купонных выплат сразу же после их получения реинвестируются владельцем облигации по ставке процента, равной YTM.
Из этих трех условий самым принципиальным является последнее: чтобы обеспечить заданную доходность к погашению YTM как среднюю геометрическую годовую доходность, владелец облигации должен реинвестировать все суммы купонных выплат по ставке процента, равной YTM, сразу по получении купонной выплаты.
Пример 5: пусть имеется облигация сроком погашения 10 лет, ежегодной купонной ставкой ![]() = 5%, рыночная цена которой
= 5%, рыночная цена которой ![]() = 110.00. Чему равна доходность к погашению данной облигации? Так как YTM является IRR облигации, то величину доходности к погашению надо находить из выражения:
= 110.00. Чему равна доходность к погашению данной облигации? Так как YTM является IRR облигации, то величину доходности к погашению надо находить из выражения:
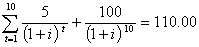
Обычная практика, используемая при этом для вычисления доходности к погашению ![]() , это метод проб и ошибок, поскольку уравнения подобного рода неразрешимы обычным алгебраическим путем. Как следует поступить в нашем случае? Если рыночная стоимость облигации выше номинала, то ставка дисконта
, это метод проб и ошибок, поскольку уравнения подобного рода неразрешимы обычным алгебраическим путем. Как следует поступить в нашем случае? Если рыночная стоимость облигации выше номинала, то ставка дисконта ![]() (а для нас она, в том числе, и доходность к погашению, требуемая доходность) должна быть ниже процента купонных выплат
(а для нас она, в том числе, и доходность к погашению, требуемая доходность) должна быть ниже процента купонных выплат ![]() . Предположим сначала
. Предположим сначала ![]() =3% и, проведя соответствующие вычисления, найдем, что приведенная стоимость денежных потоков облигации в этом случае будет составлять 117.06, что выше рыночной цены. Значит, величина
=3% и, проведя соответствующие вычисления, найдем, что приведенная стоимость денежных потоков облигации в этом случае будет составлять 117.06, что выше рыночной цены. Значит, величина ![]() = 3% ниже искомой доходности к погашению. Тогда примем
= 3% ниже искомой доходности к погашению. Тогда примем ![]() = 4% и высчитаем, что в этом случае приведенная стоимость денежных потоков облигации составит 109.11, что уже ниже рыночной цены. Значит, истинное значение доходности к погашению
= 4% и высчитаем, что в этом случае приведенная стоимость денежных потоков облигации составит 109.11, что уже ниже рыночной цены. Значит, истинное значение доходности к погашению ![]() находится в пределах от 3% до 4%.
находится в пределах от 3% до 4%.
Приблизительную величину ![]() можно найти по формуле:
можно найти по формуле:
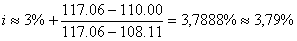
Что означает эта цифра? Ее надо понимать следующим образом: если инвестор купит облигацию за 110.00 (то есть вложит в нее сумму Sначальн.= 1100 руб.), будет держать ее вплоть до момента погашения и получать в обещанные эмитентом сроки положенные суммы купонных выплат, которые тут же будет реинвестировать под 3,79%, то через десять лет при погашении облигации и получении номинала его суммарный доход Sконечн., равный (номинал + купонные выплаты + процент на процент), станет таковым, что выполнится условие:
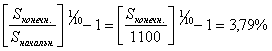
то есть 3,79% будут представлять среднюю геометрическую ежегодную доходность.
Не представляет труда вычислить доходность к погашению бескупонных облигаций. Например, если рыночная цена бескупонной облигации сроком погашения 5 лет составляет 72.99, то доходность к погашению ![]() такой облигации найдем из равенства:
такой облигации найдем из равенства:
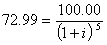
Расчеты дают величину ![]() = 0,065 или 6,5%. Поскольку по бескупонной облигации ежегодные выплаты не делаются, то требование обязательного реинвестирования получаемых сумм в этом случае неприменимо. Если инвестор купит бескупонную облигацию и будет держать ее до момента погашения, то он получит доходность к погашению, которая наблюдалась на момент приобретения облигации (ниже будет показано, что эта величина может меняться непрерывно).
= 0,065 или 6,5%. Поскольку по бескупонной облигации ежегодные выплаты не делаются, то требование обязательного реинвестирования получаемых сумм в этом случае неприменимо. Если инвестор купит бескупонную облигацию и будет держать ее до момента погашения, то он получит доходность к погашению, которая наблюдалась на момент приобретения облигации (ниже будет показано, что эта величина может меняться непрерывно).
Доходность к моменту отзыва используется в тех случаях, когда эмитент заранее предупреждает инвестора, что в случае обусловленного снижения доходности к погашению и роста цены облигации эти облигации будут выкуплены эмитентом. Обычная практика в таких случаях - это установление эмитентом заранее графика отзыва облигации и цен отзыва (call price). В общем случае под доходностью к моменту отзыва надо понимать ту ставку дисконта, которая делает приведенную стоимость будущего потока денег (купонные выплаты плюс цена отзыва) равной рыночной цене облигации ![]() :
:
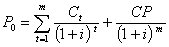
где: m - количество лет до отзыва;
CP - цена отзыва;
![]() - доходность к моменту отзыва.
- доходность к моменту отзыва.
Пример 6: инвестор приобрел облигацию рыночной стоимостью 85.00, купонная ставка ![]() = 9% выплачивается ежегодно; по условиям выпуска, облигация подлежит отзыву через 5 лет по цене отзыва 103 (то есть 1030 руб.). Доходность к моменту отзыва определится из уравнения:
= 9% выплачивается ежегодно; по условиям выпуска, облигация подлежит отзыву через 5 лет по цене отзыва 103 (то есть 1030 руб.). Доходность к моменту отзыва определится из уравнения:

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 |





