МОДЕЛЬ МУЛЬТИПЛИКАТОРА В ТЕОРИИ
КРЕАТИВНОГО БЛАГОСОСТОЯНИЯ
В концепции креативной ценности высшая, творческая, деятельность человека рассматривается в качестве абсолютного блага (от англ. creative -творческий, созидательный). Величина креативного благосостояния индивида за некоторый период измеряется суммарным временем его высшей деятельности. По сути, индивидуальное благосостояние отождествляется со свободным временем человека, заполненным высшей деятельностью. Общее благосостояние равно сумме значений индивидуального благосостояния всех членов общества, поэтому функция общего благосостояния в креативной теории является аддитивной. Это не означает, что увеличение благосостояния какого-либо индивида на некоторую величину вызовет увеличение общего благосостояния на ту же величину. Индивиды воздействуют друг на друга, и изменение благосостояния одного из них может вызвать изменение благосостояния другого. Например, увеличение свободного времени матери позволяет ей проводить больше времени со своим сыном, и его жизнь становится более содержательной, т. е. увеличение благосостояния матери влечет за собой увеличение благосостояния сына. Сын, в свою очередь, воздействует на мать, и индуцированное увеличение его благосостояния вызовет некоторый рост ее благосостояния, и так далее до бесконечности. Процесс последовательных изменений значений благосостояния индивидов и сопутствующие изменения общего благосостояния представляют собой процесс мультипликации, который открыл и исследовал Джон Кейнс на примере мультипликации национального дохода, порожденной инвестиционным импульсом. В нашем случае эффект мультипликации заключается в том, что суммарный прирост общего благосостояния, достигнутый за бесконечный промежуток времени в результате разового увеличения благосостояния одного индивида, или в результате благотворного импульса, превосходит величину этого импульса. Мультипликатор общего благосостояния индивида есть число, равное отношению прироста общего благосостояния к величине разового увеличения благосостояния данного индивида.
Модель мультипликатора общего благосостояния принципиально отличается от модели мультипликатора национального дохода тем, что в первом случае каждый член общества имеет свой мультипликатор, характеризующий его общественную значимость. У Кейнса же мультипликатор единственен и выступает в качестве макроэкономического показателя. Благотворный импульс в креативной теории трактуется как кратковременное изменение условий жизни индивида, вызвавшее резкое повышение творческой насыщенности его жизни. Примерами благотворного импульса служат курс интенсивного обучения, развивающее путешествие, творческое общение с другим человеком и др. Величина импульса измеряется приростом времени высшей деятельности за рассматриваемый краткосрочный период по сравнению с предыдущим периодом равной продолжительности.
Мультиплицированный прирост общего благосостояния складывается из мультиплицированных приростов индивидуального благосостояния всех членов общества. Мультиплицированный прирост индивидуального благосостояния рассчитывается как сумма бесконечно убывающей последовательности приростов, отнесенных к следующим друг за другом равным по величине краткосрочным периодам времени. Для простоты изложения мы определяем данный краткосрочный период как месяц. Нулевым считается месяц, в котором рассматриваемый индивид испытал благотворный импульс.
Центральное место в модели мультипликации общего благосостояния играет матрица воздействий ![]() , ее элемент
, ее элемент ![]() равен приросту благосостояния
равен приросту благосостояния ![]() -го индивида в последующем месяце при увеличении на единицу благосостояния
-го индивида в последующем месяце при увеличении на единицу благосостояния ![]() -го индивида в текущем месяце. Данный элемент матрицы воздействия мы называем предельной нормой воздействия
-го индивида в текущем месяце. Данный элемент матрицы воздействия мы называем предельной нормой воздействия ![]() -го индивида на
-го индивида на ![]() -го индивида, он характеризует способность одного индивида воздействовать на другого индивида. Так, для популярного певца многие значения предельной нормы воздействия строго положительны, поскольку увеличение его креативного благосостояния позитивным образом сказывается на результатах его творческой деятельности, и поэтому содержательность жизни многочисленных поклонников увеличивается. Для "простого" члена общества число ненулевых значений предельной нормы воздействия невелико, они соответствуют членам его семьи, друзьям, коллегам и пр. Значения предельной нормы воздействия, как правило, неотрицательны. Однако нельзя исключать социальное поведение, когда увеличение благосостояния одного индивида вызывает сокращение благосостояния другого индивида. В этом случае, который в статье не рассматривается, предельная норма воздействия отрицательна.
-го индивида, он характеризует способность одного индивида воздействовать на другого индивида. Так, для популярного певца многие значения предельной нормы воздействия строго положительны, поскольку увеличение его креативного благосостояния позитивным образом сказывается на результатах его творческой деятельности, и поэтому содержательность жизни многочисленных поклонников увеличивается. Для "простого" члена общества число ненулевых значений предельной нормы воздействия невелико, они соответствуют членам его семьи, друзьям, коллегам и пр. Значения предельной нормы воздействия, как правило, неотрицательны. Однако нельзя исключать социальное поведение, когда увеличение благосостояния одного индивида вызывает сокращение благосостояния другого индивида. В этом случае, который в статье не рассматривается, предельная норма воздействия отрицательна.
Роль матрицы воздействий в модели мультипликации общего благосостояния аналогична роли матрицы прямых затрат в линейной балансовой модели В. Леонтьева. Обе матрицы описывают систему прямых взаимосвязей экономических субъектов в краткосрочном периоде: в первой модели субъектом является индивид, а во второй – отрасль, производящая один продукт. Диагональные элементы обеих матриц не превышают единицы.
Предположим, что в нулевом месяце ![]() -й индивид испытал благотворный импульс
-й индивид испытал благотворный импульс ![]() . Тогда вектор приростов индивидуальных благосостояний в нулевом месяце
. Тогда вектор приростов индивидуальных благосостояний в нулевом месяце ![]() состоит из нулевых координат за исключением
состоит из нулевых координат за исключением ![]() -й. В первом месяце индивидуальное благосостояние увеличится у всех индивидов, для которых предельная норма воздействия первого индивида строго положительна. Вектор приростов индивидуальных благосостояний в первом месяце определится по формуле
-й. В первом месяце индивидуальное благосостояние увеличится у всех индивидов, для которых предельная норма воздействия первого индивида строго положительна. Вектор приростов индивидуальных благосостояний в первом месяце определится по формуле
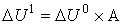 .
.
Обобщив данную формулу, получим, что вектор приростов индивидуальных благосостоянии в k-м месяце равен произведению вектора приростов индивидуальных благосостояний в нулевом месяце, умноженному справа на (k-1)-ю степень матрицы воздействий. Вектор приростов индивидуальных благосостояний за бесконечный период времени ![]() равен сумме бесконечной последовательности векторов месячных приростов:
равен сумме бесконечной последовательности векторов месячных приростов:
![]() .
.
Предположим, что сумма бесконечной матричной последовательности в полученном соотношении существует, тогда формула результирующего вектора индивидуальных приростов благосостояния за бесконечный период запишется как
![]() , (1)
, (1)
где ![]() - матрица, обратная матрице
- матрица, обратная матрице ![]() . Результирующий прирост общего благосостояния
. Результирующий прирост общего благосостояния ![]() за бесконечный период времени равен сумме координат вектора
за бесконечный период времени равен сумме координат вектора ![]() .
.
Прежде, чем выяснить экономический смысл матрицы ![]() , введем ряд понятий. Частный мультипликатор воздействия
, введем ряд понятий. Частный мультипликатор воздействия ![]() -го индивида на
-го индивида на ![]() -го индивида
-го индивида ![]() определим как суммарный прирост индивидуального благосостояния
определим как суммарный прирост индивидуального благосостояния ![]() -го индивида за бесконечный период, вызванный единичным благотворным импульсом
-го индивида за бесконечный период, вызванный единичным благотворным импульсом ![]() -го индивида:
-го индивида:
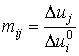 . (2)
. (2)
Матрицей частных мультипликаторов назовем матрицу ![]() , составленную из значений частных мультипликаторов воздействия всех индивидов. Мультипликатор общего благосостояния
, составленную из значений частных мультипликаторов воздействия всех индивидов. Мультипликатор общего благосостояния ![]() -го индивида
-го индивида ![]() определим как суммарный прирост общего благосостояния за бесконечный период, вызванным единичным благотворным импульсом данного индивида:
определим как суммарный прирост общего благосостояния за бесконечный период, вызванным единичным благотворным импульсом данного индивида:
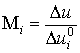 . (3)
. (3)
Понятно, что мультипликатор общего благосостояния индивида равен сумме всех его частных мультипликаторов воздействия на других индивидов, т. е. он равен сумме элементов соответствующей строки матрицы частных мультипликаторов.
Вернемся теперь к формуле (1). Из нее следует, что конечный прирост индивидуального благосостояния ![]() -го индивида в ответ на единичный благотворный импульс
-го индивида в ответ на единичный благотворный импульс ![]() -го индивида равен
-го индивида равен
![]() . (4)
. (4)
Сравнивая формулы (2) и (4), мы приходим к выводу, что матрица ![]() в формуле (1) совпадает с матрицей частных мультипликаторов
в формуле (1) совпадает с матрицей частных мультипликаторов ![]() , т. е. выполняется соотношение
, т. е. выполняется соотношение
![]() ,
,
которое представляет собой матричный аналог формулы мультипликации национального дохода в кейнсианской модели:
![]() ,
,
где ![]() - прирост национального дохода, вызванный инвестиционным импульсом
- прирост национального дохода, вызванный инвестиционным импульсом ![]() , а
, а ![]() - простой мультипликатор, вычисляемый по формуле
- простой мультипликатор, вычисляемый по формуле
![]() ,
,
где а - предельная склонность к потреблению. Мы видим, что матрица частных мультипликаторов в теории креативного благосостояния является аналогом простого мультипликатора в кейнсианской теории, поскольку она рассчитывается по аналогичной матричной формуле
![]() .
.
Роль матрицы частных мультипликаторов в креативной модели благосостояния аналогична роли матрицы полных затрат в линейной балансовой модели. Обе матрицы описывают систему взаимодействий соответствующих экономических субъектов в бесконечном периоде. Диагональные элементы обеих матриц не меньше единицы. Разность между некоторым диагональным элементом матрицы частных мультипликаторов и единицей характеризует индуцированный прирост благосостояния данного индивида при импульсном увеличении его благосостояния на единицу.
Распределение совокупного дохода в некотором месяце является общественно-оптимальным, если оно обеспечивает максимальный суммарный прирост общего благосостояния в долгосрочной перспективе. Выведем критерий оптимального распределения, или критерий креативной справедливости. Обозначим через ![]() зависимость индивидуального благосостояния
зависимость индивидуального благосостояния ![]() -го индивида от его дохода в нулевом месяце. Данная функция ограничена сверху продолжительностью суток, а ее производная характеризует прирост продолжительности высшей деятельности индивида, вызванный увеличением его дохода на единицу. Производную функции индивидуального благосостояния мы называем традиционным термином "предельная полезность" и обозначаем через
-го индивида от его дохода в нулевом месяце. Данная функция ограничена сверху продолжительностью суток, а ее производная характеризует прирост продолжительности высшей деятельности индивида, вызванный увеличением его дохода на единицу. Производную функции индивидуального благосостояния мы называем традиционным термином "предельная полезность" и обозначаем через ![]() . Но при этом необходимо помнить, что здесь под полезностью понимается креативная полезность, выраженная в часах высшей деятельности. С увеличением дохода способности индивида насыщать свое время творческой деятельностью сокращаются, и предельная полезность уменьшается. При некотором значении дохода индивид достигает своего творческого порога, а его креативное благосостояние - своего максимально возможного значения, при этом предельная полезность становится равной нулю.
. Но при этом необходимо помнить, что здесь под полезностью понимается креативная полезность, выраженная в часах высшей деятельности. С увеличением дохода способности индивида насыщать свое время творческой деятельностью сокращаются, и предельная полезность уменьшается. При некотором значении дохода индивид достигает своего творческого порога, а его креативное благосостояние - своего максимально возможного значения, при этом предельная полезность становится равной нулю.
Предположим, что в обществе имеются всего два индивида. Ставится задача оптимальным образом распределить между ними заданный дополнительный доход в нулевом месяце. Прирост дохода первого индивида в нулевом месяце ![]() , вызовет увеличение его креативного благосостояния в этом месяце на величину
, вызовет увеличение его креативного благосостояния в этом месяце на величину
![]() . (5)
. (5)
Выведем формулу прироста общего благосостояния в случае одновременного воздействия двух благотворных импульсов. Из формулы (3) следует, что мультипликатор общего благосостояния индивида равен частной производной функции общего благосостояния по величине импульса. Учитывая формулу (5), запишем суммарный прирост общего благосостояния за бесконечный период в виде линейной функции
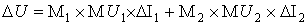 . (6)
. (6)
Распределение дополнительного фиксированного дохода является общественно-оптимальным, когда функция (6) принимает своей максимальное значение. Таким образом, проблема креативной справедливости сводится к задаче на условный экстремум. Решая ее методом Лагранжа, получим критерий оптимального распределения
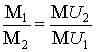 . (7)
. (7)
Из формулы (7) следует, что чем больше мультипликатор общего благосостояния индивида, тем меньше значение его предельной полезности, тем выше его общественно-оптимальный доход. Если функции индивидуального благосостояния обоих индивидов одинаковы, то индивид с большей величиной мультипликатора будет иметь больший общественно-оптимальный доход. Данный вывод служит этическим и теоретико-экономическим аргументом в пользу назначения относительно больших доходов известным людям творческих профессий: артистам, певцам, композиторам, писателям и пр.
Критерий креативной справедливости (7) напоминает по форме условие равновесия потребителя в традиционной микроэкономике. Однако в нашей модели порядок расстановки индексов в левой и правой частях равенства различен. Тем не менее, оба соотношения аналогичны по своей экономической сути, поскольку отражают прямую связь между ценностью объекта и его способностью создавать некоторый полезный эффект. В случае равновесия потребителя рост цены продукта означает снижение его способности создавать положительный эффект, поэтому при прочих равных условиях оптимальный объем потребления данного продукта сокращается. Иными словами, цена продукта противоположна его ценности для потребителя. В случае креативного равновесия рост общественной значимости индивида означает увеличение его способности создавать положительный эффект для общества в форме общего благосостояния, поэтому при прочих равных условиях оптимальный доход данного индивида увеличивается. Таким образом, мультипликатор общего благосостояния индивида отражает его общественную ценность.
Литература:
1. Творческая эволюция. М.: Канон-пресс, Кучково поле, 1998
2. Общая теория занятости, процента и денег. Петрозаводск: Петроком,1993
3. Корнейчук капитал во временном измерении. СПб.: Изд-во СПбГПУ, 2003
4. Корнейчук экономика. СПб.: Питер, 2006.
5. Korneichuk B. The Transformational Models of Consumption and Production: Towards an Institutional Microeconomics. Saint-Petersburg: State Polytechnic University, 2004




