Математика и информатика (стр. 5 )

При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, поэтому вводиться понятие интервальной оценки.

Определение 5. Интервальной называют оценку, которая определяется двумя числами – концами интервала.

Пусть Θ* – оценка неизвестного параметра Θ, полученная по данным выборки. Оценка тем точнее, чем меньше модуль разности Θ – Θ*. Если d > 0 и |Θ – Θ*| < d, то чем меньше d, тем точнее оценка Θ*, т. е. число d характеризует точность оценки. Заметим, что неравенство |Θ – Θ*| < d равносильно неравенству –d < Θ – Θ* < d или Θ* – d < Θ < Θ* + d.

Определение 6. Доверительной вероятностью (надёжностью) оценки Θ* параметра Θ называется вероятность γ, с которой осуществляется неравенство |Θ – Θ*| < d , т. е.

γ = P(|Θ – Θ*| < d ) или

γ = P(Θ* – d < Θ < Θ* + d),

означающее следующее: вероятность того, что интервал (Θ* – d, Θ* + d) заключает в себе неизвестный параметр Θ, равна γ.

Обычно доверительная вероятность задаётся заранее, причём в γ качестве берут число, близкое к единице. Наиболее часто надёжность задаётся равной 0.95, 0.99, 0.999.

Определение 7. Доверительным интервалом (Θ1, Θ2) для параметра Θ называется такой интервал, относительно которого с заранее выбранной вероятностью, близкой к единице, можно утверждать, что он содержит неизвестное значение параметра Θ. Концы доверительного интервала называются доверительными границами.

Доверительный интервал для оценки математического ожидания нормально распределенного признака (варианты) при известной дисперсии имеет вид:

,

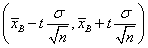где - выборочная средняя,

t – параметр, который находиться из условия , где Ф(t) – функция Лапласа, γ – заданная надежность.

σ - заданная дисперсия нормального распределения.

n – объем выборки.

При нахождении интервальных оценок решаются 3 основные задачи.

Задача 1. Дано: точность d, объём n. Найти: доверительную вероятность γ (надёжность).

Задача 2. Дано: доверительная вероятность γ, объём n. Найти: точность d.

Задача 3. Дано: точность d, доверительная вероятность γ. Найти: объём n.

Введение в информатику

·  Емкость человеческой памяти колеблется в широких пределах. Средняя величина - 1бит. Много это или мало? Во всем книжном фонде Российской государственной библиотеки в Москве информации 1013 бит, т. е. она могла уместиться в памяти одного человека;

·  Способность человека усваивать информацию (точнее, его скорость ввода информации в память) составляет в среднем 25 бит/с, или около одного слова в секунду. Скорость же работы современных ЭВМ перешагнула рубеж сотен миллионов бит в секунду;

·  Существует способ запоминания (ввода информации в человеческую память), называемый гипнопедия. Идея эта не нова. Так, еще в древней Греции учителя нашептывали спящим ученикам то, что трудно усваивалось днем. Его используют при обучении курсантов телеграфному коду в военно-морской школе во Флориде и летчиков во Франции. Глубокие исследования этого способа показали, что запоминание возможно лишь в наиболее поверхностные фазы сна, в период дремотного состояния.

·  Количество книг, которое может прочесть человек за всю жизнь, не превышает 6 - 8 тысяч. И это довольно высокая норма, которая предполагает ежедневное прочтения около 50 страниц. Но за время "читающей жизни" жизни книг будет издано более 20 миллионов, т. е. в среднем можно прочесть только одну из 10000 книг.

·  Английские исследователи утверждают, что о чувствах и мыслях человека на протяжении всей его жизни можно узнать с помощью микрочипа, встроенного в глазное яблоко.

Информатика – отрасль знаний, изучающая общие свойства и структуру информации, а также закономерности и принципы её создания, преобразования, накопления, передачи и использования в различных областях человеческой деятельности.

Информатика – наука, которая изучает процессы, связанные с получением, хранением, обработкой и передачей информации в обществе, в живой и неживой природе (компьютеры, различные технические устройства и тд.)

Кибернетика – наука об управлении, связи и переработке информации. Основным объектом являются абстрактные кибернетические системы: от компьютеров до человеческого мозга и человеческого общества.

Развитие вычислительной техники

В вычислительной технике существует своеобразная периодизация развития электронных вычислительных машин. ЭВМ относят к тому или иному поколению в зависимости от типа основных используемых в ней элементов или от технологии их изготовления. Ясно, что границы поколений в смысле времени сильно размыты, так как в одно и то же время фактически выпускались ЭВМ различных типов; для отдельной же машины вопрос о ее принадлежности к тому или иному поколению решается достаточно просто.

Появление ЭВМ или компьютеров – одна из существенных примет современной научно-технической революции. Широкое распространение компьютеров привело к тому, что все большее число людей стало знакомиться с основами вычислительной техники, а программирование постепенно превратилось в элемент культуры. Первые электронные компьютеры появились в первой половине XX века. Они могли делать значительно больше механических калькуляторов, которые лишь складывали, вычитали и умножали. Это были электронные машины, способные решать сложные задачи.

Кроме того, они имели две отличительные особенности, которыми предыдущие машины не обладали:

  I. Одна из них состояла в том, что они могли выполнять определенную последовательность операций по заранее заданной программе или последовательно решать задачи разных типов.

  II. Способность хранить информацию в специальной памяти.

Поколение первое. Компьютеры на электронных лампах.

Компьютеры на основе электронных ламп появились в 40-х годах XX века. Первая электронная лампа - вакуумный диод - была построена Флемингом лишь в 1904 году, хотя эффект прохождения электрического тока через вакуум был открыт Эдисоном в 1883 году. Вскоре Ли де Форрест изобретает вакуумный триод - лампу с тремя электродами, затем появляется газонаполненная электронная лампа - тиратрон, пятиэлектродная лампа - пентод и т. д. До 30-х годов электронные вакуумные и газонаполненные лампы использовались главным образом в радиотехнике. Но в 1931 году англичанин Винни-Вильямс построил (для нужд экспериментальной физики) тиратронный счетчик электрических импульсов, открыв тем самым новую область применения электронных ламп. Электронный счетчик состоит из ряда триггеров. Триггер, изобретенный -Бруевичем (1918) и - независимо - американцами У. Икклзом и Ф. Джорданом (1919), содержит 2 лампы и в каждый момент может находиться в одном из двух устойчивых состояний; он представляет собой электронное реле. Подобно электромеханическому, оно может быть использовано для хранения одной двоичной цифры. Подробнее об электронной лампе здесь.

Использование электронной лампы в качестве основного элемента ЭВМ создавало множество проблем. Из-за того, что высота стеклянной лампы - 7см, машины были огромных размеров. Каждые 7-8 мин. одна из ламп выходила из строя, а так как в компьютере их былотысяч, то для поиска и замены поврежденной лампы требовалось очень много времени. Кроме того, они выделяли огромное количество тепла, и для эксплуатации "современного" компьютера того времени требовались специальные системы охлаждения.

Чтобы разобраться в запутанных схемах огромного компьютера, нужны были целые бригады инженеров. Устройств ввода в этих компьютерах не было, поэтому данные заносились в память при помощи соединения нужного штеккера с нужным гнездом.

Примерами машин I-го поколения могут служить Mark 1, ENIAC, EDSAC (Electronic Delay Storage Automatic Calculator), - первая машина с хранимой программой. UNIVAC (Universal Automatic Computer). Первый экземпляр Юнивака был передан в Бюро переписи населения США. Позднее было создано много разных моделей Юнивака, которые нашли применение в различных сферах деятельности. Таким образом, Юнивак стал первым серийным компьютером. Кроме того, это был первый компьютер, где вместо перфокарт использовалась магнитная лента.

Поколение второе. Транзисторные компьютеры.

1 июля 1948 года на одной из страниц "Нью-Йорк Таймс", посвященной радио и телевидению, было помещено скромное сообщение о том, что фирма "Белл телефон лабораториз" разработала электронный прибор, способный заменить электронную лампу. Физик-теоретик Джон Бардин и ведущий экспериментатор фирмы Уолтер Брайттен создали первый действующий транзистор. Это был точечно-контактный прибор, в котором три металлических "усика" контактировали с бруском из поликристаллического германия.

Первые компьютеры на основе транзисторов появились в конце 50-х годов, а к середине 60-х годов были созданы более компактные внешние устройства, что позволило фирме Digital Equipment выпустить в 1965 г. первый мини-компьютер PDP-8 размером с холодильник (!!) и стоимостью всего 20 тыс. долларов (!!) .

Созданию транзистора предшествовала упорная, почти 10-летняя работа, которую еще в 1938 году начал физик теоретик Уильям Шокли. Применение транзисторов в качестве основного элемента в ЭВМ привело к уменьшению размеров компьютеров в сотни раз и к повышению их надежности.

И все-таки самой удивительной способностью транзистора является то, что он один способен трудиться за 40 электронных ламп и при этом работать с большей скоростью, выделять очень мало тепла и почти не потреблять электроэнергию. Одновременно с процессом замены электронных ламп транзисторами совершенствовались методы хранения информации. Увеличился объем памяти, а магнитную ленту, впервые примененную в ЭВМ Юнивак, начали использовать как для ввода, так и для вывода информации. А в середине 60-х годов получило распространение хранение информации на дисках. Большие достижения в архитектуре компьютеров позволило достичь быстродействия в миллион операций в секунду! Примерами транзисторных компьютеров могут послужить "Стретч" (Англия), "Атлас" (США). В то время СССР шел в ногу со временем и выпускал ЭВМ мирового уровня (например "БЭСМ-6").

Поколение третье. Интегральные схемы.

Подобно тому, как появление транзисторов привело к созданию второго поколения компьютеров, появление интегральных схем ознаменовало собой новый этап в развитии вычислительной техники - рождение машин третьего поколения. Интегральная схема, которую также называют кристаллом, представляет собой миниатюрную электронную схему, вытравленную на поверхности кремниевого кристалла площадью около 10 мм2. Подробнее об интегральных схемах здесь.

Первые интегральные схемы (ИС) появились в 1964 году. Сначала они использовались только в космической и военной технике. Сейчас же их можно обнаружить где угодно, включая автомобили и бытовые приборы. Что же качается компьютеров, то без интегральных схем они просто немыслимы!

Появление ИС означало подлинную революцию в вычислительной технике. Ведь она одна способна заменить тысячи транзисторов, каждый из которых в свою очередь уже заменил 40 электронных ламп. Другими словами, один крошечный кристалл обладает такими же вычислительными возможностями, как и 30-тонный Эниак! Быстродействие ЭВМ третьего поколения возросло в 100 раз, а габариты значительно уменьшились.

Ко всем достоинствам ЭВМ третьего поколения добавилось еще и то, что их производство оказалось дешевле, чем производство машин второго поколения. Благодаря этому, многие организации смогли приобрести и освоить такие машины. А это, в свою очередь, привело к росту спроса на универсальные ЭВМ, предназначенные для решения самых различных задач. Большинство созданных до этого ЭВМ являлись специализированными машинами, на которых можно было решать задачи какого-то одного типа.

Поколение четвертое. Большие интегральные схемы.

Вы уже знаете, что электромеханические детали счетных машин уступили место электронным лампам, которые в свою очередь уступили место транзисторам, а последние - интегральным схемам. Могло создастся впечатление, что технические возможности ЭВМ исчерпаны. В самом деле, что же можно еще придумать?

Чтобы получить ответ на этот вопрос, давайте вернемся к началу 70-х годов. Именно в это время была предпринята попытка выяснить, можно ли на одном кристалле разместить больше одной интегральной схемы. Оказалось, можно! Развитие микроэлектроники привело к созданию возможности размещать на одном-единственном кристалле тысячи интегральных схем. Так, уже в 1980 году, центральный процессор небольшого компьютера оказался возможным разместить на кристалле, площадью всего в четверть квадратного дюйма (1,61 см2). Началась эпоха микрокомпьютеров.

Каково же быстродействие современной микроЭВМ? Оно в 10 раз превышает быстродействие ЭВМ третьего поколения на интегральных схемах, в 1000 раз - быстродействие ЭВМ второго поколения на транзисторах и в 100000 раз - быстродействие ЭВМ первого поколения на электронных лампах.

Далее, почти 40 лет назад компьютеры типа Юнивак стоили около 2,5 млн. долларов. Сегодня же ЭВМ со значительно большим быстродействием, более широкими возможностями, более высокой надежностью, существенно меньшими габаритами и более простая в эксплуатации стоит примерно 2000 долларов. Каждые 2 года стоимость ЭВМ снижается примерно в 2 раза.

Очень большую роль в развитии компьютеров сыграли две ныне гигантские фирмы: Microsoft® и Intel®. Первая из них очень сильно повлияла на развитие программного обеспечения для компьютеров, вторая же стала известна благодаря выпускаемым ей лучшим микропроцессорам.

Сравнение разных поколений компьютеров.

Во время развития компьютеров четко обозначилась тенденция к уменьшению размеров и увеличению производительности. Чем более совершенствовалась элементная база компьютеров, тем меньше и быстрее они становились. Это можно показать на примере следуюшего сравнения и таблицы:

Сколько это в байтах

Этимология приставок не лишена интереса. Все началось в 1789 году, после Великой Французской революции, с переходом на метрическую систему. Тогда появились первые приставки «кило» (kilo, k, 103) и «мега» (mega, m, 106), и их вполне хватало. B XX веке, после Второй мировой войны, этот ряд приставок был продолжен, и появились две следующие: «гига» (giga, G) и «тера» (tera, T) — соответственно для 109 и 1012, то есть миллиард и триллион. В 1975 году Генеральная конференция мер и весов обогатила мир еще двумя приставками: «пета» (peta, P, 1015) и «экза» (exa, E, 1018), то есть квадриллион и квинтиллион. На этом процесс порождения приставок не остановился. В последнем издании Британской энциклопедии признаны права гражданства за «зетта» (zetta, Z, 1021) и «йота» (yotta, Y, 1024), то есть секстиллион и септиллион.

  Изначально приставки использовались для обозначения единиц измерения физических параметров в системе мер СИ. В ИТ те же самые приставки используются и для образования единиц измерения объемов информации при добавлении их к байтам. Уточним правило, принятое в английском языке. Для обозначения десятичных значений с приставками «кило» и «мега» используются только строчные буквы «к» и «м», а для двоичных чисел Kilo и Mega всегда заглавные «К» и «М».

  Приставки «кило», «мега», «гига» и «тера» имеют древнегреческое происхождение и соответственно означают «тысяча», «много», «гигант» и «монстр». Но есть и другое мнение, что tera образована от четверки: tetra. «Пета» (peta) представляет собой своеобразное сокращение греческой пятерки penta с исключением буквы n. Таким же образом была образована «экза» (exa), укороченная на h шестерка hexa.

  Названия «зетта» и «йотта» образованы от последней и предпоследней букв латинского алфавита.

[1] Если все точки лежат на вертикальной прямой, то уравнение линии имеет вид x = a.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5