P(A) = ![]() = 1– (1–
= 1– (1– ![]() )2 =
)2 = ![]()
Условная вероятность
Рассмотрим вопрос о том, как определить вероятность какого-либо события A при условии, что уже произошло другое событие B.
Например, пусть брошена игральная кость и нам неизвестен результат, но известно, что выпало четное число. Мы же хотим, зная эту информацию, подсчитать вероятность того, что выпало число больше трёх. Тогда речь идёт об условной вероятности события A= {выпало число больше трёх} при условии, что произошло событие B = {выпало чётное число}. Нам уже известно, что выпало либо 2, либо 4, либо 6 очков, и все эти исходы равновозможные. Среди этих исходов событию A удовлетворяют лишь исходы 4 и 6. Поэтому условной вероятностью естественно считать отношение 2/3.
Определение 1. Вероятность события A при условии, что произошло событие B, называется условной вероятностью и обозначается PВ(А).
Теорема 1. Вероятность совместного появления двух независимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило: ![]() .
.
Пример 1. В ящике m белых и n чёрных шаров. Шары тщательно перемешаны. Наудачу вынимаются сразу два шара. Какова вероятность того, что оба шара белые?
Решение. Достаточно вычислить вероятность события, которое представимо в виде произведения событий A= {1-й шар белый}, B = {2-й шар белый}. Итак, P(оба белые) = P(AB) = P(A)PА(В), где P(A) = m/(m+n), PА(В) = (m–1)/(m+n–1), следовательно,
P(оба белые) = 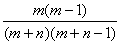 .
.
Определение 2. Событие A называется независимым от события B с P(B) ≠ 0, если P(A|B)= P(A), т. е. вероятность наступления события A не зависит от того, произошло ли B.
Пример 2. Пусть при бросании игральной кости A= {выпало число меньше трёх}, B = {выпало чётное число}. Поскольку A= {1, 2}, а B = {2, 4, 6}, то P(A) = ![]() и PА(В)=
и PА(В)= 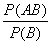 =
= ![]() =
= ![]() . Следовательно, событие A не зависит от события B.
. Следовательно, событие A не зависит от события B.
Лемма 1 (о взаимной независимости событий). Если событие A не зависит от события B при P(A) ≠ 0, P(B) ≠ 0, то и событие B не зависит от события A.
Итак, если события A и B не зависит друг от друга, то P(AB)=P(A) PА(В)=P(A)P(B).
Определение 3. События A и B называются независимыми, если вероятность одного из них не зависит от появления или не появления другого.
Формула полной вероятности и формула Байеса
При решении вероятностных задач часто возникает ситуация, когда пространство элементарных событий можно разбить на события, не содержащих общих исходов, и известно, каким образом вычислить условную вероятность события A, при условии, что произошли события этой группы, и вероятности событий самой группы. Нужно найти вероятность события A.
Определение. Набор событий В1, В2 ,…, Вn называется полной группой событий, если они попарно несовместны и их сумма составляет достоверное событие:
В1+В2+…+Вn = W.
Таким образом, всякое разбиение пространства W является полной группой событий. События В1, В2 ,…, Вn полной группы будем так же называть гипотезами.
Теорема 1 (формула полной вероятности). Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий В1, В2, …, Вn, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А: 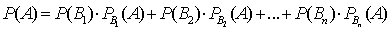 .
.
Пример 1. Пусть в коробке есть 3 новых и 3 уже использованных теннисных мяча. Для первой игры наудачу берут из коробки 2 мяча и затем их возвращают в коробку. Какова вероятность для второй игры из этой коробки наудачу вынуть два новых мяча?
Решение. Введём событие A ={вынуть два новых мяча для второй игры}. Ситуация после первой игры описывается следующими взаимоисключающими возможностями: В1 = {в коробке 1 новый мяч}, если играли двумя новыми, В2 = {в коробке 2 новых мяча}, если играли одним новым и одним старым, В3 = {в коробке 3 новых мяча}, если играли двумя старыми мячами. Подсчитаем P(В1) = C32/C62 = 1/5, P(В2)=3×3/C62=3/5, P(В3) =C32/C62=1/5. Далее PВ1(A)=0, PВ2(A)=1/C62=1/15, P(В1)= =C32/C62 = 1/5. Теперь, используя формулу полной вероятности
P(A) = ![]() ×0+
×0+![]() ×
×![]() +
+![]() ×
×![]() =
=![]() .
.
Теорема 2 (формула Байеса). Пусть событие А может наступить лишь при условии появления одного из несовместных событий (гипотез) В1, В2, …, Вn. Если событие А уже произошло, то вероятности гипотез могут быть найдены по формуле Байеса:
PА(Вk) = ![]() ,
,
где Р(А) – полная вероятность.
Пример 2. Два охотника одновременно и независимо стреляют в кабана. Известно, что первый попадает с вероятностью 0.8, а второй – 0.4. Кабан убит, и в нём обнаружена одна пуля. Как делить кабана?
Решение. Будем делить пропорционально условным вероятностям попадания каждого при условии, что в кабане имеется одна пуля. Пусть A ={в кабане имеется одна пуля}. Выберем полную группу событий: В00 = {оба не попали}, В10 = {попал первый}, В01 = {попал второй}, В11 = {оба попали}. Нам нужно найти PА(В10) и PА(В01). Очевидно, что PВ00 (A) = 0, PВ10 (A) = 1, PВ01 (A) = 1, PВ11 (A) = 0. Поскольку охотники стреляют независимо друг от друга, то по формуле умножения вероятностей P(В10) = P(попал первый) P(не попал второй) = 0.8×0.6 = 0.48, аналогично, P(В01) = 0.2×0.4 = 0.08. Применяя формулу Байеса, получим
PA (В10) = 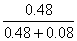 =
= ![]() , PA (В01) =
, PA (В01) = 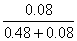 =
= ![]() .
.
Таким образом, первому следует отдать 6 долей из 7, а второму – одну.
Схема Бернулли
Схема Бернулли: проводятся n последовательных независимых одинаковых экспериментов (испытаний), в каждом из которых выделяется одно и то же событие A, которое может наступить или не наступить в ходе эксперимента. Так как испытания одинаковы, то в любом из них событие A наступает с одинаковой вероятностью, обозначим её p = P(A). Вероятность дополнительного события обозначим q. Тогда
q = P(![]() ) = 1– p.
) = 1– p.
Пример 1. Игральная кость бросается три раза. При каждом бросании нас интересует событие A ={выпала шестёрка}. В этом случае p = P(A) = 1/6, q = P(![]() ) = 5/6.
) = 5/6.
Теорема (формула Бернулли). Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < p < 1), событие наступит ровно к раз, равна
Pn(к) = Cnкpкqn–к.
Пример 2. Монету бросают 5 раз. Найти вероятность того, что герб выпадет менее двух раз.
Решение. р = ½ => q = ½.
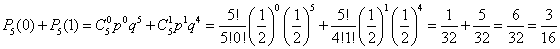
Случайные величины. Основные определения.
Определение 1. Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.
Обозначать случайные величины будем заглавными латинскими буквами X, Y, …, а конкретные их значения соответствующими строчными буквами x, y, … . Например, если случайная величина Х имеет три возможных значения, то они будут обозначены так: х1, х2, х3.
Определение 2. Дискретное (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значение с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или счетным (бесконечным).
Пример 1. Число родившихся мальчиков среди ста новорожденных есть случайная величина, которая имеет следующие значения: 0, 1, 2, …, 100.
Определение 3. Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Очевидно, число возможных значений непрерывной случайной величины бесконечно.
Пример 2. Расстояние, которое пролетит снаряд при выстреле из орудия, есть случайная величина. Действительно, расстояние зависит не только от установки прицела, но и от многих других причин (силы, направлении ветра, температуры …), которые не могут быть полностью учтены. Возможные значения этой величины принадлежат некоторому промежутку (a, b).
Числовые характеристики дискретной случайной величины
На первый взгляд может показаться, что для задания дискретной случайной величины достаточно перечислить все ее возможные значения. В действительности это не так: случайные величины могут иметь одинаковые перечни возможных значений, а вероятности их различные. Поэтому для задания дискретной случайной величины не достаточно перечислить все ее возможные значения, нужно еще указать их вероятности.
Определение 1. Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями.
При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая – их вероятности:
|
Х |
х1 |
х2 |
… |
хn |
|
Р |
р1 |
р2 |
… |
рn |
причем сумма вероятностей второй строки таблицы равна единице: р1 + р2 + … + рn = 1.
Для наглядности закон распределения случайной величины можно изобразить и графически, для чего в прямоугольной системе координат строят точки (хi, pi), а затем соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения.
Пример 1. В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 50 р. и десять выигрышей по 1 р. Найти закон распределения случайной величины Х – стоимости возможного выигрыша для владельца одного лотерейного билета.
Решение. Напишем возможные значения Х: х1 = 50, х2 = 1, х3 = 0. Вероятности этих возможных значений таковы: р1 = 0,01, р2 = 0,1, р3 = 1 – (р1 + р2) = 0,89. Напишем закон распределения:
|
Х |
50 |
1 |
0 |
|
Р |
0.01 |
0,1 |
0.89 |
Пример 2. Бросается игральная кость. Найти закон распределения случайной величины Х - число выпавших очков после двух бросков.
Решение. X принимает значения: 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12. Всего элементарных исходов 36. Например, значению X = 7 соответствуют исходы: (1, 6), (6, 1), (2, 5), (5, 2), (3, 4), (4, 3). Откуда P(X = 7) = 6/36 = 1/6. В итоге получим следующий закон распределения этой величины:
|
Х |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Р |
1/36 |
2/36 |
3/36 |
4/36 |
5/36 |
6/36 |
5/36 |
4/36 |
3/36 |
2/36 |
1/36 |
Пример 3. Дискретная случайная величина X имеет закон распределения
|
X |
–2 |
–1 |
0 |
1 |
2 |
|
P |
0.1 |
0.2 |
0.3 |
0.3 |
0.1 |
Построить закон распределения случайной величины Y = X2+1.
Решение. Значение 1 величины Y принимает только тогда, когда величина X принимает значение 0, с вероятностью 0.3. Значение 2 величина Y принимает, если величина X принимает значение –1 или 1 с вероятностями 0.2 и 0.3 соответственно. Тогда эти вероятности нужно сложить, что даст вероятность события Y = 2. Аналогично вероятность того, что Y = 5 будет равна 0.1+0.1 = 0.2. Следовательно, закон распределения случайной величины Y = X2+1 имеет вид
|
Y |
1 |
2 |
5 |
|
P |
0.3 |
0.5 |
0.2 |
Определение 2. Математическим ожиданием дискретной случайной величины X называется число
М(X) = ![]() .
.
Замечание. Если случайная величина имеет счётное число значений, т. е. n = ∞, то говорят, что математическое ожидание существует, если ряд ![]() сходится, в противном случае говорят, что математического ожидания не существует. Величину М(|X|) =
сходится, в противном случае говорят, что математического ожидания не существует. Величину М(|X|) = ![]() называют абсолютным моментом дискретной случайной величины X.
называют абсолютным моментом дискретной случайной величины X.
Пример 4. Найти математическое ожидание случайной величины Х, зная ее закон распределения:
|
X |
–2 |
–1 |
0 |
1 |
2 |
|
P |
0.1 |
0.2 |
0.3 |
0.3 |
0.1 |
Решение. М(Х) = -2.0,1 – 1.0,2 + 0.0,3 + 1.0,3 + 2.0,1 = 0,1.
Замечание. Если X – дискретная случайная величина, принимающая n различных значений, и g(x) – некоторая функция, то случайная величина g(X) принимает значения g(xi) с вероятностями pi = P(X = xi), i = 1, 2,…, n. Поэтому М(g(X)) = 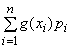 .
.
Свойства математического ожидания:
1) М(aX +b) = aМ(X)+b (свойство линейности) для любых постоянных a и b;
2) М(X+Y) = М(X) + М(Y) (свойство аддитивности) для любых двух случайных величин X и Y;
3) М(XY) = М(X)М(Y), если случайные величины независимы (но не наоборот);
4) если X ³ 0, то М(X) ³ 0, если X ³ Y, то М(X) ³ М(Y);
5) |М(X)| ≤ М(|X|) Для любой случайной величины X.
Определение 3. Дисперсией дискретной случайной величины X называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
D(X) = M(X – M(X))2 = M(X2) – M2(X) = 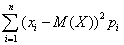 .
.
Смысл дисперсии заключается в том, что она характеризует средний квадратичный разброс случайной величины вокруг своего математического ожидания.
Пример 5. Найти дисперсию случайной величины Х, которая задана следующим законом распределения:
|
X |
–2 |
–1 |
0 |
1 |
2 |
|
P |
0.1 |
0.2 |
0.3 |
0.3 |
0.1 |
Решение. Имеем М(Х) = 0,1. Тогда D(X) = (-2 – 0,1)2.0,1 +,1)2.0,2 + (0 – 0,1)2.0,3 +,1)2.0,3 +,1)2.0,1 = 0,441 + 0,242 + 0,003 + 0,243 + 0,361 = 1,29.
Свойства дисперсии:
1) D(aX + b) = a2D(X) для любых постоянных a и b;
2) D(X + Y) = D(X) + D(Y), если случайные величины X и Y независимы;
3) D(X - Y) = D(X) + D(Y), если случайные величины X и Y независимы;
Определение 4. Средним квадратическим отклонением случайной величины называют квадратный корень из дисперсии: s(X) = 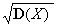 .
.
Законы распределения дискретной случайной величины
Биномиальным называют закон распределения дискретной величины Х – числа появления события в n последовательных независимых испытаниях, в каждом из которых вероятность появления события равна р; вероятность возможного значения Х = к (числа к появлений события) вычисляют по формуле Бернулли: Pn(к) = Cnкpкqn–к.
Вычисление математического ожидания и дисперсии дают следующие результаты:
М(X) = np; D(X) = np(1 – p) = npq; s(X) = ![]() .
.
Пример 1. В семье семь детей. Считая вероятность рождения мальчика и девочки равными 0.5, определить вероятность того, что в данной семье: а) три мальчика; б) менее трёх мальчиков; в) мальчиков не менее трёх, но и не более шести. Построить ряд распределения и найти значение функции распределения при x = 3.
Решение. Пусть X – число мальчиков.
а) P(X = 5) = C75(0.5)5×(0.5)7–5 » 0.164;
б) P(X < 3) = P(X = 0) + P(X = 1) + P(X = 2) = 0.227;
в) P(3 £ X £ 6) = P(X = 3) + P(X = 4) + P(X = 5) + P(X = 6) = 0.765.
|
Построим ряд распределения числа мальчиков. | ||||||||
|
Х |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Р |
0.008 |
0.055 |
0.164 |
0.273 |
0.273 |
0.164 |
0.055 |
0.008 |
Распределение Пуассона является предельным для биномиального распределения, когда n ® ¥ (n велико), а l = np остаётся постоянным (p мало). Говорят, что случайная величина X имеет распределение Пуассона с параметром l > 0, если
Pn(k) = Cnkpk(1 – p)n–k » ![]() =
= ![]() , k = 0, 1, 2, ….
, k = 0, 1, 2, ….
Вычисление математического ожидания и дисперсии дают следующие результаты:
М(X) = l; D(X) = l; s(X) = ![]() .
.
Ряд распределения имеет следующий вид:
|
X |
0 |
1 |
2 |
… |
m |
… |
|
P |
e – l |
l e – l |
|
… |
|
… |
Числовые характеристики непрерывной случайной величины.
Вспомним, что дискретная случайная величина может быть задана перечнем всех ее возможных значений и их вероятностей. Такой способ задания не является общим: он не применим, например, для непрерывных случайных величин. С этой целью вводят функцию распределения вероятностей случайной величины.
Определение 1. Функцией распределения называют функция F(x), определяющую вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х, т. е.
F(x) = P(X < x).
Геометрически это равенство можно истолковать так: F(x) есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х.
Замечание. Для дискретной случайной величины
F(x) = P(X < x) = P(![]() ) =
) = 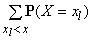 =
= ![]() .
.
Ясно, что функция F(x) однозначно определяет все вероятности pl. Поэтому функция распределения является другой формой закона распределения, иногда функцию распределения называют интегральной функцией распределения.
Свойства функции распределения
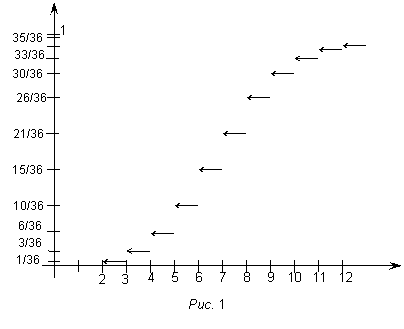
1. Значения функции распределения принадлежат промежутку [0, 1]: 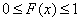 ;
; 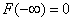 ,
, ![]() .
.
2. Если x1 < x2, то F(x1) ≤ F(x2), т. е. F(x) – неубывающая функция.
3. Для любых a < b выполняется равенство P(a ≤ X < b) = F(b) – F(a).
Пример 1. Функция распределения величины X, равной числу выпавших очков после двух бросков игральной кости (пример 4), имеет вид, показанный на рис.1.
Определение 2. Плотностью распределения вероятностей непрерывной случайной величины Х называют функцию ![]() .
.
Следовательно, F(x) = 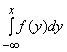 для каждого x Î( –∞, ∞).
для каждого x Î( –∞, ∞).
В случае существования плотности эту формулу, учитывая свойства интеграла, можно записать следующим образом:
P(a ≤ X < b) =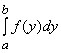 .
.
Свойства плотности распределения:
1) f(x) ![]() 0;
0;
2) 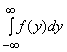 = 1;
= 1;
Пример 2. Задана плотность вероятности случайной величины Х
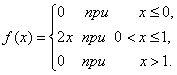
Найти вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (0,5; 1).
Решение. Искомая вероятность 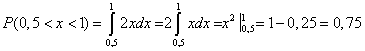 .
.
Определение 3. Математическим ожиданием случайной величины X, значения которой принадлежат интервалу (a, b), с плотностью распределения f(x) называется число
М(X) = 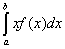 .
.
Говорят, что математическое ожидание у случайной величины X существует, если у неё конечен абсолютный момент М(|X|) = 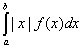 .
.
Замечание. Если X – случайная величина с плотностью распределения f(x) и g(x) – непрерывная функция, то математическое ожидание случайной величины g(X) равно
М(g(X)) = 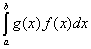 .
.
Определение 4. Дисперсией случайной величины X, значения которой принадлежат интервалу (a, b), с плотностью распределения f(x) называется число
D(X) = 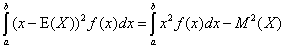 .
.
Справедливы все свойства математического ожидания и дисперсии, сформулированные для дискретных величин.
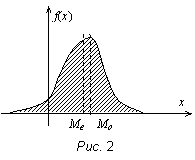 Определение 5. Средним квадратическим отклонением непрерывной случайной величины называют квадратный корень из дисперсии: s(X) =
Определение 5. Средним квадратическим отклонением непрерывной случайной величины называют квадратный корень из дисперсии: s(X) = 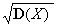 .
.
Определение 6. Модой Mо(X) непрерывной случайной величины является то её значение, в котором плотность вероятности максимальна. Медианой Mе(X) непрерывной случайной величины называется абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам (рис. 2).
Законы распределения непрерывной случайной величины
Говорят, что случайная величина Х распределена по равномерному закону на отрезке [a, b], если ее плотность имеет вид:
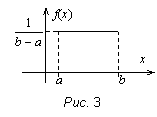 f(x) = F ¢(x) =
f(x) = F ¢(x) = 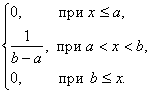
Её математическое ожидание и дисперсия имеют следующие значения
М(X) = 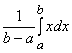 =
= ![]() , D(X) =
, D(X) = 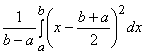 =
= ![]() .
.
Пример 1. Каждый день с 15.00 до 15.30 молодой человек стоит у книжного киоска и ожидает свою Незнакомку, которая каждый раз проходит мимо не ранее 15.20, не замечая его. Каково среднее время её появления в период его ожидания?
Решение. Незнакомка появляется в промежуток от 15.20 до 15.30 – это равномерная случайная величина. Среднее время появление характеризуется математическим ожиданием:
М(X) = ![]() = (15.20 + 15.30)/2 = 15.25. Поскольку D(X) = 102/12 = 8 мин. 20 сек., то среднее квадратическое отклонение » 2 мин. 53 сек.
= (15.20 + 15.30)/2 = 15.25. Поскольку D(X) = 102/12 = 8 мин. 20 сек., то среднее квадратическое отклонение » 2 мин. 53 сек.
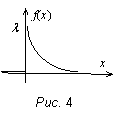 Говорят, что случайная величина Х распределена по показательному закону на отрезке [a, b], если ее плотность имеет вид:
Говорят, что случайная величина Х распределена по показательному закону на отрезке [a, b], если ее плотность имеет вид:
f(x) = 
Здесь l – постоянная положительная величина, называемая параметром показательного распределения.
Математическое ожидание и дисперсия имеют следующие значения
М(X) = 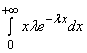 =
= ![]() ; D(X) =
; D(X) = 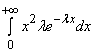 – М2(X) =
– М2(X) = ![]() ; s(X) =
; s(X) = 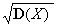 =
= ![]() .
.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 |




