Итак, получили следующее правило интегрирования:
Таким образом, если 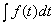 = F(t) + C, то
= F(t) + C, то 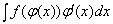 = F(j(x)) + C. Это можно записать следующим образом:
= F(j(x)) + C. Это можно записать следующим образом: ![]() =
= ![]() = F(j(x)) + C, т. е. сначала сделали замену j(x) = t, затем нашли первообразную как функцию от t и вернулись к старой переменной x заменой t = j(x).
= F(j(x)) + C, т. е. сначала сделали замену j(x) = t, затем нашли первообразную как функцию от t и вернулись к старой переменной x заменой t = j(x).
Пример 1. Рассмотрим 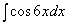 . Сделаем замену t = 6x, откуда dt = 6dx, и, следовательно, dx = (1/6)dt. Подставляем в интеграл:
. Сделаем замену t = 6x, откуда dt = 6dx, и, следовательно, dx = (1/6)dt. Подставляем в интеграл:
![]() .
.
Пример 2. Рассмотрим 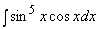 . Сделаем замену u = sinx, тогда du = cosxdx, откуда получаем
. Сделаем замену u = sinx, тогда du = cosxdx, откуда получаем 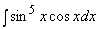 =
= ![]() =
= ![]() u6 + C =
u6 + C = ![]() sin6x + C.
sin6x + C.
2. Интегрирование по частям
Пусть u и v – дифференцируемые функции от x. Как известно, производная произведения равна (uv)¢ = u¢v + uv¢. Отсюда следует аналогичная формула для дифференциалов:
d(uv) = vdu + udv
или
udv = d(uv) – vdu.
Проинтегрировав обе части, с учётом того, что 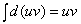 , получим:
, получим:
Эта формула называется формулой интегрирования по частям. При её применении подынтегральное выражение разбивается на два сомножителя u и dv. Эту формулу следует применять тогда, когда интеграл ![]() окажется более легким для вычисления, чем исходный интеграл
окажется более легким для вычисления, чем исходный интеграл ![]() .
.
Пример 3. Рассмотрим 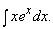 Пусть u = x, dv = exdx. Тогда du = dx, v =
Пусть u = x, dv = exdx. Тогда du = dx, v = ![]() = ex. Постоянную C здесь опускаем. Итак,
= ex. Постоянную C здесь опускаем. Итак,
Пример 4. Рассмотрим 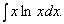 Пусть u =lnx, dv = xdx. Тогда du=
Пусть u =lnx, dv = xdx. Тогда du=![]() , v=
, v=![]() =
= ![]() .
.
Определённый интеграл
Пусть y = f(x) – производительность труда, являющаяся непрерывной функцией на временном интервале (a, b) (рис.1). Как найти объём проделанной работы?
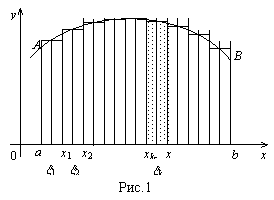 Разобьём отрезок [a, b] точками a = x0 < x1 < x2 < … < xn – 1 < xn = b на n элементарных отрезков, длины которых обозначим через Dxk (k = 1, 2, 3, …, n), т. е. Dxk = xk – xk – 1. В каждом из элементарных отрезков [xk – 1, xk] выберем произвольную точку xk. Значение функции в этой точке f(xk) умножим на длину отрезка Dxk, получим произведение f(xk)×Dxk, приближённо равное проделанной работе за период от xk – 1 до xk. Причём приближение будет тем точнее, чем меньше интервал Dxk = xk – xk – 1. Произведение f(xk)×Dxk выражает площадь прямоугольника с основанием Dxk и высотой f(xk) (на рисунке он заштрихован). Составим сумму всех таких произведений:
Разобьём отрезок [a, b] точками a = x0 < x1 < x2 < … < xn – 1 < xn = b на n элементарных отрезков, длины которых обозначим через Dxk (k = 1, 2, 3, …, n), т. е. Dxk = xk – xk – 1. В каждом из элементарных отрезков [xk – 1, xk] выберем произвольную точку xk. Значение функции в этой точке f(xk) умножим на длину отрезка Dxk, получим произведение f(xk)×Dxk, приближённо равное проделанной работе за период от xk – 1 до xk. Причём приближение будет тем точнее, чем меньше интервал Dxk = xk – xk – 1. Произведение f(xk)×Dxk выражает площадь прямоугольника с основанием Dxk и высотой f(xk) (на рисунке он заштрихован). Составим сумму всех таких произведений:
Sn = ![]() .
.
Эта сумма называется интегральной суммой для функции y = f(x) на отрезке [a, b]. Эта величина выражает площадь ступенчатой фигуры, состоящей из прямоугольников, и приближённо равна проделанной работе за период от a до b.
В то же время данная площадь приближённо равна площади криволинейной трапеции aABb, которая представляет собой фигуру, ограниченную сверху графиком функции y = f(x), снизу – осью Ox, с боков – прямыми x = a и x = b. Погрешность этого равенства при безграничном убывании всех Dxk стремится к нулю.
Обозначим через l длину наибольшего из элементарных отрезков [xk – 1, xk], т. е. l = maxDxk (k = 1, 2, 3, …, n). Тогда точное значение площади криволинейной трапеции S получится как предел:
S = ![]() .
.
Этот предел и называется определённым интегралом.
Определённый интеграл обозначается символом 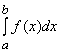 («определённый интеграл в пределах от a до b»). f(x) называется подынтегральной функцией; x – переменной интегрирования; a – нижним пределом интегрирования; b – верхним пределом интегрирования.
(«определённый интеграл в пределах от a до b»). f(x) называется подынтегральной функцией; x – переменной интегрирования; a – нижним пределом интегрирования; b – верхним пределом интегрирования.
Итак,
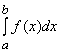 =
= ![]() .
.
Геометрический смысл определённого интеграла состоит в том, что определённый интеграл в пределах от a до b равен площади криволинейной трапеции, ограниченной графиком неотрицательной функции y = f(x), осью Ox и прямыми x = a и x = b.
Свойства определённого интеграла
|
1. 2. 3. При любом расположении точек a, b, c: |
4. 5. Свойства 4 и 5 означают линейность определённого интеграла. |
Вычисление определённого интеграла для непрерывных функций осуществляется по формуле Ньютона-Лейбница:
где F(x) – первообразная для f(x).
Пример. ![]() =
=![]()
![]() =
= ![]() .
.
Методы вычисления определённого интеграла
Замена переменных в определённом интеграле делается аналогично такой замене в неопределённом интеграле. В отличие от неопределённого интеграла в данном случае нет необходимости возвращаться к исходной переменной интегрирования. Достаточно лишь найти пределы интегрирования по новой переменной, предварительно выразив новую переменную через старую.
Пример 1. Вычислить интеграл 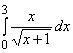 .
.
Решение. Пусть u = ![]() , тогда x = u2–1, dx = 2udu. Если x = 0, то u = 1; если x = 3, то u = 2.
, тогда x = u2–1, dx = 2udu. Если x = 0, то u = 1; если x = 3, то u = 2.
Получаем
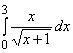 =
= 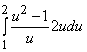 =
= 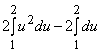 =
= ![]() u3
u3![]() – 2u
– 2u![]() =
= ![]() (8 – 1) – 2(2 – 1) =
(8 – 1) – 2(2 – 1) = ![]() .
.
Интегрирование по частям получит вид: 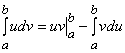 .
.
Пример 2. Вычислить интеграл 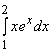 .
.
Решение. Пусть u = x, dv = exdx, тогда v = ![]() = ex. Получаем
= ex. Получаем 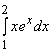 =
= 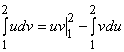 = xex
= xex![]() –
– ![]() = 2e2 – e – ex
= 2e2 – e – ex![]() = e2.
= e2.
Несобственный интеграл
Несобственными интегралами называются: 1) интегралы с бесконечными пределами; 2) интегралы от неограниченных функций. Вычисление их происходит точно так же, как и обычных интегралов, но с заменой ¥, например, буквой A с последующим предельным переходом при A ® ¥.
Пример 1. ![]() =
= 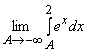 =
= 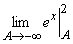 =
= ![]() = e2.
= e2.
Пример 2. ![]() =
= 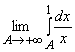 =
= 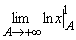 =
= ![]() – не существует.
– не существует.
Если этот предел не существует, то несобственный интеграл называется расходящимся; если же предел существует и конечен – сходящимся.
Дифференциальные уравнения
Определение 1. Обыкновенным дифференциальным уравнением называется уравнение, связывающее независимую переменную x, искомую функцию y = f(x) и её производные y¢, y¢¢, …, y(n). Наивысший порядок производной, входящей в уравнение, называется порядком дифференциального уравнения.
Например, xy¢ = 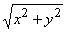 + y – обыкновенное дифференциальное уравнение первого порядка;
+ y – обыкновенное дифференциальное уравнение первого порядка;
![]() +5
+5![]() +6y = 0 – обыкновенное дифференциальное уравнение второго порядка;
+6y = 0 – обыкновенное дифференциальное уравнение второго порядка;
y¢¢¢ + 5y¢¢× y2 = 0 – обыкновенное дифференциальное уравнение третьего порядка.
Обыкновенное дифференциальное уравнение n-го порядка в общем виде можно записать так:
F(x, y¢, y¢¢, …, y(n)) = 0, (1)
где x – независимая переменная; y = y(х) – искомая функция переменной x; y¢, y¢¢, …, y(n) – её производные; F – заданная функция своих аргументов. Функция F может не содержать некоторых своих аргументов, но непременно должна зависеть от y(n) (если речь идёт об уравнении n-го порядка).
Определение 2. Функция y = j(x), определённая и непрерывно дифференцируемая n раз в интервале (a, b), называется решением дифференциального уравнения (1) на этом интервале, если она обращает указанное уравнение в тождество, т. е.
F(x, j¢(x), j¢¢(x), j¢¢¢(x), …, j (n)(x)) º 0
для всех x Î (a, b).
График решения дифференциального уравнения n-го порядка называется интегральной кривой.
Задача Коши для дифференциального уравнения n-го порядка состоит в следующем: найти решение y = y(x) уравнения (1), удовлетворяющее условиям:
y(x0) = y0, y¢(x0) = y0¢, y¢¢(x0) = y0¢¢, y¢¢¢(x0) = y0¢¢¢, …, y(n – 1)(x0) = y0(n –
Общим решением дифференциального уравнения n-го порядка (1) называется функция
y = j(x, C1, C2, C3, … , Cn), (3)
зависящая от x и n произвольных постоянных C1, C2, C3,…, Cn и обладающая следующими свойствами:
1) при любых значениях произвольных постоянных C1, C2, C3,…, Cn она обращает уравнение (1) в тождество;
2) значения постоянных C1, C2, C3,…, Cn можно подобрать так, чтобы она удовлетворяла условиям (2).
Частным решением дифференциального уравнения n-го порядка называется решение, получающееся из общего решения (1) при фиксированных значениях произвольных постоянных, т. е.
y = j(x, C10, C20, C30, … , Cn0),
где C10, C20, C30, … , Cn0 – некоторые числа.
Определение 3. Если дифференциальное уравнение имеет вид
j(y)dy = f(x)dx (4)
или может быть приведено к такому виду, оно называется уравнением с разделяющимися переменными.
Выражение (4) можно рассматривать как равенство двух дифференциалов, а неопределённые интегралы от них будут отличаться постоянным слагаемым. Интегрируя левую часть по y, а правую по x, получим:
Вычислим эти интегралы, мы и получим общее решение уравнения (4).
Пример 1. Найти зависимость численности y народонаселения от времени t, если численность y и скорость её изменения y¢ связаны дифференциальным уравнением: y¢ = 2y. Определить зависимость скорости и ускорения изменения численности от времени.
Решение. Перепишем ![]() = 2y, можем перенести одну переменную влево, другую – вправо
= 2y, можем перенести одну переменную влево, другую – вправо ![]() = 2t, интегрируем обе части:
= 2t, интегрируем обе части: ![]() =
=![]() . Откуда lny = 2t+C, или y = e2t+C = eCe2t. Положим C1 = eC, тогда общее решение запишется в виде y = C1e2t; оно представляет собой множество экспонент. Найдём скорость и ускорение изменения численности: y¢ = 2C1e2t, y¢¢ = 4C1e2t.
. Откуда lny = 2t+C, или y = e2t+C = eCe2t. Положим C1 = eC, тогда общее решение запишется в виде y = C1e2t; оно представляет собой множество экспонент. Найдём скорость и ускорение изменения численности: y¢ = 2C1e2t, y¢¢ = 4C1e2t.
Пример 2. Решить уравнение x(y2 - 4)dx + ydy = 0.
Решение. Разделив обе части уравнения на y2 – 4 ![]() 0, имеем
0, имеем 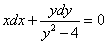 . Интегрируя, находим x2 + ln|y2 – 4| = ln|C|, или y2 – 4 = С
. Интегрируя, находим x2 + ln|y2 – 4| = ln|C|, или y2 – 4 = С ![]() . Это общее решение данного дифференциального уравнения.
. Это общее решение данного дифференциального уравнения.
Пусть теперь y2 – 4 = 0, т. е. у = ![]() 2. Непосредственной подстановкой убеждаемся, что у =
2. Непосредственной подстановкой убеждаемся, что у = ![]() 2 – решение исходного уравнения. Но оно не будет особым решением, т. к. его можно получить из общего решения при С = 0.
2 – решение исходного уравнения. Но оно не будет особым решением, т. к. его можно получить из общего решения при С = 0.
Пример 3. Решить уравнение y¢ = ![]() , удовлетворяющее следующему начальному условию: y(2) = 1, т. е. y0 = 1 при x0 = 2.
, удовлетворяющее следующему начальному условию: y(2) = 1, т. е. y0 = 1 при x0 = 2.
Решение. Перепишем 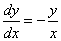 или
или ![]() . Проинтегрировав последнее равенство, получим lny = -lnx + lnC = ln
. Проинтегрировав последнее равенство, получим lny = -lnx + lnC = ln![]() ↔ y =
↔ y = ![]() это семейство функций является общим решением, где C – произвольная постоянная.
это семейство функций является общим решением, где C – произвольная постоянная.
Найдём частное решение. Подставляя значения x0 и y0 в формулу общего решения y = ![]() , получим 1 =
, получим 1 = ![]() , откуда C = 2. Следовательно, искомым частным решением будет функция y =
, откуда C = 2. Следовательно, искомым частным решением будет функция y = ![]() .
.
Определение 4. Линейным дифференциальным уравнением первого порядка называется уравнение вида
a(x)y¢ + b(x)y = c(x).
Здесь y = y(x) – искомая функция; a(x), b(x), c(x) – заданные функции.
Предполагая, что данные функции непрерывны и a(x) ¹ 0, последнее уравнение можно преобразовать к следующему виду:
y¢ + p(x)y = f(x). (5)
Решение уравнения (5) будем искать в виде произведения двух функций от x:
y = u(x)v(x). (6)
Так как y¢ = u¢v + uv¢, то (5) примет вид u¢v + uv¢ + p(x)uv = f(x) или
u¢v + u(v¢ + p(x)v) = f(x). (7)
Выберем функцию v такой, чтобы v¢ + p(x)v = 0 – это уравнение с разделяющими переменными. Найдём какое-нибудь его решение:
![]() = – p(x)dx Þ ln|v| = –
= – p(x)dx Þ ln|v| = – ![]() + C, положим C = 0, тогда v =
+ C, положим C = 0, тогда v = 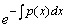 .
.
Учитывая, что v¢ + p(x)v = 0, уравнение (7) примет вид u¢v = f(x) – уравнение с разделяющими переменными.
du = ![]() Þ u =
Þ u = 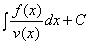 ,
,
Подставляя v и u в (6) получим общее решение (5): y = v(x)× ![]() .
.
Пример 4. Решить уравнение y¢ + y cosx = e – sinx .
Решение. p(x) = cosx, f(x) = e –sinx.
Откуда v =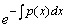 = e–sinx , u =
= e–sinx , u =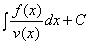 = x + C. Общее решение: y = uv = (x + C)e–sinx .
= x + C. Общее решение: y = uv = (x + C)e–sinx .
Определение 5. Дифференциальное уравнение
y¢¢ + py¢ + qy = 0, (8)
где p и q – постоянные числа, называется линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами.
Будем искать решение в виде
y = e kx (k = const). (9)
Подставляя эту функцию и её производные y¢ = ke kx, y¢¢ = k2e kx в уравнение (8), получим тождество k2e kx + pke kx + qe kx º 0, или e kx(k2 + pk + q) º 0. Следовательно, функция (9) будет решением (8) тогда и только тогда, когда k2 + pk + q = 0, т. е. когда k – корень алгебраического уравнения. Это уравнение называется характеристическим уравнением.
Если оно имеет различные действительные корни k1, k2 (k1 ¹ k2), то общее решение уравнения (8) определяется формулой y0 = C1![]() + C2
+ C2![]() .
.
В случае кратного корня характеристического уравнения k1 = k2 = k общее решение уравнения (8) выражается формулой y0 = (C1 + C2x)e kx.
Если характеристическое уравнение имеет комплексно-сопряжённые корни k1 = a – ib, k2 = a + ib (где i2 = –1), то y0 = (C1cosbx + C2sinbx)![]() .
.
Элементы комбинаторики
Комбинаторика изучает вопросы о том, сколько различных комбинаций, подчинённых тем или иным условиям, можно составить из заданных объектов. В этом пункте мы будем рассматривать конечные множества, обозначая их фигурными скобками. Например, {a, b, c} или {1, 2, 3, 4, 5}. Порядок элементов в такой записи не имеет значения, и два множества равны, если они состоят из одних и тех же элементов. Поскольку природа объектов нас не интересует, а интересуют их комбинации, то всегда можно перейти к конечным подмножествам натуральных чисел. Конечные множества также будем называть наборами.
Конечные множества называются упорядоченными, если при их сравнении учитывают не только состав элементов, но и порядок расположения их элементов. Мы будем рассматривать линейно упорядоченные множества, обозначая их круглыми скобками. Например, (a, b, c) ≠ (b, c, a). Два упорядоченных множества равны, если они состоят из одних и тех же элементов, расположенных в одном и том же порядке.
Определение 1. Упорядоченные множества, составленные из всех элементов данного конечного множества, называются перестановками этого множества.
Пример 1. Множество из трёх элементов {1, 2, 3} имеет следующие перестановки: (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 2, 1), (3, 1, 2).
Число всех перестановок множества из n элементов обозначим Pn.
Теорема 1 (о числе перестановок). Число перестановок множества из n элементов определяется по формуле Pn =n!, где n!= 1∙2∙3∙…∙n.
Пример 2. Цифры 0, 1, 2, 3 написаны на четырёх карточках. Сколько различных четырёхзначных чисел можно составить из этих карточек?
Решение. Число различных комбинаций из четырёх цифр равно 4!. Из них нужно исключить те комбинации, которые начинаются с нуля, т. е. 3!. В результате число различных четырёхзначных чисел равно 4!–3!=18.
Определение 2. Упорядоченные наборы, состоящие из k различных элементов, выбранных из данных n элементов, называются размещениями из n элементов по k.
Размещения могут отличаться друг от друга как элементами, так и порядком.
Пример 3. Различными размещениями из трех элементов {1, 2, 3} по два будут наборы (1, 2), (2, 1), (1, 3), (3, 1), (2, 3), (3, 2).
Число всех размещений из n элементов по k обозначается ![]() . При k = n число размещений совпадает с числом перестановок.
. При k = n число размещений совпадает с числом перестановок.
Теорема 2 (о числе размещений). Число размещений из n элементов по k определяется по формуле
![]() = n(n– 1)…(n– k +1) =
= n(n– 1)…(n– k +1) = 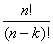 .
.
Пример 4. Студентам надо сдать 4 экзамена за 8 дней. Сколькими способами можно составить расписание сдачи экзаменов?
Решение. Занумеруем дни сдачи экзаменов 1, 2, 3, … 8. Составлять расписания можно следующим образом. С начала выберем дни для сдачи экзаменов, например, (2, 4, 5, 7), а затем порядок сдачи экзаменов. Таких наборов ![]() = 8∙7∙6∙5 = 1680.
= 8∙7∙6∙5 = 1680.
Определение 3. Неупорядоченные наборы, состоящие из k различных элементов, выбранных из данных n элементов, называются сочетаниями из n элементов по k.
Сочетания отличаются друг от друга только элементами.
Пример 5. Для множества {1, 2, 3} сочетаниями по 2 являются {1, 2}, {1, 3}, {2, 3}.
Число всех сочетаний из n элементов по k обозначается ![]() .
.
Теорема 3 (о числе сочетаний). Число сочетаний из n элементов по k определяется по формуле
![]() =
= 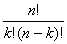 .
.
Пример 6. В хоккейном турнире участвуют 6 команд. Каждая команда должна сыграть с каждой одну игру. Сколько игр сыграно в турнире?
Решение. Различные пары команд образуют сочетания из 6 по 2, поскольку порядок среди двух команд, играющих в одной игре, безразличен. Следовательно, число игр ![]() = =
= =![]() =15.
=15.
Теорема 4 (о числе комбинаций или правило умножения). Число различных комбинаций элементов вида (a1, a2, …, ar), где al – некоторый элемент l-той группы, состоящей из nl элементов, равно n1n2…nr.
Пример 7. Из трёх классов спортивной школы нужно составить команду для соревнований, взяв по одному ученику от класса. Сколько различных команд можно составить, если в одном классе учатся 18, в другом – 20, а в третьем – 22 ученика?
Решение очевидно: 18∙20∙22 = 7920.
Случайные события. Основные определения.
Эксперимент (опыт или испытание) считается случайным, если он может закончиться любым из совокупности известных результатов, но до осуществления эксперимента нельзя предсказать, каким именно. Различные результаты эксперимента мы будем называть исходами (случаями или шансами). Причем в дальнейшем под термином “исход” будем подразумевать только взаимно исключающие исходы, т. е. те, которые не могут наступить одновременно.
Определение 1. Множество всех взаимно исключающих исходов эксперимента называется пространством элементарных событий (схемой случаев или схемой урн).
Таким образом, термины “элементарное событие” и “исход” будут считаться синонимами. Пространство элементарных событий обозначим буквой W, а его исходы – буквой w с различными индексами и без них или другими понятными из контекста символами.
Определение 2. Произвольное подмножество пространства элементарных событий называется событием.
Событие может состоять из одного или нескольких элементарных событий, а также состоять из счётного или несчётного числа элементарных событий.
События будем обозначать заглавными латинскими или русскими буквами A, B, C, …, Г, Р, Ч, …, или записывать словами, например, {выпало четное число очков на игральной кости}. Говорят, что событие A наступило, если эксперимент заканчивается одним из исходов, входящих в событие A.
Определение 3. Достоверным называют событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий.
Невозможным называется событие, которое заведомо не произойдет, если будет осуществлена определенная совокупность условий.
Определение 4. Случайным называется событие, которое при осуществлении совокупности условий может либо произойти, либо не произойти.
Определение 5. События называются несовместными, ели появление одного из них исключает появление других событий в одном и том же испытании.
События называют единственно возможными, если появление в результате испытания одного и только одного из них является достоверным событием.
События называют равновозможными, если имеются основания считать, что ни одно из этих событий не является более возможными, чем другие.
Примеры:
1) Бросание монеты.
Пространство элементарных событий состоит из двух исходов: Г = {выпал герб}, Р = {выпала решетка}, т. е. W = {Г, Р}.
2) Бросание игральной кости (кубика).
Пространство элементарных событий W = {1, 2, 3, 4, 5, 6}. Событие Ч = {выпало чётное число} состоит из трёх исходов, т. е. Ч = {2, 4, 6}. Событие {выпало число больше шести}= Æ.
В зависимости от задачи в одном и том же эксперименте можно по-разному выбирать пространство элементарных событий. Рассмотрим при бросании игральной кости, если нас интересует лишь то, что выпало чётное или нечётное число, можно считать W = {Ч, Н}, где Ч = {чётное число}, Н = {нечётное число}.
Пример неправильно выбранного пространства элементарных событий. Пусть при бросании игральной кости Ч = {чётное число очков}, Т = {число очков, кратное трём}. Тогда W = {Ч, Т, 1, 5} составляет все исходы эксперимента, однако исходы Ч и Т могут наступать одновременно. Ситуацию легко исправить, например, если Т заменить 3.
Определение 6. Операции алгебры множеств имеют следующую интерпретацию на языке случайных событий:
1) Суммой двух событий A и B (обозначается A+B) называется событие, состоящее в появлении хотя бы одного из этих событий.
2) Произведением двух событий A и B (обозначается AB) называется событие, состоящее в совместном появлении этих событий.
3) Разность двух событий A и B (обозначается A–B) называется событие, состоящее в появлении события A, но при этом не наступает событие B.
4) Противоположным (дополнительным) для события A (обозначается ![]() ) называется событие, состоящее в том, что событие A не наступило.
) называется событие, состоящее в том, что событие A не наступило.
5) Говорят, что событие A содержится в событии B (обозначается A Ì B), если наступление события A обязательно влечёт наступление события B.
Свойства операций над событиями
1) A+B = B+A; 2) AB = BA; 3) AW = A; 4) ABÌ A; 5) A+![]() = W; 6) A
= W; 6) A![]() = Æ; 7)
= Æ; 7) ![]() = A;
= A;
8) A–B = A ; 9) (A ![]() B)C = AC
B)C = AC ![]() BC; 10)
BC; 10) ![]() =
= ![]() ; 11)
; 11) ![]() =
= ![]() + .
+ .
Эти свойства являются другой записью соответствующих свойств операций алгебры множеств и доказываются аналогично.
Следующие свойства являются следствиями свойств 9), 10) и 11):
9¢) 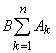 =
= 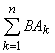 ; 10¢)
; 10¢) ![]() =
= ![]() ; 11¢)
; 11¢) ![]() =
= ![]() .
.
Эти равенства верны и для n = ¥.
Пример 1. Двое играют в шахматы. Событие A означает, что выиграл первый игрок, событие B – что выиграл второй игрок. Что означают события
а) ; б) ![]() + ; в) –A; г)
+ ; в) –A; г) ![]() –B?
–B?
Решение. W = {A, B, C}, где C – сыграли вничью.
Тогда = {A, C}, ![]() ∆B=C,
∆B=C, ![]() + = W, –A = C,
+ = W, –A = C, ![]() –B = C.
–B = C.
Получаем ответы:
а) первый игрок выиграл или сыграл вничью;
б) возможен любой исход;
в) партия закончилась вничью;
г) партия закончилась вничью.
Классическое определение вероятности
Вероятность – одно из основных понятий теории вероятности. Существует несколько определений этого понятия. Приведем определение, которое называют классическим.
Рассмотрим пример. Пусть в урне содержится 6 одинаковых шаров, причем 2 из них – красные, 3 – синих, 1 – белый. Очевидно, возможность вынуть наудачу из урны цветной (т. е. синий или красный) шар больше, чем возможность извлечь белый шар. Можно ли охарактеризовать эту возможность числом? Оказывается, можно. Это число и называют вероятностью события (появления цветного шара). Таким образом, вероятность есть число, характеризующее степень возможности появления события.
Поставим перед собой задачу дать количественную оценку возможности того, что взятый наудачу шар цветной. Появление цветного шара будем рассматривать в качестве события А. Каждый из возможных результатов испытания (испытание состоит в извлечении шара из урны) назовем элементарным исходом (элементарным событием). Элементарные события обозначим через w1, w2, w3 и т. д. В нашем примере возможны следующие 6 элементарных исходов: w1 - появился белый шар, w2, w3 - появился красный шар, w4, w5, w6 - появился синий шар. Легко видеть, что эти исходы образуют полную группу попарно несовместных событий (обязательно появиться только один шар) и они равновозможны (шар вынимают наудачу, шары одинаковы и тщательно перемешаны).
Те элементарные исходы, в которых интересующее нас событие наступает, назовем благоприятствующими этому событию. В нашем примере благоприятствуют событию А (появлению цветного шара) следующие 5 исходов: w2, w3, w4, w5, w6. Таким образом, событие А наблюдается, если в испытании наступает один, безразлично какой, из элементарных исходов, благоприятствующих А. В этом смысле событие А подразделяется на несколько элементарных событий (w2, w3, w4, w5, w6); элементарное же событие не подразделяется на другие события.
Отношение числа благоприятствующих событию А элементарных исходов к их общему числу называют вероятностью события А и обозначают Р(А). В рассматриваемом примере всего элементарных исходов 6; из них 5 благоприятствуют событию А. Следовательно, вероятность того, что взятый шар окажется цветным, равна Р(А) = 5/6. Это число и дает ту количественную оценку степени возможности появления цветного шара, которую мы хотели найти. Дадим теперь определение вероятности.
Определение. Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу. Итак, вероятность события А определяется формулой Р(А) = m/n, где m – число элементарных исходов, благоприятствующих А, n - число всех всевозможных элементарных исходов испытания.
Вероятность события удовлетворяет следующим требованиям: а) вероятность события выражается долей от целого, т. е. является числом от нуля до единицы; б) вероятность наступления достоверного события принимается равной единице; в) вероятность невозможного события считают равным нулю; г) вероятность суммы попарно несовместных событий равна сумме вероятностей каждого из событий.
Примеры.
1) При бросании правильной монеты P(Г) = P(Р) = ½.
2) При бросании игральной кости P(1) = …= P(6) = 1/6. P(выпало чётное число) = 3/6 = ½.
Пример 1. Какова вероятность угадать (выиграть) в лотерее 6 чисел из 49?
Решение. В этой задаче W – совокупность всех сочетаний из 49 чисел по 6, следовательно, n = ![]() – количество различных вариантов заполнения карточки. Благоприятный выигрышу только один, поэтому P(угадать 6 из 49) = 1/
– количество различных вариантов заполнения карточки. Благоприятный выигрышу только один, поэтому P(угадать 6 из 49) = 1/![]() =1/ ≈ 1/14 000 000.
=1/ ≈ 1/14 000 000.
Замечание. Абстрактная теория занимается в основном разработкой правил пересчёта одних вероятностей в другие, предполагая, что исходные вероятности даны и не нуждаются ни в каких обоснованиях их действительных численных значений. В частности, в экспериментах с равновозможными исходами значения вероятностей известны априори. А вывод о том, какие исходы считать равновозможными, основан чаще всего на соображениях, связанных с симметрией и однородностью. Например, если монета симметрична и сделана из однородного материала, то шансы выпадения герба и решётки совпадают, т. е. вероятности равны ½.
Выяснению численных значений вероятностей в различных конкретных экспериментах посвящена другая математическая дисциплина – статистика.
Свойства вероятностей:
1) P(W) = 1 (достоверное событие);
2) P(Æ) = 0 (невозможное событие);
3) Если AÌ B, то P(A)≤P(B);
4) 0 ≤ P(A) ≤ 1;
5) P(![]() ) = 1 – P(A);
) = 1 – P(A);
6) P(A+B) = P(A) + P(B) – P(AB).
Следствие 1. Если AB = Æ, т. е. события A и B несовместны, то P(A+B) = P(A) + P(B).
Следствие 2. Если C Ì D, то P(D – C) = P(D) – P(C).
Геометрические вероятности
Пусть в пространстве задана некоторая область. Пусть результатом эксперимента является случайный выбор точки из этой области. Выбор любой точки области равновозможен. Найдем вероятность попадания точки в область.
Заданную область обозначим W. Символом mes обозначим меру Лебега данной области: для прямой это длина, для плоскости – площадь, для трёхмерного пространства – объём. Будем говорить, что событие AÌW наступило, если случайно выбранная точка принадлежит множеству A.
Определение. Вероятности называются геометрическими, если для любого события AÌW вероятность этого события заданна формулой
P(A) = ![]() .
.
Свойства геометрических вероятностей точно такие же, как и для вероятностей в классическом определении.
Пример 1. На плоскости начерчены 2 концентрические окружности, радиусы которых 5 и 10 см соответственно. Найти вероятность того, что точка, брошенная наудачу в большой круг, попадет в кольцо, образованное построенными окружностями. Предполагается, что вероятность попадания точки в плоскую фигуру пропорциональна площади этой фигуры и не зависит от ее расположения.
Решение. Площадь кольца Sк = π(102 – 52) = 75π. Площадь большого круга Sб = π102 = 100π. Искомая вероятность P = 75π/100π = 0,75.
Пример 2 (о встрече). Два студента условились встретиться в определенном месте между 12 и 13 часами дня. Пришедший первым ждет второго в течении 15 минут, после чего уходит. Найти вероятность того, что встреча состоится, если каждый студент наудачу выбирает момент своего прихода.
Решение. Пусть x – время прихода первого студента, а y – второго. Тогда (x, y) Î[0, T]´ [0, T] º W. Поскольку они приходят случайным образом, то все исходы равновозможные. Событие A = {они встретятся} можно задать так: A = {(x, y)Î[0, T]´ [0, T] : |y – x| ≤ 15}. Множество A образует те точки квадрата, которые лежат между прямыми y = x – 15 и y = x + 15. Поэтому mesA = 602 – Поскольку mesW = 602, то

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 |




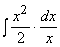 = lnx
= lnx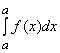
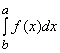 .
.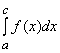 +
+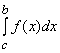 .
.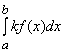
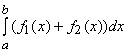
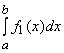 +
+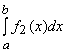 .
.