Математика и информатика (стр. 4 )

Пример 2. Какова вероятность обслуживания в ближайшие полчаса с учётом того, что поток обслуженных клиентов имеет плотность 4 человека в час? Каково среднее время обслуживания?

Решение. P(0 £ X £ 0.5) = 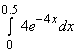= –= 1 – e –2 » 0.864665. Среднее время М(X) = = четверть часа.

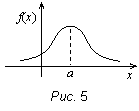Говорят, что случайная величина Х распределена по нормальному закону на отрезке [a, b], если ее плотность имеет вид:

f(x) = .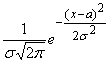

Вычисление математического ожидания и дисперсии дают следующие результаты:

М(X) = a, D(X) = s2, s(X) = 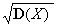= s.

Если a = 0 (центрированная случайная величина) и s = 1, то нормальное распределение с такими параметрами называется стандартным. Функция распределения в этом случае имеет вид

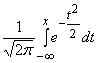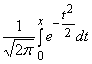F(x) = = + = + F(x),

где F(x) – функция Лапласа. С использованием функции Лапласа получаем, что вероятность попадания в заданный интервал нормальной случайной величины равна

P(a < X < b) = F() – F().

Пример 3. Пусть М(X) = 40 и D(X) = 100. Вычислить вероятность того, что в данном испытании результат будет заключён в интервале (30, 80), считая закон распределения X нормальным.

Решение. P(30 < X < 80) = F() – F() = F(4) – F(– 1) = F(4) + F(1) = 0.4999 + 0.3413 = 0.68256.

Основные определения математической статистики

Установление закономерностей, которым подчинены массовые случайные явления, основано на изучении методами теории вероятностей статистических данных – результатов наблюдений.

Первая задача математической статистики – указать способы сбора и группировки статистических сведений, полученных в результате наблюдений или в результате специально поставленных экспериментов.

Вторая задача математической статистики – разработать методы анализа статистических данных в зависимости от целей исследований. Сюда относятся:

а) оценка неизвестной вероятности события; оценка неизвестной функции распределения; оценка параметров распределения, вид которого известен; оценка зависимости случайной величины от одной или нескольких случайных величин и др.;

б) проверка статических гипотез о виде неизвестного распределения или о величине параметров распределения, вид которого известен.

Временная математическая статистика разрабатывает способы определения числа необходимых испытаний до начала исследования (планирование эксперимента), в ходе исследования (последовательный анализ) и решает многие другие задачи. Современную математическую статистику определяют как науку о принятии решений в условиях неопределенности.

Итак, задача математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов.

Допустим, целью исследования является выявление ведущих тенденций среди множества некоторых объектов. Например, вымирание каких видов животных можно ожидать в ближайшее время на территории России? Если число исследуемых объектов довольно велико, то не всегда можно провести сплошное исследование, либо это исследование очень дорогостоящее. В этом случае применяется выборочный метод. Его сущность заключается в том, что обследованию подвергаются не все объекты совокупности, а только некоторая их часть, случайно выбранная из всего множества объектов.

Определение 1. Генеральной совокупностью называется совокупность всех однородных объектов, подлежащих изучению. Выборочной совокупностью, или выборкой, называется совокупность объектов, случайно отобранных из генеральной совокупности. Объёмом совокупности (генеральной или выборочной) называется число её объектов. Например, если из 10 000 студентов института психологи тестируют 100 человек, то объём генеральной совокупности N = 10 000, а объём выборки n = 100.

При составлении выборки можно поступать двояко: после того, как объект отобран и над ним произведено наблюдение, он может быть возвращен, либо не возвращен в генеральную совокупность. В соответствии со сказанным,

Определение 2. Повторной называется выборка, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность. Бесповторной называется выборка, при которой отобранный объект в генеральную совокупность не возвращается. В психологической практике чаще используется бесповторная выборка.

Недостаток повторной выборки состоит в том, что когда объем генеральной совокупности мал, возвращение ведет к уменьшению получаемой информации, так как существует возможность выбора одного и того же результата дважды. Однако этот метод применяется чаще, ввиду того, что его легче описать математически.

В тех случаях, когда численность членов совокупности, из которой производят выборку, велика по сравнению с объемом выборки, оба метода дают почти одинаковые результаты.

Определение 3. Выборка называется репрезентативной (представительной), если по ней можно уверенно судить об интересующем нас признаке всей генеральной совокупности. Необходимым условием репрезентативности является случайный отбор.

Определение 4. Пусть в результате n испытаний получены следующие значения случайной величины, расположенные в неубывающем порядке:

x1, x2, …, xn, где x1 £ x2 £ …£ xn. (1)

Последовательность (1) наблюдаемых значений, записанных в неубывающем порядке, называется вариационным рядом, а сами эти значения xi называют вариантами (варианта).

Среди вариант могут оказаться равные, тогда результат испытаний можно представить в виде таблицы (табл. 1), где x1 £ x2 £ …£ xk, ni – (абсолютная) частота появления значения xi,

Определение 5. Относительной частотой wi варианты xi называется отношение её частоты к объёму выборки:

wi = . (2)

Очевидно, что 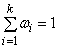сумма относительных частот всегда равна единице.

Определение 6. Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот.

Пример 1. Задано распределение частот выборки объёма n = 60 (табл. 2). Найти распределение относительных частот.

Решение. Применяя формулу (2), вычисляем относительные частоты и получаем таблицу 3.

Статическое распределение выборки может быть изображено графически – в виде полигона и гистограммы.

Определение 7. Полигоном частот называют ломанную, отрезки который соединяют точки (x1, n1), (x2, n2), …, (xk, nk).

Для построения полигона частот на оси абсцисс откладывают варианты xi, а на оси ординат – соответствующие им частоты ni. Точки (xi, ni) соединяют отрезками прямых и получают полигон частот.

Определение 8. Полигоном относительных частот называют ломанную, отрезки который соединяют точки (x1, w1), (x2, w2), …, (xk, wk).

Для построения полигона частот на оси абсцисс откладывают варианты xi, а на оси ординат – соответствующие им относительные частоты wi. Точки (xi, wi) соединяют отрезками прямых и получают полигон относительных частот.

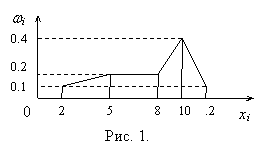
Пример 2. Рассмотрим полигон частот статистического распределения, приведённого в табл. 4 (рис. 1).

Определение 9. Гистограммой частот называется ступенчатая фигура, состоящая из прямоугольников с основанием h = xi – xi–1 и высотами ni/h.

На оси абсцисс откладывают частичные интервалы длиной h, на интервале строят прямоугольник высотой ni/h (плотность частоты). Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс, на высоте wi/h.

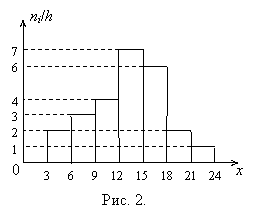
Пример 3. Приведём гистограмму частот распределения объёма n = 75, см. табл. 5, рис. 2.

Пример 4 (для самостоятельного решения). Как известно, почерк человека, в том числе наклон букв, тесно связан с его характером. Низкий наклон (30-40 град.) свидетельствует о вспыльчивости и возбудимости человека, излишней прямоте и торопливости в поступках; наклон 40-50 град. характеризует гармоническое развитие натуры; наклон 50-90 град. свидетельствует о самообладании, узком диапазоне увлечений.

Среди студентов института выборочно был исследован почерк 50 человек. Оказалось, что почерк у 30% присутствующих имеет низкий наклон, у 50% – наклон 40-50 и у 20% – наклон 50-90 град.

Найти распределение частот, относительных частот, построить полигон и гистограмму. С какой частотой встречается наклон почерка в границах от 45 до 60 град.?

Определение 10. Эмпирической функцией распределения (функцией распределения выборки) называется функция F*(x), определяющая для каждого значения x частоту события X < x.

Пусть nx – число вариант, меньших x, n – объём выборки. Тогда

F*(x) = . (3)

Из определения эмпирической функции следуют её свойства:

1.  Значения функции F*(x) принадлежат отрезку [0, 1].

2.  F*(x) – неубывающая функция.

3.  Если a – наименьшая, b – наибольшая варианта, то

F*(x) = 0 при x £ a;

F*(x) = 1 при x > b.

4.  Функция F*(x) непрерывна слева, так как она постоянна на полуинтервалах (xi; xi+1].

Функция F(x) распределения генеральной совокупности, в отличие от эмпирической функции F*(x) распределения выборки, называют теоретической функцией распределения. Различие между эмпирической и теоретической функциями распределения состоит в том, что первая определяет относительную частоту события X < x, вторая – вероятность того же события. Эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности.

Пример 5. Построить эмпирическую функцию по распределению выборки (табл. 6).

Решение. Объём выборки n = 2 + 3 + 10 + 5 = 20. Тогда по определению искомая эмпирическая функция определяется формулами:

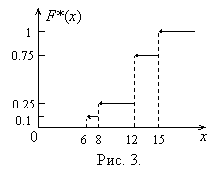F*(x) =

График этой функции изображён на рис. 3.

Пример 6 (Самый застенчивый холостяк) (для самостоятельного решения). В «Службу знакомств» города Энска тестировались 50 представителей мужского пола в возрасте от 18 до 50 лет с целью определения уровня тревожности при обращении их в данную службу. Получилось статистическое распределение уровня тревожности, указанное в табл. 7.

Предлагается построить эмпирическую функцию распределения и найти, как часто указанный показатель будет попадать в границы от 7 до 20. Указать признак самого застенчивого мужчины, посетившего «Службу знакомств» города Энска. Как часто там бывали такие мужчины?

Числовые характеристики вариационных рядов

Пусть все объекты наблюдения изучают относительно некоторого количественного признака Х. Они образуют генеральную совокупность объемом N. Статистическая таблица частот генеральной совокупности имеет вид

где

Определение 1. Генеральной средней называется постоянная, равная сумме произведений значений вариантов на соответствующие значения относительных частот

.

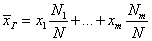Определение 2. Генеральной дисперсией называется число, равное .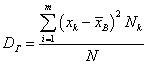

Определение 3. Генеральным средним квадратическим отклонением называется .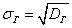

На практике обычно из генеральной совокупности случайным образом выбирают n объектов и изучают полученную выборку, подсчитывая выборочную среднюю и выборочную дисперсию.

Определение 4. Выборочной средней называется постоянная, равная сумме произведений значений вариантов на соответствующие значения относительных частот

.

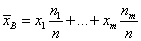Пример 1. Имеются данные о заработной плате

Вычислим выборочное среднее

- средняя заработная плата.

Определение 5. Размахом вариации R называется разность между наибольшим и наименьшим значениями вариант . Модой М0 называется значение варианты, встречающееся с наибольшей частотой, т. е. наиболее типичное в данном вариационном ряду. Медианой Ме называется значение варианты, лежащее в середине вариационного ряда, если этот ряд имеет нечетное число членов, и среднее арифметическое двух значений вариант, расположенных в середине ряда, если ряд состоит из четного числа членов.

В предыдущем примере,

R = 2000 – 1000 = 1000,

М0 = 1700,

Ме = 1500, т. е. половина сотрудников получает заработную плату, выше 1500.

Определение 6. Выборочной дисперсией называется число, равное .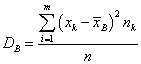

Пример 2 (для самостоятельного решения). Найти оценку разброса скорости чтения, распределение которой представлено в табл. 10. Предварительно определите, какова относительная частота средней скорости чтения.

Выборочная средняя, найденная по данным одной выборки, является определенным числом. Если же извлечь из генеральной совокупности другие выборки, то выборочная средняя будет меняться, следовательно, является случайной величиной .

Теорема 1. Математическое ожидание случайной величины равно генеральной средней

. 

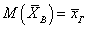Пусть требуется по данным выборки оценить неизвестную генеральную совокупность. Если найти выборочную дисперсию и принять ее в качестве оценки генеральной дисперсии, то получим заниженное значение.

Теорема 2. Математическое ожидание выборочной дисперсии связано с генеральной дисперсией формулой . 

Статистическое оценивание

Допустим, требуется определить количественный признак генеральной совокупности. В распоряжении исследователя имеются лишь данные выборки (x1, x2, …, xn), полученные в результате n наблюдений. Тогда исследуемый параметр выражают через эти данные с помощью однозначно определённой функции, называемой оценкой или статистикой параметра.

Существует два рода оценок: точечные, когда неизвестный параметр Θ характеризуется приближённым значением Θ*, и интервальные, когда неизвестный параметр характеризуется интервалом возможных значений.

Пусть количественный признак Х (случайная величина) подчиняется закону распределения F(Х, Θ), причем вид F(Х, Θ) известен, а параметр требуется определить.

Исследовать все элементы генеральной совокупности для определения Θ невозможно, поэтому об этом параметре судят по выборкам из генеральной совокупности.

Определение 1. Точечной оценкой параметра Θ называют функцию результатов наблюдений Θ*(x1, x2, …, xn). Эта оценка зависит от объёма выборки n и её представителей x1, x2, …, xn. Поэтому она является случайной величиной, т. е. Θ* – случайная величина.

Если при определении Θ* возможны систематические ошибки, то эта оценка будет давать приближённое значение Θ с избытком (или с недостатком). В этом случае и математическое ожидание случайной величины Θ* будет больше, чем Θ (или меньше), т. е. полученная оценка будет смещённой. Только соблюдение требования М(Θ*) = Θ гарантирует от систематических ошибок.

Определение 2. Оценка параметра называется несмещённой, если математическое ожидание Θ* равно Θ, т. е. М(Θ*) = Θ.

Определение 3. Состоятельной называют статистическую оценку, которая при n→∞ стремится по вероятности к оцениваемому параметру, т. е. при любом ε > 0 вероятность того, что оценка отличается от параметра не больше, чем на ε, сколь угодно близка к единице.

Кроме того, мы должны потребовать, чтобы разброс возможных значений Θ* вокруг средней величины (математического ожидания) был как можно меньше, т. е. чтобы дисперсия (мера разброса) была минимальной.

Определение 4. Оценка называется эффективной, если имеет наименьшую возможную дисперсию, т. е. D(Θ*) = Dmin.

Выборочную среднюю принимают в качестве точечной оценки генеральной средней. И эта оценка является несмещённой и состоятельной.

Несмещенной оценкой генеральной средней (математического ожидания) является выборочная средняя .

Смещенная оценка генеральной дисперсии является выборочная дисперсия .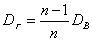

Несмещенная оценка генеральной дисперсии является исправленная дисперсия .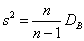

Метод моментов заключается в вычислении из известных тождеств, в которых несколько важнейших числовых характеристик (моментов) теоретического распределения заменяются их оценками. Например, для равномерного распределения известно, что

М(X) = , D(X) =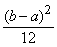, где a и b – параметры.

Согласно методу моментов полагаем,

М(X) = mx*, D(X) = Dx*, где mx* и Dx* – оценки.

Отсюда получаем оценки параметров:

a* = mx* – sx* и b* = mx* + sx*.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5