1) Sie bleiben in diesem Dorf für einige Tage. (beabsichtigen)
2) Die Freunde machen eine interessante Fahrt mit ihrem eigenen Wagen.(sich verabreden)
3) Sie fährt in diesem Sommer in die Türkei.(empfehlen)
4) Irena und ihre Kollegen verbringen das Wochenende an der See. (die Absicht haben).
Преобразуйте инфинитивные группы в дополнительные придаточные предложения.1) Ich hoffe während des Urlaubs viele Städte zu besichtigen.
2) Wir freuen uns einen Ausflug nach K. Unternehmen zu können.
3) Vergiss nicht während der Fahrt zweimal umzusteigen!
Составьте придаточное условное предложение.1) Sie können zum Bahnhof auch zu Fuss gehen, wenn (viel Zeit haben).
2) Sie müssen hier länger bleiben, wenn (die bedeutendsten Theater der Hauptstadt besuchen wollen)
3) Man muss den Urlaub im voraus plannen, wenn (gut verbringen).
Переведите на немецкий язык
1) К сожалению, я был очень занят и не смог осмотреть все достопримечательности этого старого города.
2) Я смог побывать в Третьяковской галерее и многих музеях.
3) Я узнал много нового и интересного об этом городе.
4) Москва – один из крупнейших современных городов.
Переведите тексты
Nordfriesland. Insel Sylt.
Mehr als eine Insel! 40 km feiner Sandstrand. Raue Brandung an der Westseite; stilles Wattenmeer im Osten. Dünen und grüne Deiche. Blühende Heide und majestätische kliffs. Tagträume und Nachtleben. Truben und Abgeschiedenheit. Orte – keiner wie der andere und jeder mit unverwechselbaren Charme...
Urlaub auf Sylt – endlich Zeit für sich selbst. Zeit für einen gemütlichen Einkaufsbummel, allein, zu zweit oder mit der ganzen Familie.
Sonne und Schwimmen, Spielen und Strandgymnastik, an Sylts Stränden können Sie viel erleben.
Willkommen auf Deutschlands Partyinsel Nummer 1!
Westerland – Hery und Mittelpunkt der Insel! Hier pulsiert das Leben. Sie finden alles, was gute Ferien ausmacht. Weite Sandstrände, die Flaniermeile „Friedrichstrasse“, Idyle in Altwesterland und die zentrale Lage. Optimaler Ausgangspunkt für Ausflüge.
Flughafen – Westerland.
Bahnstation – Westerland.
Fährhafen. Hotels. Ferienwohnungen.
Touren und Ausflüge
„Eine Welt – zwei Ozeane“ zeigt das Syltaquarium in faszinierenden Unterwasserwelten. 30 Becken mit Unterwassertunnel laden zur Reise durch die Weltmeere ein. Täglich legen die Schiffe zu zahlreichen Ausflügen ab: mit dem Erlebniskutter zum Fischfang. Fahrten yu den Seehundbänken, nach Föhr, Helgoland, durch das Wattenmeer.
Erleben Sie die Schönheit der Insel aus der Vogelperspektive – ein Rundflug über Sylt ist ein unvergessliches Erlebnis.
St. Peter-Ording bietet Ihnen ein buntes Programm: osterfeuer, Konzerte – zum Beispiel im Rahmen des Schleswig-Holstein Musikfestivals. Das Beach-Volleyball, Masters-Turnier, Chor-Abend, das Nivea-Strandfest oder die Strandsegelmeisterschaften.
Das neue Attraktion ab Frühjahr 2006 – die Sturmflut-Erlebniswelt „Blanker Hans“. Eine für Schleswig-Holstein einzigartige Erlebniswelt, die ihnen ein weiteres Highlight bietet. Hier erleben Sie die enormen Naturgewalten sinnlich und spielerisch in 3D.
3.8. Математика
Контрольная работа № 3, 4
Задания для контрольных работ № 3, 4 по математике изданы отдельным методическим пособием.
3.9. Информатика
Контрольные задания по информатике изданы отдельным методическим пособием.
3.10. Инженерная графика
Для выполнения контрольной работы по дисциплине «Инженерная графика» студентам заочного отделения предлагается расскрыть один из предложенных вопросов.
Вариант № 1. (Выполняется студентами с нечетным номером зачетной книжки)
Виды изделий и конструкторских документов. Содержание графической и текстовой документации.
Вариант №2. (Выполняется студентами с четным номером зачетной книжки)
Основные положения АКД (программы Auto Card).
Рекомендованная литература
Локтев курс начертательной геометрии. – М.: высшая школа, 1999. Основы AutoCad для версий 14 и 2000. Ч.1. Создание конструкторской документации: Учеб.-метод. пособие / Сост.: , , . – СПб.: СПбГИЭУ, 2000. Основы AutoCad для версий 14 и 2000. Ч.2. Работа в трехмерном пространстве: Учеб.-метод. пособие / Сост.: , , . – СПб.: СПбГИЭУ, 2000. Сборник заданий по инженерной графике с примерами выполнения чертежей на компьютере: Учебное пособие / , , – 3-е изд., испр. и доп. – М.: Высш. шк., 2003. – 355 с. Чекмарев графика. – М.: Высшая школа, 2000.3.11. Теоретические основы прогрессивных технологий
Контрольная работа № 2.
1. Роль математики в современном естествознании.
2. Главные выводы специальной и общей теории относительности.
3. Проблемы соотношения вещества и поля, материи и энергии.
4. Современные представления о пространстве и времени.
5. Характеристика основных физических взаимодействий.
6. Основные проблемы современной химии.
7. Проблема сущности живого и его отличия от неживой материи.
8. Основные проблемы генетики и роль воспроизводства в развитии живого.
9. Роль симметрии и ассиметрии в научном познании.
10. Механизмы обратной связи и их значение.
Литература
1. , Марголис каталитическое окисление органических веществ. – М.: Химия, 1985. – 192с.
2. Кибернетика. М., 1968.
3. Краткий справочник физико-химических величин. Изд. 8-е, перераб. / Под. ред. , . – Л.: Химия, 1983. – 232с.
4. Масленникова и мембранная технология: Учеб. пособие по разд. дисц. "Концепция современного естествознания" для инженерно - экон. спец./ СПбГИЭА. – СПб., 1994. – 71с.
5. Научные основы прогрессивной техники и технологии / , , и др. – М.: Машиностроение, 1986. – 376с.
6. Очистка сточных вод в биофильтрах и аэротенках: Метод. указ. /Сост. / ЛТИ. – Л., 1989. – 30с.
7. Время, хаос, квант. М., 1994.
8. Две культуры. М., 1983.
9. Сысоева основы физико-химических измерений в электрохимической технологии: Учеб. пособие / ЛТИ. – Л., 1985. – 91с.
10. , Ческих . Контроль химической, бактериальной и радиационной безопасности по международным стандартам. Справочник / Под. ред. . – М.: Изд-во "Геликон", 1992. – 392.
11. Химический энциклопедический словарь / Советская энциклопедия, 1983. – 792с.
12. Эволюция физики. М., 1965.
13. Ядерная и термоядерная энергетика будущего / Под. ред. . – М.: Энергоатомиздат, 198с.
3.12. Экология
Контрольная работа
Контрольная работа по экологии состоит из двух вопросов, выбираемых в соответствии с последним номером зачетной книжки.
Вопрос №1: ««Характеристика одной их экосистем основных ландшафтных зон Земного шара (по выбору)»
Предлагаемые экосистемы:
1. Экосистемы арктических пустынь и тундр.
2. Экосистемы тайги.
3. Экосистемы смешанных и широколиственных лесов умеренного пояса.
4. Экосистемы жестколистных вечнозеленых лесов Средиземноморья.
5. Экосистемы муссонных лесов.
6. Экосистемы степей и прерий.
7. Экосистемы пустынь.
8. Экосистемы влажных тропических лесов.
9. Экосистемы океанов и морей.
10. Экосистемы горных территорий.
План характеристики
1. Географическое положение.
2. Примеры природных объектов, представляющих систему.
3. Рельеф местности как фактор развития экосистемы.
4. Климатические условия: продолжительность вегетационного периода, средняя температура июля и января, количество осадков и их распределение по сезонам, основные типы воздушных масс и преобладающие ветра.
5. Водный фактор.
6. Коры выветривания и типы почв.
7. Основные типы ландшафтов.
8. Животные и растительные сообщества: видовое разнообразие.
9. Классификационные типы представителей флоры и фауны, их экологические характеристики.
10. Продуктивность и биомасса биоценоза.
11. Факторы, определяющие устойчивость экосистемы.
12. Виды и характер антропогенного использования экосистемы (существующие и возможные).
13. Антропогенное воздействие и его последствия.
14. Элементы эстетической привлекательности экосистемы.
15. Наличие и виды особо охраняемых территорий.
Вопрос №2: «Пути сохранения биоразнообразия и генофонда биосферы»
Специальность 080502 «Экономика и управление на предприятии траспорта»
1 вариант
Государственные природные заповедники, природные заказники и памятники природы
2 вариант
Национальные природные парки и музеи-заповедники. Курортные и лечебные оздоровительные зоны
Специальность 080502 «Экономика и управление на предприятии городского хозяйства»
1 вариант
Экологическая катастрофа, причины и последствия
2 вариант
Экологический кризис и его основные показатели
Список рекомендованной литературы
1. , Торшин человека. М.. 1994.
2. , Бондарев и цивилизация. М.. 1988.
3. Бобылев экономического развития. М.. 1994.
4. Растительность Земного шара. Т 1-3. М., 1969-75.
5. Вернадский . Разл. Изд.
6. , Ширкова и культура. М.. 1989.
7. Горелов . М., 1998.
8. Камшилов биосферы. М., 1981.
9. Максаковский картина мира. Т. 1-2, М., .
10. Малхазова -географический анализ территорий. М.. 2001.
11. , Суравегина . М.. 1996.
12. Основы экологии. М., 1975.
13. Реймерс . М., 1994.
14. , Пустовойтов экология. М., 2000.
15. Экология. Ростов-н-Д., 2000.
3.13. Материаловедение
Контрольная работа выполняется студентами-заочниками специальности 080502.65 «Экономика и управление на предприятиях городского хозяйства» в соответствии с рабочей программой дисциплины «Материаловедение».
Целью выполнения контрольной работы является углубленное самостоятельное изучение студентами наиболее значимых разделов дисциплины «Материаловедение». Полученные студентами навыки при выполнении контрольной работы позволят им более сознательно изучить по рекомендуемой литературе весь учебный теоретический материал и самостоятельно подготовиться к сдаче зачета по дисциплине.
В контрольной работе студенты должны изложить правильные и аргументированные ответы на предлагаемые вопросы, решить по одной задаче из предложенных по каждой теме. Реферативное описание ответов на поставленные вопросы должно обязательно иллюстрироваться рисунками, схемами и конкретными примерами.
Контрольная работа разработана по 10 вариантам индивидуальных заданий, которые включают в себя вопросы, охватывающие наиболее важный объем теоретического материала по изучению дисциплины, задачу по расчету состава бетонов и задачи по темам курса.
Вариант I
1.Перечислите основные способы антикоррозионной защиты металлических, бетонных, железобетонных, деревянных конструкций.
2.Виды извести: состав, свойства, особенности получения, области применения.
3.Задачи (см. таблицу).
Вариант II
1.Приведите 5-6 примеров, иллюстрирующих взаимосвязь строения, состава и свойств материалов.
2.Виды и сущность холодной и горячей обработки металлов. Структура стали в неравновесном состоянии и виды ее термической обработки.
3.Задачи (см. таблицу).
Вариант III
1.Классификация природных каменных материалов по условиям образования. Приведите по 2-3 примера для каждой группы, сравните их по минералогическому составу, основным свойствам. Опишите области их применения в строительстве и городском хозяйстве.
2.Особенности строительных растворов, отличающие их от бетонов.
3.Задачи (см. таблицу).
Вариант IV
1.Приведите примеры композиционных материалов, опишите их состав и строение.
2.Виды керамических материалов и изделий, применяемых в строительстве. Общая схема технологии их производства.
3.Задачи (см. таблицу).
Вариант V
1.Пороки древесины (проиллюстрируйте ваш ответ рисунками).
2. Разновидности портландцемента и их сопоставление по составу, свойствам и областям применения с портландцементом.
3.Задачи (см. таблицу).
Вариант VI
1.Виды гипсовых вяжущих, их свойства, особенности получения. Твердение гипсовых вяжущих. Строительные материалы и изделия на основе гипса.
2.Основные компоненты лакокрасочных составов: пигменты, олифы, наполнители – их свойства и назначение.
3.Задачи (см. таблицу).
Вариант VII
1.Свойства битумов и дегтей, основные области их применения. Изложите порядок расчета состава бетонной смеси. Каковы основные принципы и критерии при определении марки бетона.
2.Состав и назначение основных компонентов пластмасс. Материалы и изделия из пластмасс: свойства образующих полимеров и области применения пластмасс.
3.Задачи (см. таблицу).
Задача «Расчет состава бетонов» (3)
А) По имеющимся исходным данным, приведенным в таблице 1, рассчитать недостающие показатели, характеризующие бетоны.
Таблица 1
Характеристики бетона |
Номер варианта | ||||
|
1; 9 |
2; 6 |
3; 8 |
4; 7 |
5; 10 | |
|
Марка цемента (Rц) |
300 |
300 |
? |
500 |
300 |
|
Марка бетона (Rб ) |
100 |
? |
? |
? |
400 |
|
Цементно-водное отношение (Ц/В) |
? |
3 |
1,5 |
? |
? |
|
Качество заполнителей (А) |
0,6 |
- |
0,55 |
? |
- |
|
Качество заполнителей (А1) |
- |
0,4 |
- |
- |
0,43 |
|
Прочность бетона в возрасте 28 сут., МПа |
10 |
? |
? |
? |
? |
|
Прочность бетона в возрасте 90 сут., МПа |
? |
? |
30 |
20 |
? |
|
Расход воды (В), л/м3 |
190 |
190 |
190 |
180 |
? |
|
Расход цемента (Ц), кг/м3 |
? |
? |
? |
180 |
480 |
Методика решения (3).
Недостающие данные, которые требуется найти, определяются с использованием формулы проф. :
для бетонов с Ц/В![]() 2,5
2,5
![]()
![]()
R б = Rц А ![]() – 0 ,5 (1)
– 0 ,5 (1)
для бетонов с Ц/В > 2,5
![]()
![]()
Rб = Rц А1 ![]() + 0,5 (2)
+ 0,5 (2)
где Rц – активность цемента;
Rб – марка бетона, определяемая по прочности бетона в возрасте 28 суток нормального твердения;
A, А1 – коэффициенты, характеризующие качество используемых заполнителей и цемента.
Для бетонов характерно увеличение прочности с течением времени, нарастание прочности происходит по логарифмическому закону:
Rn = R28 ![]() (3)
(3)
где R n – прочность бетона в возрасте n суток, R28 – марка бетона, n – число дней твердения.
Б) На основе исходных данных и рассчитанных значений в табл. 1 определить состав компонентов бетонной смеси.
Общими для всех вариантов являются следующие данные.
Истинные плотности: цемента рц=3100 кг/м3;
песка рп=2200 кг/м3;
крупного заполнителя (щебня) рщ=2600 кг/м3;
насыпная плотность щебня рнщ=1400 кг/м3.
Методика решения (3).
После определения цементно-водного отношения и расхода цемента определим расходы мелкого и крупного заполнителя исходя из следующих положений.
Объем 1м3 (1000 дм3) плотно уложенного бетона слагается из объема зерен мелкого и крупного заполнителей и цементного теста, заполняющего пустоты между зернами заполнителей, что выражается уравнением абсолютных объемов (4):
![]() +
+ ![]() +
+ ![]() +
+ ![]() = 1 (4)
= 1 (4)
где Ц, В, П, Щ - расходы соответственно цемента, воды, песка и крупного заполнителя (щебня), кг;
![]() ,
, ![]() ,
, ![]() - истинные плотности этих материалов, кг /м3 .
- истинные плотности этих материалов, кг /м3 .
Пустоты между зерен должны быть заполнены раствором. При равенстве растворной смеси объему межзерновых пустот такую бетонную смесь уложить нельзя, так как зерна не будут склеиваться между собой из-за отсутствия свободного цементного слоя на поверхности зерен. Каждое зерно должно обволакиваться цементом или растворной смесью, однако при этом зерна раздвигаются, то есть увеличивается объем межзерновых пустот. Увеличение объема межзерновых пустот учитывается коэффициентом раздвижки зерен (Kpaзд). Данное положение иллюстрируется выражением (5).
![]() =
= ![]() +
+ ![]() +
+ ![]() (5)
(5)
где ![]() - насыпная плотность щебня;
- насыпная плотность щебня;
Vпуст – пустотность крупного заполнителя, определяемая по формуле (6):
V = (6)
Коэффициент раздвижки для пластичных смесей определяется по таблице в зависимости от объема цементного теста (по формуле 7 и таблице 2):
Vцт =![]() +
+ ![]() (7)
(7)
Таблица 2
Значения К разд для пластичных бетонных смесей
|
Vцт.дм3 |
200 |
225 |
250 |
275 |
300 |
325 |
350 |
375 |
400 |
|
Кразд |
1,2 |
1,25 |
1,32 |
1,36 |
1,42 |
1,45 |
1,48 |
1,53 |
1,55 |
Решая совместно уравнения (4) и (5) получаем формулу для определения расхода крупного заполнителя:
Щ = 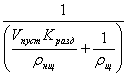 (8)
(8)
Расход мелкого заполнителя (песка) определяем из формулы (9)
П = 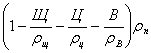 (9)
(9)
Найденный состав бетона в виде расхода основных компонентов выражают в виде соотношения (10) основных компонентов к массе цемента.
1 : В/Ц : П/Ц : Щ/Ц (10)
Рекомендованная литература
Основная
Байер материалы: Учебник. – М.: Архитектура-С, 2004. – 240 с., ил. * , Федюкин : Учеб. пособие по спец. 060816 /СПбГИЭУ. – СПб., 1997. – 82 с. * Материаловедение. Методические указания к контрольным работам для студентов заочной формы обучения института региональной экономики и управления./Составитель . – СПб.: СПбГИЭУ, 2002, 10 с. * Строительные материалы: Учебник /Под общей ред. – М.: Изд-во АСВ, 2000. – 536 с., с илл. *Дополнительная
, Ткаченко строителя. 5-е изд., доп. и перераб. – Ростов н/Д.: Феникс, 2004. – 480 с.* Баженов бетона. - М., 1987. Батраков бетоны. - М., 1999. и др. Сухие смеси в современном строительстве /Под. ред. . Новосибирск, 1998. , Гончаров изделий из древесины. - М.: Стройиздат, 1985. Волженский вяжущие вещества. - М.,1986. , Котова для арматурщика-бетонщика. - М., 1994. Горлов теплоизоляционных материалов и изделий. - М.: Высшая школа, 1989. Домокеев материалы. - М.: Высшая школа, 1989. , В, Строительные материалы и изделия. - Мн: «Дизайн - ПРО», 2001. Комар материалы. - М., 1988. Материаловедение и технология металлов: Учеб. для студентов машиностроит. спец. вузов /, , и др.; под ред. . – М.: Высш. шк., 2002. – 638 с.: ил. * Материалы для конструирования защитных покрытий. Учеб. пособие/ ., , ; под редакцией : Изд-во АСВ, 2000. – 180 с. * Онищенко работы в строительстве. - М.: Высшая школа, 1989. Оценка качества строительных материалов: Учебное пособие /, , – М.: изд-во АСВ, 1999. – 240 с., ил. * , Рояк цементы. - М., 1989. , Федюкин технологии заготовительного производства: Учеб. пособие. – СПб.: СПбГИЭУ, 2003. – 116 с. * , Кухаренко материалы и изделия. Сборник задач. - М.,199с.* - звездочкой помечены книги, имеющиеся в библиотеке филиала СПбГИЭУ г. Твери
3.14. Статистика
Общие указания
Контрольные работы по дисциплине "Статистика" выполняются студентами заочной формы обучения для закрепления теоретических знаний и отработки практических навыков применения статистических методов и приемов при обработке статистической информации.
Студенты заочной формы обучения выполняют две контрольные работы. При выполнении контрольных работ необходимо обратить особое внимание на следующие требования:
1. Задания к контрольной работе составлены в 100 вариантах. Каждый студент выполняет один вариант. Номер его варианта соответствует последним двум цифрам номера его зачетной книжки (см. Приложение, табл. 1). Замена задач не допускается. Номер варианта указывается в самом начале каждой контрольной работы.
2. Нельзя ограничиваться приведением только готовых ответов. Расчеты должны быть представлены в развернутом виде, применяя, где это необходимо, табличное оформление исходной информации и расчетов, со всеми формулами, пояснениями и выводами, соблюдая достаточную точность вычислений. В пояснениях и выводах необходимо показать, что именно и как характеризует исчисленный показатель.
3. Работа должна быть написана разборчиво, без помарок. На обложке необходимо указать фамилию, имя, отчество, курс, номер зачетной книжки. Работа должна быть подписана студентом с указанием даты выполнения работы.
4. Контрольная работа должна быть представлена в установленные сроки.
5. Если работа не принимается к зачету, то она возвращается студенту. Студент обязан учесть все замечания и внести их в текст работы или выполнить ее заново. Несамостоятельно выполненные работы рассматриваются как неудовлетворительные и не зачитываются.
6. За консультацией по всем вопросам, возникшим в процессе изучения курса статистики и выполнения контрольных работ, следует обращаться к преподавателю
Для выполнения контрольной работы рекомендуется литература:
1. Теория статистики: Учебник / Под. ред. проф. . – изд 3-е, перераб. и доп. – М.: Финансы и статистика, 20с.
2. , Юзбашев теория статистики: Учебник; Под ред. чл.-корр. РАН . – изд. 4-е, перераб. и доп. - М.: Финансы и статистика, 20с.
3. Гусаров : Учебное пособие. - М.: ЮНИТИ-ДАНА, 20с.
4. , , и др. Статистика: Учебное пособие; Под ред. . – изд. 2-е, перераб. и доп. – М.: ИНФРА – М, 20с.
КОНТРОЛЬНАЯ РАБОТА №l
Теория статистики исследует количественные соотношения в массовых явлениях любой природы, в том числе в экономике. Метод статистики заключается в получении статистической характеристики для совокупности в целом путем обобщения данных об ее отдельных элементах. На большой массе явлений, через преодоление случайности, проявляется статистическая закономерность, поэтому все статистические показатели характеризуют некоторую закономерность.
Статистические характеристики (показатели) могут быть получены на основе статистического исследования, которое состоит из трех основных этапов:
1.Статистическое наблюдение, которое представляет собой сбор
первичных данных об отдельных элементах совокупности.
2. Первичная обработка результатов наблюдения, их контроль, группировка и сводка материалов наблюдения.
3. Анализ материалов наблюдения, определение численных статистических характеристик, анализ статистических зависимостей.
Для каждого этапа характерен определенный набор статистических приемов, умение использовать которые должны показать студенты при выполнении заданий контрольной работы.
Задание №1
На основе данных, приведенных в Приложении и соответствующих Вашему варианту (таблицы 1 и 6), выполнить:
1. Структурную равноинтервальную группировку по обоим признакам. Если вариация группировочного признака значительна и его значение для отдельных групп необходимо представить в виде интервалов, то при построении группировки по признаку № 1 принять число групп равным 7, а по признаку №Результаты представить в таблице, сделать выводы.
2. Аналитическую группировку, для этого определить признак-результат и признак-фактор, обосновав их выбор. При построении аналитической группировки использовать равнонаполненную группировку по признаку-фактору (в каждой группе приблизительно одинаковое количество наблюдений). Результаты группировки представить в таблице. Сделать выводы о наличии и направлении взаимосвязи между признаками.
3. Комбинационную группировку по признаку-фактору и признаку-результату. Сделать выводы.
Группировка статистических данных.
Группировка - это распределение единиц совокупности по группам в соответствии с группировочным признаком. Назначение группировки состоит в том, что этот метод обеспечивает обобщение данных, представление их в компактном, обозримом виде. На основе группировки рассчитываются сводные показатели по группам, появляется возможность их сравнения, изучения взаимосвязей между признаками.
Различия в целевом назначении группировки выражаются в существующей в нашей статистике классификации группировок: типологические, структурные, аналитические.
При осуществлении любой группировки решается вопрос об определении числа выделяемых групп. При группировке по количественному признаку вопрос о числе групп решается на основе выделения однородных, близких по значению признака единиц совокупности. Необходимо, чтобы каждая группа характеризовала существенные типы явления. Число единиц в выделенных группах должно быть достаточным, чтобы характеристики, рассчитанные для отдельных групп, были статистически устойчивыми. Количество выделяемых групп зависит от вариации признака, числа наблюдений, а также от количества отдельных возможных значений признака, т. е. от числа вариант признака. При небольшом числе вариант признака, положенного в основу группировки, каждая варианта представляет отдельную группу.
Если число вариант велико, то значения группировочного признака для отдельных групп указываются в интервалах "от - до". Для этого всю область изменения признака разбивают на несколько интервалов и считают, сколько элементов попадает в отдельный интервал. Интервалы могут быть равными и неравными, открытыми и закрытыми. Группировку с неравными интервалами надо использовать, если размах вариации признака в совокупности велик, неравные интервалы применяются как прогрессивно возрастающие или убывающие. В этом случае границы каждого интервала устанавливаются исследователем. Однако необходимо учесть, что наличие равных интервалов технически значительно облегчает вычисление различных статистических характеристик.
Равные интервалы применяются в случаях, когда изменение признака внутри совокупности происходит равномерно. Расчет величины интервала при равных интервалах производится по формуле:
D=(x max –xmin) / K,
где D - величина отдельного интервала,
x max - максимальное значение признака в исследуемой совокупности;
xmin - минимальное значение признака в исследуемой совокупности;
К - число групп.
Затем определяются границы каждого интервала:
для первого интервала: от xmin до xmin +D;
для второго интервала: от xmin +D до xmin +2D;
…………………………………………………..
для интервала: n от xmin +КD до x max.
Типологическая группировка служит для выявления типов элементов явлений. Структурная группировка служит для исследования совокупности по одному признаку.
После того, как в результате сводки статистические данные сгруппированы, они, как правило, представляются в виде таблицы. Макет таблицы для представления результатов структурной группировки может выглядеть следующим образом:
Наименование таблицы
|
Наименование группировочного признака, (единицы измерения) |
Количество единиц совокупности в отдельной группе |
В процентах к итогу |
|
1 |
2 |
3 |
|
… |
… |
… |
|
… |
… |
… |
|
… |
… |
… |
|
Итого |
Общее число элементов совокупности |
100 |
Здесь в первой графе указываются варианты (интервалы) значений признака-фактора для отдельных групп по возрастанию или убыванию.
Аналитические группировки служат для выявления аналитической зависимости между группировочными признаками. При построении аналитических группировок важно правильно определить признак-результат и признак-фактор. Признак, влияние которого на другие признаки исследуется, называется признаком-фактором. Признак, испытывающий влияние факторного, называется признаком - результатом. Чтобы установить связь между признаками, аналитическая группировка осуществляется по признаку-фактору. Затем по каждой группе отбираются соответствующие значения признака-результата и рассчитывается его среднее значение. Сопоставляя изменение средних значений признака-результата от группы к группе с изменениями признака-фактора можно сделать вывод о наличии или отсутствии взаимосвязи, а также о ее направлении. Различие групповых средних позволяет утверждать, что признаки взаимозависимы. Если изменение величины признака-фактора в определенном направлении вызывает изменение величины признака-результата в том же направлении, то связь прямая, в противном случае - связь обратная.
Макет таблицы для представления результатов аналитической группировки может выглядеть следующим образом:
Наименование таблицы
|
Наименование признака-фактора, (единица измерения) |
Количество единиц совокупности в отдельной группе |
Среднее значение признака-результата (единица измерения) |
|
… |
… |
… |
|
… |
… |
… |
|
… |
… |
… |
|
Итого |
Общее число элементов совокупности |
- |
Здесь в первой графе указываются варианты (интервалы) значений признака-фактора для отдельных групп по возрастанию или убыванию.
Проследить зависимость между факторами можно также на основе комбинационной группировки. Комбинационная группировка осуществляется одновременно по двум и более признакам, взятым в сочетании.
Макет комбинационной таблицы выглядит следующим образом:
Наименование таблицы
|
Группировка по признаку-фактору |
Группировка по признаку-результату |
Всего | |||
|
n11 |
n12 |
… |
n1M |
Σ nij | |
|
n21 |
N22 |
… |
n2M |
Σ n2j | |
|
… |
… |
… |
… |
… | |
|
nK1 |
nk2 |
… |
NKM |
Σ nMj | |
|
Всего |
Σ ni1 |
Σ ni2 |
… |
Σ niK |
Σ nij |
Здесь nij - частота совместного появления значения i признака-фактора (i = 1,2,… , М) и значения j признака результата (j= 1,2, …, K).
Если наибольшие частоты каждой строки и каждого столбца располагаются вдоль диагонали таблицы, идущей от левого верхнего угла таблицы к правому нижнему, то можно сделать вывод, что связь между признаками является прямой и близкой к линейной.
Если наибольшие частоты располагаются вдоль диагонали от правого верхнего угла к нижнему левому, то связь — обратная и близкая к линейной.
Если частоты во всех клетках таблицы примерно одинаковы, то связи между признаками нет.
Задание №2
1. На основе равноинтервальной структурной группировки (для любого признака) построить вариационный частотный и кумулятивный ряды распределения, оформить в таблице, изобразить графически.
2. Проанализировать вариационный ряд распределения, вычислив:
· среднее арифметическое значение признака;
· медиану и моду, квартили и децили распределения;
· среднее квадратичное отклонение;
· коэффициент вариации.
3. Проверить теорему о разложении дисперсии, используя данные
аналитической группировки.
4. Сделать выводы.
Обобщающие характеристики совокупностей
Анализ статистических совокупностей включает в себя: построение рядов распределения; графическое представление распределения; определение характеристик центра распределения, показателей вариации.
Рядами распределения называют числовые ряды, характеризующие структуру совокупности по некоторому признаку. Ряд распределения может быть получен в результате структурной группировки. Ряд распределения, образованный по количественному признаку (он называется вариационным радом), может быть дискретным, если значения признака выражены целыми числами и каждая варианта представлена в вариационном ряде отдельной группой, или интервальным (непрерывным), если значения признака выражены вещественными числами или число вариант признака достаточно велико.
Ряд распределения состоит из следующих элементов:
xi - варианта- отдельное, возможное значение признака i=1,2,...,К, где К - число значений признака;
Ni - частоты - численность отдельных групп соответствующих значений признаков;
N - объём совокупности - общее число элементов совокупности;
qi - частость - доля отдельных групп во всей совокупности;
Di - величина интервала.
Если вариационный ряд представлен неравными интервалами, то рассчитывается абсолютная и относительная плотности распределения.
Абсолютная плотность h - это отношение частоты к величине интервала, а относительная плотность ![]() - это отношение частости к величине интервала:
- это отношение частости к величине интервала:
hi=Ni /Di, ![]() = qi /Di.
= qi /Di.
Полученный вариационный ряд оформляется в виде таблицы, где в первой графе указываются варианты (интервалы) значений признака, а в следующих графах - частота, частость или, если необходимо, абсолютная или относительная плотность распределения.
Ряд распределения по частоте (частости) в целом характеризует структуру совокупности по данному признаку. Однако для описания распределения совокупность могут использоваться и кумулятивные ряды, т. е. ряды накопленных частот (или частостей), которые иногда имеют даже некоторые преимущества.
Накопленная частота (частость) данного значения признака - это число (доля) элементов совокупности, индивидуальные значения признака которых не превышают данного.
Обозначим: F(x) - накопленная частота для данного значения х; G(x) - накопленная частость для данного значения х.
Эти характеристики обладают следующими свойствами:
![]()
Рассмотрим интервалы 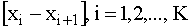 :
:
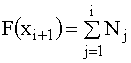 .
.
Первым этапом изучения вариационного ряда является его графическое изображение. Способы построения графиков для разных видов рядов распределения различны.
Изображением дискретного ряда распределения является полигон. В системе координат по оси абсцисс откладываются варианты ![]() , по оси ординат - частоты (частости), затем отмечают точки с координатами (
, по оси ординат - частоты (частости), затем отмечают точки с координатами (![]() ), которые последовательно соединяются отрезками прямой.
), которые последовательно соединяются отрезками прямой.
Интервальный ряд распределения изображается графически в виде гистограммы. При ее построении на оси абсцисс откладывают интервалы ряда. Над осью абсцисс строятся прямоугольники, основанием которых является интервал, а высота - соответствующая этому интервалу плотность распределения (или частота, частость - если ряд равноинтервальный).
Изображением ряда накопленных частот служит кумулята. Накопленные частоты наносятся в системе координат в виде ординат для границ интервалов; соединяя нанесенные точки отрезками прямых, получаем кумуляту.
Вторым этапом изучения вариационного ряда является определение характеристик центра распределения. Характеристика центра распределения представляет собой такую величину, которая в некотором отношении характерна для данного распределения и является его центральной величиной.
К характеристикам центра распределения относятся: средняя арифметическая, медиана, мода.
Для сгруппированных данных, представленных в вариационном ряду, средняя арифметическая (![]() ) определяется как:
) определяется как:
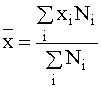 ,
,
т. е. в качестве веса при усреднении берётся частота Ni, соответствующая групповым значениям xi. Если ряд дискретный, то каждое значение признака представлено. Если же ряд интервальный, то его нужно превратить в условно дискретный: в качестве группового значения xi для каждого интервала вычисляется его середина.
Медиана (Ме[x]) - это такое значение признака, которое делит объём совокупности пополам в том смысле, что число элементов совокупности с индивидуальными значениями признака, меньшими медианы, равна числу элементов совокупности с индивидуальными значениями больше медианы.
Численное значение медианы можно определить по ряду накопленных частот. Накопленная частота для Ме[х] равна половине объёма совокупности (F(Me[x]) = N/2); имея ряд накопленных частот, можно вычислить, при каком значении признака накопленная частота равна половине объёма совокупности. Для интервального ряда в этом случае определяется только интервал, в котором будет находиться Ме[x], само значение приближённо можно определить как:
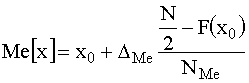 ,
,
где ![]() - начало интервала, содержащего медиану;
- начало интервала, содержащего медиану;
![]() - величина интервала, содержащего медиану;
- величина интервала, содержащего медиану;
![]() - накопленная частота на начало интервала, содержащего медиану;
- накопленная частота на начало интервала, содержащего медиану;
N - объём совокупности;
![]() - частота того интервала, в котором расположена медиана.
- частота того интервала, в котором расположена медиана.
Квартили (Q1, Q2, Q3) - значения признака, делящие упорядоченную по значению признака совокупность на 4 равные части. 1-ая квартиль (Q1) определяет такое значение признака, что ¼ единиц совокупности имеют значения признака меньше, чем Q1, а ¾ - значения больше чем Q1. 2-ая квартиль (Q2) равна медиане. 3-я квартиль (Q3) определяет такое значение признака, что ¾ единиц совокупности имеют значения признака меньше, чем Q3, а ¼ - больше чем Q3. Значения квартилей для сгруппированных данных определяются по накопленным частотам. При этом для 1-ой квартили накопленная частота сравнивается с величиной N·1/4; для 3-ей квартили - с величиной N·3/4. Значение квартили для интервального ряда распределения может быть уточнено по формуле:
![]() ,
,
![]() - нижняя граница интервала, в котором находится i-ая квантиль;
- нижняя граница интервала, в котором находится i-ая квантиль;
![]() - сумма накопленных частот интервалов, предшествующих интервалу, в котором находится i-ая квантиль;
- сумма накопленных частот интервалов, предшествующих интервалу, в котором находится i-ая квантиль;
![]() - частота интервала, в котором находится i-ая квантиль.
- частота интервала, в котором находится i-ая квантиль.
Децили (![]() ) - значения признака, делящие упорядоченную по значению признака совокупность на 10 равных частей.
) - значения признака, делящие упорядоченную по значению признака совокупность на 10 равных частей.
Мода (Мо[x]) - наиболее часто встречающееся значение признака в совокупности.
Для дискретного ряда — это то значение, которому соответствует наибольшая частота распределения. Для интервального ряда в начале определяется интервал, содержащий моду, - тот, которому соответствует наибольшая плотность распределения. Затем приближённо определяется численное значение моды.
Если ряд равноинтервальный, то используется формула
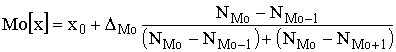 ,
,
где ![]() - начало интервала, содержащего моду,
- начало интервала, содержащего моду,
![]() - величина интервала, содержащего моду,
- величина интервала, содержащего моду,
![]() - частота того интервала, в котором расположена мода,
- частота того интервала, в котором расположена мода,
![]() -частота интервала, предшествующего модальному,
-частота интервала, предшествующего модальному,
![]() -частота интервала, следующего за модальным.
-частота интервала, следующего за модальным.
Средняя величина характеризует только уровень, закономерный для данной совокупности. В ряде случаев одно и то же численное значение средней может характеризовать совершенно различные совокупности. Поэтому для того чтобы судить о типичности средней для данной совокупности, её следует дополнить показателями, характеризующими вариацию (колеблемость) признака. Наиболее распространёнными из них являются дисперсия, среднее квадратичное отклонение, коэффициент вариации.
Дисперсия (![]() )- это среднее из квадратов отклонений от средней величины, для вариационного ряда она определяется по формуле
)- это среднее из квадратов отклонений от средней величины, для вариационного ряда она определяется по формуле
![]() = ------- ,
= ------- ,
Если ряд интервальный, то в качестве варианты (![]() ), также как при расчете средней, берётся середина интервала.
), также как при расчете средней, берётся середина интервала.
При использовании калькулятора, а также для дискретных рядов распределения более удобной может быть другая формула вычисления дисперсии:
![]() ,
,
где 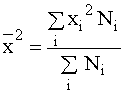 .
.
Наиболее широко в статистике применяется такой показатель вариации, как среднее квадратичное отклонение (![]() ), который представляет собой квадратный корень из дисперсии.
), который представляет собой квадратный корень из дисперсии.
Относительным показателем колеблемости признака в данной совокупности, является коэффициент вариации (V):
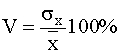 .
.
Коэффициент вариации позволяет сравнивать вариации различных признаков, а также одноименных признаков в разных совокупностях.
Теорема о разложении дисперсии при группировании.
Допустим при группировке совокупности по некоторому признаку Y (осуществленной каким угодно способом) было образовано К групп. Теорема о разложении дисперсии говорит, что общая дисперсия Y (по совокупности в целом) ![]() может быть разложена на две составные части: 1) межгрупповую и 2) среднюю из внутригрупповых
может быть разложена на две составные части: 1) межгрупповую и 2) среднюю из внутригрупповых ![]() дисперсии, а именно:
дисперсии, а именно:
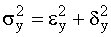 .
.
Межгрупповая дисперсия характеризует ту часть общей вариации (дисперсии) Y, которая обусловлена делением совокупности на группы. Она равна среднему квадрату отклонений групповых (частных) средних ![]() от общей средней
от общей средней ![]() :
:
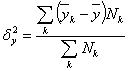 ,
,
где ![]() - среднее групповое среднее k-й группы.
- среднее групповое среднее k-й группы.

|
Из за большого объема эта статья размещена на нескольких страницах:
1 2 3 4 5 6 7 8 9 |




