Министерство образования  и  науки  Российской  Федерации

  НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ

  УНИВЕРСИТЕТ

  Э. Г. СОСНИНА

  ЧИСЛОВЫЕ  И ФУНКЦИОНАЛЬНЫЕ  РЯДЫ 

  Конспект лекций по математическому анализу

для студентов I курса  факультета Бизнеса экономической специальности

  НОВОСИБИРСК

  2014 

  I.  ЧИСЛОВЫЕ РЯДЫ

  --------------------------------------

1. Определение числового ряда.  Сходимость ряда.

Свойства сходящихся рядов.

  Пусть задана бесконечная последовательность чисел

  Определение 1. Числовым рядом называется сумма

а члены последовательности    называются членами ряда.

  Чтобы задать числовой ряд, необходимо задать члены ряда как функцию номера  . В этом случае  называется общим  членом ряда.

  Приведём примеры числовых рядов:

1) Гармонический ряд: 

2) Геометрическая прогрессия:

3)

  Определение 2.  Сумма n первых членов ряда называется  n—ой частичной суммой ряда и обозначается символом :

Очевидно, частичные суммы ряда образуют бесконечную последовательность    .

  Определение 3. Числовой ряд называется сходящимся, если существует конечный предел  последовательности    частичных сумм ряда, т. е.

Значение  S  этого предела называется суммой ряда.

  Рассмотрим примеры сходящихся рядов.

Пример 1.

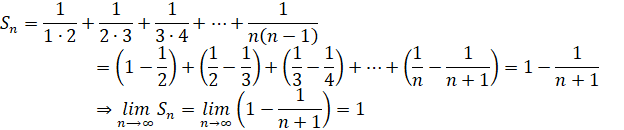
  Таким образом, ряд сходится  и его сумма .

Пример 2. Исследуем на сходимость геометрическую прогрессию

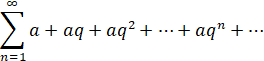
1)

2)

3)

4) .

Таким образом, геометрическая прогрессия сходится только в том случае, если знаменатель прогрессии  удовлетворяет условию  . При этом 

сумма прогрессии   .

  Остаток числового ряда

  ===================

Пусть задан числовой ряд

  Определение 4.Остатком числового ряда  называется ряд

  Теорема 1. Если ряд сходится, то его остаток  при .

  Доказательство

  Очевидно, что

Так как это равенство справедливо  при любом  n, то можно в нём перейти к пределу при :

Но для сходящегося ряда , откуда следует, что

  ( доказано).

  Определение 5. Числовой ряд называется расходящимся, если  предел последовательности частичных сумм ряда равен бесконечности или не существует. 


  Свойства сходящихся рядов

  Свойство 1. Отбрасывание конечного числа первых членов ряда не сказывается на его сходимости, т. е. ряды  и  

сходятся и расходятся одновременно.

  Свойство 2. Общий множитель членов ряда можно выносить за знак суммы, т. е..

  Свойство 3.Сходящиеся ряды можно почленно складывать, т. е.,если и , то .

  Свойство 4. Если в сходящемся ряде  объединить соседние члены в группы,

не изменяя порядка членов, и найти суммы этих групп, то ряд, составленный из полученных сумм, будет также сходится, причём к той же сумме, что и исходный ряд.

  Это свойство называется ассоциативностью ряда.

  Необходимый признак сходимости ряда

Теорема 2. Если ряд сходится, то его общий член стремиться к нулю.

  Доказательство

  Пусть ряд   сходится. Тогда . Очевидно,

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4