Теорема 2 .(Признак сходимости Лейбница ) Знакочередующийся ряд сходится, если  модули его членов монотонно убывают  с возрастанием  n  и общий член стремится к нулю, т. е.

Доказательство

        Рассмотрим чётные частичные суммы ряда и сгруппируем в них члены двумя разными способами

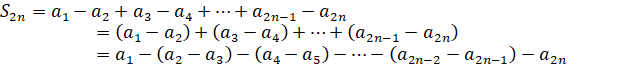
  Так как величины  убывают с возрастанием  n, то  из полученных

выражений для следует, что  последовательность монотонно возрастает с возрастанием n и ограничена сверху  .  Тогда по теореме Вейерштрасса эта последовательность имеет конечный предел:

Рассмотрим теперь нечётные частичные суммы ряда. Имеем

Таким образом, существует конечный предел частичных сумм ряда, а значит ряд сходится.

  Следствие 1. Сумма знакочередующегося ряда   не превышает  первого члена ряда.

  Следствие 2. Модуль остатка знакочередующегося ряда не превышает модуля первого отброшенного члена.

Свойства абсолютно и условно сходящихся рядов

  Сформулируем несколько теорем о свойстве коммутативности  рядов.

  Теорема 3. ( теорема Дирихле )  Если в сходящемся положительном ряде произвольным образом  переставить члены, то полученный ряд будет также сходится, а сумма его будет равна сумме исходного ряда.

  Это свойство ряда называется коммутативностью ряда.

  Теорема 4. Если в абсолютно сходящемся ряде  произвольным образом  переставить члены, то полученный ряд будет также абсолютно сходится, а его сумма будет равна сумме исходного ряда.

  Это обозначает, что абсолютно сходящийся ряд также обладает свойством коммутативности.

  Теорема 5. ( Теорема Римана ) Условно сходящийся ряд не обладает свойством коммутативности. Более того, каково бы ни было заданное число, можно так переставить члены условно сходящегося ряда, чтобы его сумма равнялась заданному числу.

  Такое различие свойств обусловлено принципиальной разницей между абсолютной и условной сходимостью рядов.

  Абсолютная сходимость ряда основана на быстром убывании членов ряда и потому не зависит от порядка членов.

  Условная сходимость ряда основана на взаимном погашении положительных и отрицательных членов и потому зависит от порядка расположения членов. 

  ФУНКЦИОНАЛЬНЫЕ РЯДЫ 

  Пусть задана последовательность функций , заданных на одном и том же множестве.

  Определение 1. Функциональным рядом называется выражение вида:

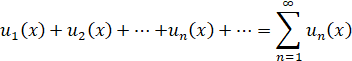
       Подставляя  в функциональный ряд вместо переменной  x некоторые её значения и т. д., мы получим различные числовые ряды ,

и т. д.. В зависимости от значения переменной x числовые ряды могут оказаться сходящимися или расходящимися.

  Определение 2. Совокупность всех значений переменной  x, для которых соответствующие числовые  ряды сходятся, называется областью сходимости функционального ряда.
        Сумма функционального ряда, таким образом, зависит от переменной  x  и следовательно является функцией, определённой в области сходимости ряда.

Поэтому можно ставить вопрос о её непрерывности, дифференцируемости, интегрируемости и т. д.

  СТЕПЕННЫЕ РЯДЫ

  Определение 2. Степенным рядом называется функциональный ряд, членами которого являются степенные функции.

  Таким образом, степенные ряды ---это ряды вида

  (1)

  (2)

  числа  ,  ,  ,  называются коэффициентами ряда.

  Очевидно, ряд (2) можно привести к ряду (1), если сделать подстановку

  . Поэтому в дальнейшем будем рассматривать ряды вида (1  Легко видеть, что степенной ряд сходится по крайней мере в одной точке 

Область сходимости степенных рядов достаточно просто находится с помощью теоремы Абеля. Мы приведем здесь формулировку этой теоремы в сокращённом виде и без доказательства.

  Терема Абеля. Если степенной ряд  сходится при некотором значении  , то он сходится абсолютно при всех значениях, для которых  .

  Если этот ряд расходится при некотором значении  , то он расходится  при всех значениях  , для которых 

  Интервал и радиус сходимости степенного ряда

  Из теоремы Абеля следует, что для любого степенного ряда существует  число  , удовлетворяющее условиям:  1) при всех значениях  , для которых  , ряд сходится абсолютно ;  2) при всех значениях  , для которых  , ряд расходится.

  Это число называется радиусом сходимости степенного ряда.

Если степенной ряд сходится только в одной точке  , то  .

Если степенной ряд сходится для любого  , то  .

  Открытый промежуток  называется интервалом сходимости степенного ряда.

  Для нахождения радиуса и интервала сходимости степенного ряда можно

использовать признаки Коши и Даламбера. Но поскольку эти признаки применимы только для положительных рядов, нужно рассматривать ряд,

составленный из модулей членов данного степенного ряда.

  Получим фор мулу для вычисления радиуса сходимости степенного ряда

с помощью признака Даламбера:

  Для сходимости ряда необходимо, чтобы выполнялось неравенство

Следовательно, 

  Если использовать радикальный признак Коши, то для вычисления радиуса сходимости степенного ряда получим формулу

  Свойства степенных рядов 

  Сформулируем несколько свойств степенных рядов, которые в дальнейшем будут полезны при использовании рядов в различных приложениях.

  Свойство 1. Сумма степенного ряда является непрерывной на интервале сходимости ряда.

  Свойство 2. Степенной ряд внутри промежутка сходимости можно почленно интегрировать:

  Пусть  .  Тогда

  Свойство 3. Степенной ряд внутри промежутка сходимости можно сколько угодно раз почленно дифференцировать:

  РЯДЫ  ТЕЙЛОРА И МАКЛОРЕНА 

  Прежде чем вводить понятие ряда Тейлора, вспомним теорему,  относящуюся к дифференциальному исчислению.

  Теорема 1. Пусть функция  в некоторой окрестности  точки  и в самой точке  имеет непрерывные производные до (  ) – го порядка включительно. Тогда  для любого  из этой окрестности имеет место формула Тейлора

где остаточный член  может быть записан в форме Лагранжа

  Если функция  в точке  и в её окрестности имеет непрерывные производные всех порядков, то для неё можно записать формулу Тейлора для любого значения  . При  мы приходим к понятию ряда Тейлора

  Этот ряд называется рядом Тейлора для функции  . Но для того, чтобы функция  была суммой этого ряда, он должен сходится именно к  .  .

  Например, запишем формулу Тейлора для функции  при произвольном  :

  Однако ряд справа – геометрическая прогрессия и сходится при 

именно к данной функции. Если  , то ряд справа расходится и функция не является суммой ряда, хотя для данных значений  она определена.

  Ответ на вопрос, при каком условии ряд Тейлора для функции  сходится к этой функции, даёт следующая

  Теорема 2. Ряд Тейлора для функции  сходится к этой функции тогда и только тогда, когда остаточный член  в формуле Тейлора

для  стремится к нулю при  .

  Доказательство

  Запишем формулу Тейлора для функции  в виде

так как многочлен Тейлора  равен очевидно  n – ой частичной сумме

  ряда Тейлора для  .

  Перейдём в записанном равенстве к пределу при  :

  Пусть  ряд Тейлора сходится к функции  . Это значит, что

и равенство принимает вид  , откуда

следует, что  . 

  Пусть теперь  . В этом случае приходим к равенству

  . Следовательно, ряд Тейлора сходится к функции  . Теорема доказана.

  При исследовании поведения остаточного члена формулы Тейлора будет полезна следующая

  Теорема 3. Для того, чтобы остаточный член формулы Тейлора для функции  стремился к нулю при  , достаточно, чтобы функция  в точке  имела производные всех порядков, ограниченные одним и тем же числом.

  Теорема 4.( Единственность разложения функции в ряд Тейлора)

  Пусть функция  является суммой некоторого степенного ряда

Тогда этот ряд является рядом Тейлора для функции  , т. е.

  Доказательство

  Применяя к равенству  раз теорему о почленном дифференцировании степенного ряда, Найдём

Если в этом равенстве положить  , то получим

что и требовалось доказать.

  Разложение некоторых элементарных функций

  в ряды Маклорена

  Рядом Маклорена называют ряд Тейлора для случая 

  Используя полученные ранее формулы Маклорена, запишем ряды Маклорена для функций  ,  .  .

Можно показать, например с помощью признака Даламбера, что ряды Маклорена для функций  ,  и  сходятся для  всех значений  , поэтому их радиус сходимости  .

  Биномиальный ряд

  Биномиальным рядом называется ряд Маклорена для функции

  , где  любое вещественное число.

  С помощью признака Даламбера можно показать, что биномиальный ряд сходится для  , т. е. радиус сходимости биномиального ряда

  Частные случаи биномиального ряда

  Найдём  разложение в ряд Маклорена функции

Для этого в биномиальный ряд подставим  . Получим

  Таким образом, имеем

  Заменив в данном разложении  на  ,  найдём разложение в

ряд Маклорена для функции

  Если в первом разложении заменить  на  , то получим ряд Маклорена для функции

  Разложение некоторых функций в ряд Маклорена можно получить, используя теорему о почленном интегрировании степенных рядов. Применим этот метод,  для разложения в ряды Маклорена функций  и 

  Имеем

  Подставим в интеграл разложение функции  в рял  и проинтегрируем этот ряд почленно. Получим

  Следовательно, разложение функции  имеет вид

  Для разложения в  ряд Маклорена  функции  воспользуемся

равенством

  Подставим в интеграл разложение в ряд функции  и проинтегрируем этот ряд почленно. Получим

  Следовательно, ряд Маклорена для функции  имеет вид

  Легко проверить, что ряды для функций  и

сходятся, если  .

  Суммирование рядов

  Полученные разложения в ряды Маклорена элементарных функций и теоремы о дифференцировании и интегрировании степенных рядов в ряде случаев позволяют находить суммы некоторых функциональных и числовых рядов.  Например, найдём сумму  следующего ряда

  Это степенной ряд, который сходится ( как легко проверить) для  .  Продифференцируем ряд почленно:

  Мы получили геометрическую прогрессию, первый член которой  и знаменатель  . Так как  , то геометрическая прогрессия

сходится  к сумме

  Тогда

  Применение рядов в приближённых вычислениях

  Пример 1. Вычислить приближённо 

используя разложение в степенной ряд функции  и взяв четыре первых члена разложения. Оценить погрешность вычисления.

  Запишем ряд Маклорена для функции  и положим  . Получим абсолютно сходящийся знакочередующийся ряд

  По условию задачи  , т. е.

  Оценим погрешность вычислений. Так как полученный ряд  знакочередующийся, то его остаток не превышает по модулю первого отброшенного члена. Следовательно, абсолютная погрешность  определяется неравенством

  Таким образом, в приближённом равенстве  погрешность имеет место в четвёртом знаке дробной части.

  Пример 2. Вычислить приближённо  , разложив

подынтегральную функцию в ряд и взяв три члена разложения. Оценить погрешность вычисления.

  Получим разложение подынтегральной функции в степенной ряд, использовав разложение функции  :

  Проинтегрируем этот  ряд почленно:

  В результате получим абсолютно сходящийся знакочередующийся ряд

По условию

  Оценим погрешность вычисления. Как и в примере 1, абсолютная погрешность определяется неравенством

  Отсюда видно, что погрешность в приближённом значении интеграла

имеет место уже в третьем знаке дробной части, поэтому ответ запишем в виде

  --------------------------------------------------------------

  РЕКОМЕНДУЕМАЯ  ЛИТЕРАТУРА

1.   «Дифференциальное и интегральное исчисления», ч  II

2.   «Теория рядов»

3.   «Конспект лекций по высшей математике», ч. II/

  . 

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4