Замечание. Признак Даламбера целесообразно применять, если общий  член

ряда содержит множители вида  или .

Пример1. Исследовать на сходимость числовой ряд 

  Запишем

Вычислим

Так как полученный предел меньше единицы, то делаем вывод: данный ряд сходится.

  Радикальный признак Коши

  Пусть для ряда  с положительными членами существует .

  Тогда  ряд сходится  при  и расходится при . Если ,

то признак неприменим.

  Пример 2.Исследовать на сходимость числовой ряд .

Для исследования ряда на сходимость применим радикальный признак Коши. Вычислим

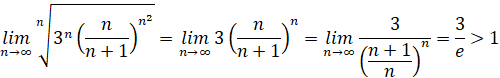
        Так как полученный предел больше единицы, то  делаем вывод: ряд расходится.

  Интегральный признак сходимости Коши

  Прежде чем формулировать сам признак, сделаем некоторые пояснения.

Пусть задан числовой ряд. Ранее уже было отмечено, что каждый член ряда

можно рассматривать, как значения некоторой функции f(n) от номера n члена  ряда

        Понятно, что можно ввести некоторую функцию f(x), которая была бы определена при всех значениях аргумента  x, больших единицы, а  при натуральных значениях аргумента совпадала бы со значениями членов ряда.

  Например, для гармонического ряда   такой функцией может

быть ;  для ряда  ----   и т. д.

А теперь сформулируем  собственно интегральный признак Коши.

  Пусть члены числового ряда  положительны и не возрастают

Пусть, далее,  f(x) ---функция, которая определена  для всех вещественных , непрерывна и удовлетворяет условию

        Тогда для сходимости ряда необходимо и достаточно, чтобы сходился несобственный интеграл  .

  Применим интегральный признак Коши для исследования сходимости

числового ряда  . Рассмотрим .  Ранее было показано, что этот интеграл сходится для  и расходится для . Следовательно, данный ряд также сходится для    и расходится для .

       

Знакопеременные и знакочередующиеся ряды

Определение 1. Числовой ряд называется знакопеременным, если он содержит бесконечное число как положительных, так и отрицательных членов.

  Например, знакопеременным является следующий числовой ряд

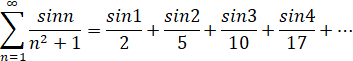
Рассмотрим  два ряда:

  (1)    ------ знакочередующийся ряд  и

  (2)    ------  положительный ряд, составленный из модулей

знакопеременного ряда.

  Определение 2. Знакопеременный ряд (1) называется абсолютно сходящимся,  если сходится ряд (2), составленный из модулей  членов  знакопеременного ряда (1).

  Определение 3. Знакопеременный ряд называется условно сходящимся,

если сам ряд сходится, а ряд, составленный из модулей его членов, расходится.

  Теорема 1. Если сходится ряд, составленный из модулей знакопеременного ряда, то сходится и сам знакопеременный ряд.

  Доказательство.

  Пусть дан знакопеременный ряд

(1)  , 

который абсолютно сходится. Это значит, что сходится ряд  (2)

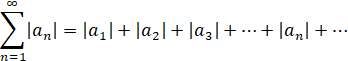
Тогда по свойству 2 об умножении сходящихся рядов сходится также ряд (3)

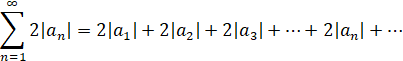
Очевидно, что для любого n выполняется неравенство

Следовательно, по первому признаку сравнения рядов сходится ряд

(4)  .Но тогда по свойству 3 о сложении и вычитании  рядов сходится ряд, членами которого являются разности членов рядов

(4) и (2), то есть заданный  знакопеременный ряд (1). 

        Для исследования знакопеременных рядов на абсолютную сходимость можно использовать все рассмотренные выше признаки сходимости положительных рядов.  Гораздо сложнее исследовать эти ряды на условную сходимость.

Знакочередующиеся ряды

  Определение 4. Знакопеременный ряд называется знакочередующимся, если соседние его члены имеют противоположные знаки.

       

       Знакочередующийся ряд принято записывать в виде:

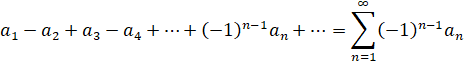
        Для знакочередующихся рядов имеется достаточно общий и практичный признак сходимости, принадлежащий Лейбницу.

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4