Статистический контроль качества продукции транспортного предприятия (стр. 2 )

3)  обеспечивают наглядность изображения динамики изменения качества продукции и настроенности процесса производства, что позволяет своевременно принимать меры к предупреждению брака не только контролерам, но и работникам цеха − рабочим, бригадирам, технологам, наладчикам, мастерам на стадии производства.

Статистические методы управления качеством продукции и услуг предполагают:

1) статистический анализ точности выполнения технологического процесса с целью приведения его к требуемой настроенности, точности и статистически устойчивому состоянию;

2) текущий контроль с целью регулирования и поддержания процесса в состоянии, обеспечивающем заданные качественные параметры;

3) выборочный статистический приемочный контроль качества готовой продукции.

Статистический анализ точности выполнения технологических процессов представляет собой единовременное обследование надежности процесса путем изучения качественных характеристик большого числа изделий, обработанных в определенных условиях на данной операции. Этот вид анализа дает возможность определить фактическую точность процесса и сравнить ее с заданной, оценить качество и устойчивость настроенности процесса, выявить вероятный процент дефектов, определить экономически целесообразные допуски.

Наиболее распространенными методами статистического анализа точности технологических процессов являются:

·  сравнение средних значений параметров с номинальными;

·  сравнение дисперсий;

·  оценка коэффициентов корреляции;

·  регрессионный анализ и др.

Метод сравнения средних значений параметров с номинальными используется в тех случаях, когда необходимо установить соответствие изготовляемого изделия эталону и в других случаях при сравнении значений одноименных показателей качества у нескольких групп изделий.

Метод сравнения дисперсий используется в случаях, когда требуется сделать характеристику изменчивости показателей качества, их рассеивание в зависимости от способа обработки или других факторов.

Коэффициент корреляции используется при оценке степени зависимости показателей качества от других показателей.

К регрессионному анализу прибегают в случаях оценки показателя качества по результатам наблюдений за другими показателями.

Статистическое регулирование технологического процесса представляет собой корректировку значений параметров технологического процесса по результатам выборочного контроля параметров выпускаемой продукции с целью обеспечения требуемого уровня качества. В процессе статистического регулирования технологического процесса периодически проверяют небольшое количество (5–10 единиц) изготовляемой продукции на конкретной операции, рассчитывают соответствующий распределению статистический параметр качества и сопоставляют с его номинальным значением. Этот контроль обеспечивает непрерывное наблюдение за стабильностью операции, однородностью качества, что дает возможность своевременно сигнализировать о наступающем отклонении и тем самым предупреждать возникновение дефектов и брака, обеспечивая заданный уровень качества продукции.

Распределение качественного параметра можно представить в виде кривой нормального распределения (рисунок 1), подчиненной закону нормального распределения случайных величин:

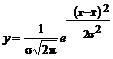, (1)

где y – плотность вероятностей или частота появления случайной переменной;

х – значение случайной переменной;

– центр распределения (группирование) отклонений, при котором значение у наибольшее;

– среднеквадратическое отклонение случайной переменной х.

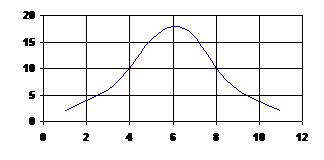
Рисунок 1– Кривая нормального распределения случайных величин

Приведем наиболее важные статистические характеристики закона нормального распределения:

1) среднее арифметическое значение качественного признака, характеризующее точность процесса,

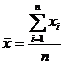, (2)

где п − количество единиц изделий в выборке (число замеров);

хi − замер контролируемого параметра i-го изделия в выборке;

2) среднеквадратическое отклонение случайной величины (значение качественного параметра, характеризующее величину поля фактического рассеивания размеров контролируемого параметра),

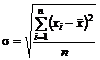; (3)

3) размах рассеивания качественной характеристики R, который представляет собой разность между наибольшими и наименьшими фактическими размерами,

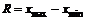. (4)

Результаты контроля (расчет приведенных характеристик) изображаются графически на карте статистического контроля (рисунок 2). Исходя из полученных параметров осуществляется управление процессом и принимаются решения о качестве продукции, выпущенной за период между двумя выборками.

Рисунок 2– Карта статистического контроля качества конденсаторов

Контрольная карта предназначена для статистического контроля по одному показателю качества. В ее верхней части отмечаются точками значения средних арифметических показателей качества х. Здесь нанесены четыре границы: две внешние, ограничивающие поле допуска, − Тв (верхний технический допуск) и Тн (нижний технический допуск), за пределами которых находится зона брака, и две внутренние − Рв (верхний предупредительный допуск) и Рн (нижний предупредительный допуск), между которыми находится номинальный размер контролируемого параметра Рном.

Внешние границы Тв и Тн определяются исходя из допустимой относительной величины отклонения контролируемого параметра от номинальной величины:

Тв = хном + ∆хф; (5)

Тн = хном − ∆хф, (6)

где ±∆хф − допустимая абсолютная величина отклонения от номинального размера,

, (7)

где – допустимая величина отклонения от номинальной величины, %.

Внутренние границы и определяются по формулам:

; , (8)

где – поле допуска на величину изучаемого параметра (по нижнему и

верхнему пределам от номинала);

п – количество единиц изделия в выборке.

Среднеарифметическая величина изучаемого параметра в j-й выборке

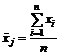, (9)

где хi – значение контролируемого параметра i-го изучения в j-й выборке.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6