Задачи корреляционного анализа сводятся к измерению тесноты известной связи между варьирующими признаками, определению причинных связей и оценки факторов, оказывающих наибольшее влияние на результативный признак.

Задачами регрессионного анализа является выбор типа модели (формы связи0, установление степени влияния независимых переменных на зависимую и определение расчетных значений зависимой переменной (функции регрессии).

Доходы бюджета выбраны в качестве независимой переменной х. Сопоставление данных параллельных рядов признаков х и у (табл. 2.3), показывает, что с возрастание признака х (доходы бюджета), растет, хотя и не всегда, результативный признак (расходы бюджета).

Строим таблицу по исходным данным.

Таблица 2.3

Распределение субъектов РФ по доходам и расходам гос. Бюджета

№

х

у

х2

у2

ху

у

1

4,2

5,4

17,64

29,16

22,68

5,60

2

3,8

5,2

14,44

27,04

19,76

5,22

3

6,4

8,7

40,96

75,69

55,68

7,71

4

2,1

3,2

4,41

10,24

6,72

3,59

5

2,4

4,6

5,76

21,16

11,04

3,87

6

2

3,5

4

12,25

7

3,49

7

0,7

2

0,49

4

1,4

2,24

8

3,9

5

15,21

25

19,5

5,31

9

8

7,4

64

54,76

59,2

9,25

10

4,2

6

17,64

36

25,2

5,60

11

2,5

4,6

6,25

21,16

11,5

3,97

12

3,9

4,9

15,21

24,01

19,11

5,31

13

7,6

8,6

57,76

73,96

65,36

8,87

14

4,1

5,8

16,81

33,64

23,78

5,51

15

0,5

1,8

0,25

3,24

0,9

2,05

16

1,2

3,1

1,44

9,61

3,72

2,72

17

3,6

4,5

12,96

20,25

16,2

5,03

18

2,2

3,8

4,84

14,44

8,36

3,68

19

0,9

1,9

0,81

3,61

1,71

2,43

20

2,3

3,1

5,29

9,61

7,13

3,78

21

3,5

4,6

12,25

21,16

16,1

4,93

22

4,4

6,2

19,36

38,44

27,28

5,79

23

4,8

7,2

23,04

51,84

34,56

6,18

24

7,5

8

56,25

64

60

8,77

25

0,8

1,7

0,64

2,89

1,36

2,34

26

3,5

4,7

12,25

22,09

16,45

4,93

27

4,1

6,5

16,81

42,25

26,65

5,51

28

6,3

8,6

39,69

73,96

54,18

7,62

29

5,3

6,8

28,09

46,24

36,04

6,66

30

5,2

7,1

27,04

50,41

36,92

6,56

Итого

111,9

154,5

541,59

922,11

695,49

154,52

Простое линейное уравнение регрессии:

(2.8) где у ─ теоретические расчетные значения результативного признака, полученные по уравнению регрессии; , ─ неизвестные параметры уравнения регрессии. ─ экономического смысла не имеет, ─ коэффициент регрессии, показывает изменение результативного признака при изменении факторного на 1; х ─ доходы бюджета, млн. руб.

Пользуясь расчетными значениями (табл. 2.2), исчислим параметры для данного уравнения регрессии:

;

;

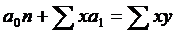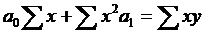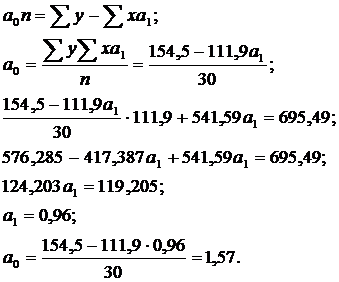
Следовательно, регрессионная модель распределения регионов по доходам бюджета для данного примера может быть записана в виде конкретного простого уравнения регрессии, по формуле 2.8:

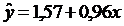
Расчетные значения , найденные по данному уравнению, приведены в табл. 2.2. Правильность расчета параметров уравнения регрессии может быть проверена сравнением сумм .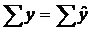

При линейной форме уравнения применяется показатель тесноты связи ─ линейный коэффициент корреляции:

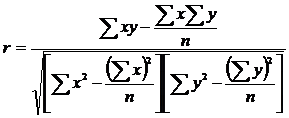(2.9)

Значение линейного коэффициента корреляции важно для исследования социально ─ экономических явлений и процессов, распределение которых близко к нормальному. Он принимает значения в интервале: -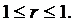

Отрицательные значения указывают на обратную связь, положительные ─ на прямую. При r=0 линейная связь отсутствует. Чем ближе коэффициента корреляции по абсолютной величине к единице, тем теснее связь между признаками. И при r= связь ─функциональная.

Используя данные табл.2.2 рассчитаем линейный коэффициент корреляции по формуле (2.9):

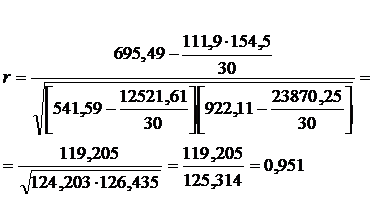
Т. к. коэффициент корреляции (r = 0,951) близок к единице, значит связь между признаками тесная, прямая.

Задание 3

По результатам выполнения задания 1 с вероятностью 0,683 определите:

1.  Ошибку выборки среднего дохода бюджета и границы, в которых он будет находиться в генеральной совокупности.

2.  Ошибку выборки доли регионов со средним доходом бюджета 5 млрд. руб. и более и границы, в которых будет находиться генеральная доля.

Решение.

Предельная ошибка выборки позволяет определить предельные значения характеристик генеральной совокупности и их доверительные интервалы:

для средней ; ; (2.10)

для доли ; . (2.11)

Это означает, что с заданной вероятностью можно утверждать, что значение генеральной средней следует ожидать в пределах от 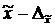до .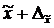

Аналогичным образом может быть записан доверительный интервал генеральной доли: ; .

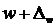1. При механическом отборе предельная ошибка выборки для средней определяется по формуле:

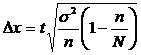, (2.12)

Где t ─ нормированное отклонение ─ «коэффициент доверия», зависящий от вероятности, с которой гарантируется предельная ошибка выборки; – генеральная дисперсия (дисперсия признака в генеральной совокупности) – это средняя арифметическая квадратов отклонений отдельных значений признака от их средней арифметической; – относительное число единиц.

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10