Государственный бюджет (стр. 5 )

Медианным является интервал, в котором сумма накопленных частностей превысит половину общего числа наблюдений, т. е. 15.

Значение медианы вычисляется по формуле:

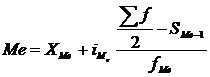, (2.3)

где − - нижняя граница медианного интервала,

- накопленная частота интервала, предшествующего медианному,

- величина интервала,

- частота медианного интервала.

- половина от общего числа наблюдений

Найдем медианный интервал. Таким интервалом будет интервал доходов бюджета регионов (3,5-5 млн. руб.), поскольку его накопленная частота равна 23 (11+7+5), что превышает половину суммы всех частот (30:2=15). Нижняя граница интервала 3,5 млн. руб.. его частота 11; частота накопленная до него, равна 12.

Подставив данные в формулу (2.3), получим, млн. руб.:

.

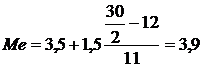Полученный результат говорит о том, что из 30 регионов 15 регионов имеют доходы бюджета менее 3 млн. руб., а 15 регионов − более.

3. Рассчитываем характеристику ряда распределения регионов. Если данные представлены в виде дискретных или интервальных рядов распределения, в которых одинаковые значения признака () объединены в группы, имеющие различное число единиц (), называемое частотой (весом), применяется средняя арифметическая взвешенная:

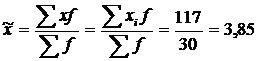(2.4)

где вес (частота повторения одинаковых признаков);

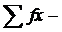сумма произведений величины признаков на их частоты;

общая численность единиц совокупности.

Таблица 2.1

Среднее квадратическое отклонение () представляет собой корень квадратный из дисперсии и рано:

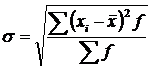- взвешенная. (2.5)

.

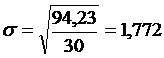Среднеквадратическое отклонение показывает, что значение признака в совокупности отклоняется от средней величины в ту или иную сторону в среднем на 1,772 млн. руб.

В отличие от дисперсии среднее квадратическое отклонение является абсолютной мерой вариации признака в совокупности и выражается в единицах измерения варьирующего признака.

Для сравнения размеров вариации различных признаков, а также для сравнения степени вариации одноименных признаков в нескольких совокупностях исчисляется коэффициент вариации (V), который представляет собой процентное отношение среднего квадратического отклонения и средней арифметической:

(2.6)

По величине коэффициента вариации можно судить о степени вариации признаков, а, следовательно, об однородности состава совокупности. Чем больше его величина, тем больше разброс значений признака вокруг средней, тем менее однородна совокупность по составу.

Вычислим коэффициент вариации по формуле (2.6):

.

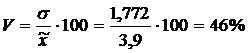Если коэффициент вариации выше 40%, значит вариация сильная, средняя величина плохо представляет всю совокупность, является нетипичной, ненадежной.

4. Средняя арифметическая простая равна сумме значений признака, деленной на их число:

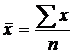, (2.7)

где – значение признака (вариант);

–число единиц признака.

Средняя арифметическая простая применяется в тех случаях, когда варианты представлены индивидуально в виде их перечня в любом порядке или в виде ранжированного ряда.

Вычислим среднюю арифметическую простую по формуле (2.7):

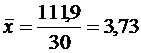
Задание 2

Связь между признаками – доходы и расходы бюджета.

Установить связь между признаками.

1. Аналитическая группировка позволяет изучать взаимосвязь факторного и результативно признаков.

Основные этапы проведения аналитической группировки – обоснование и выбор факторного и результативного признаков, подсчет числа единиц в каждой из образованных групп, определение объема варьирующих признаков в пределах созданных групп, а также исчисление средних размеров результативного показателя. Результаты группировки оформляют в таблице 2.2

Таблица 2.2

Группировка регионов по доходам бюджета

2. Корреляционно-регрессионный анализ.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10