2)Магнус . Начальный курс: Учеб. - М.:Дело, 2004, с. 264-350.
3) Елисеева по эконометрике: Учебное пособие.- М.: Финансы и статистика, 2004, с. 137-163.
Тема: Структурная и приведенная формы модели
План:
1)Системы уравнений, используемых в эконометрике.
2)Внешне не связанные уравнения.
3)Структурная и приведенная формы моделей.
4)Примеры систем одновременных уравнений.
Литература:
1)Елисеева : Учебник - М.: Финансы и статистика, 2004, с. 177-225.
2)Магнус . Начальный курс: Учеб. - М.:Дело, 2004, с. 220-241.
3) Елисеева по эконометрике: Учебное пособие.- М.: Финансы и статистика, 2004, с. 106-121.
Тема: Проблема идентификации
План:
1)Проблема идентификации при переходе от приведенной формы к структурной.
2)Оценивание параметров структурной модели.
3)Косвенный метод наименьших квадратов.
4)Двухшаговый метод наименьших квадратов.
5)Трехшаговый метод наименьших квадратов.
Литература:
1)Елисеева : Учебник - М.: Финансы и статистика, 2004, с. 185-225.
2)Магнус . Начальный курс: Учеб. - М.:Дело, 2004, с. 220-241.
3) Елисеева по эконометрике: Учебное пособие.- М.: Финансы и статистика, 2004, с. 106-121.
8. ТЕСТОВЫЕ ЗАДАНИЯ ДЛЯ САМОКОНТРОЛЯ И ИТОГОВОГО КОНТРОЛЯ
ТЕМА: Линейная парная регрессия и корреляция
1. Уравнение регрессии описывает:
1)функциональную зависимость между переменными;
2)статистическую зависимость между переменными;
3)корреляционную зависимость между переменными.
2. Парная регрессия используется, если:
1)имеется доминирующий фактор;
2)выявлены два значимых фактора;
3)между факторами прямая пропорциональная зависимость.
3. Графический метод выбора вида математической функции заключается:
1)в анализе теории изучаемой взаимосвязи;
2)в построении поля корреляции;
3)в сравнивании величины остаточной дисперсии для различных функций.
4. Случайная величина ![]() характеризует:
характеризует:
1)влияние учтенных в модели факторов;
2)фактическое значение результативного признака;
3)влияние не учтенных в модели факторов.
5. Параметры линейной регрессии оцениваются:
1)методом наименьших квадратов;
2)косвенным методом наименьших квадратов;
3)двухшаговым методом наименьших квадратов.
6. Параметр b уравнения парной линейной регрессии называется:
1)коэффициентом эластичности;
2)коэффициентом регрессии;
3)индексом детерминации.
7. Коэффициент регрессии показывает:
1)среднее изменение результата с изменением фактора на одну единицу;
2)на сколько процентов изменится в среднем результат, если фактор изменится на 1%;
3)среднее изменение результата с изменением фактора на 1%.
8. Метод наименьших квадратов позволяет получить такие оценки параметров, при которых:
1)параметры принимают положительные значения;
2)сумма квадратов отклонений фактических значений результативного признака от расчетных максимальна;
3)сумма квадратов отклонений фактических значений результативного признака от расчетных минимальна.
9. Линейный коэффициент корреляции находится в границах:
1)![]() ;
;
2)![]() ;
;
3)![]() .
.
10. Коэффициент детерминации характеризует:
1)качество подбора линейной функции;
2)долю дисперсии, вызванную влиянием не учтенных в модели факторов;
3)значимость линейный коэффициент корреляции.
Ключ к тесту:
№ вопроса | Вариант ответа | № вопроса | Вариант ответа |
1 | 2 | 6 | 2 |
2 | 1 | 7 | 1 |
3 | 2 | 8 | 3 |
4 | 3 | 9 | 3 |
5 | 1 | 10 | 1 |
ТЕМА: Нелинейная регрессия и корреляция
1. Примером нелинейной регрессии по включенным в нее объясняющим переменным служит функция:
1)степенная;
2)экспоненциальная;
3)равносторонняя гипербола.
2.Парабола второй степени целесообразна к применению, если:
1)для определенного интервала значений фактора меняется характер связи рассматриваемых признаков;
2)с увеличением значения фактора, значение результативного признака увеличивается;
3)для определенного интервала значений фактора не меняется характер связи рассматриваемых признаков.
3. При изучении эластичности спроса от цен используется:
1)линейная;
2)степенная;
3)экспоненциальная.
4. Нелинейная регрессия по включенным параметрам оценивается:
1)косвенным методом наименьших квадратов;
2)методом наименьших квадратов;
3)двухшаговым методом наименьших квадратов.
5. Параметр b в степенной функции является:
1)парным коэффициентом корреляции;
2)коэффициентом регрессии;
3)коэффициентом эластичности.
6. Зависимость спроса от цен характеризуется уравнением вида
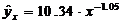 . Следовательно:
. Следовательно:
1)с увеличением цен на одну единицу спрос увеличивается на 10,34%;
2)с уменьшением цен на 1% спрос снижается на 10,34%;
3)с увеличением цен на 1% спрос снижается на 1,05%.
7. Индекс детерминации используется для оценки:
1)целесообразности включения фактора в уравнение регрессии;
2)существенности в целом уравнения нелинейной регрессии;
3)значимости показателя тесноты связи.
8. Допустимый предел значения средней ошибки аппроксимации:
1)не более 8-10%;
2)не менее 8-10%;
3)не более 10-20%;
9. Статистическая значимость коэффициентов регрессии и корреляции оценивается по:
1)t-критерию Стьюдента;
2)F-критерию Фишера;
3)среднему коэффициенту эластичности.
10. Индекс корреляции для нелинейной регрессии находится в границах:
1)![]() ;
;
2)![]() ;
;
3)![]() .
.
Ключ к тесту:
№ вопроса | Вариант ответа | № вопроса | Вариант ответа |
1 | 3 | 6 | 3 |
2 | 1 | 7 | 2 |
3 | 2 | 8 | 1 |
4 | 2 | 9 | 1 |
5 | 3 | 10 | 3 |
ТЕМА: Множественная регрессия и корреляция
1.Множественная регрессия используется, если:
1)между факторами существуют нелинейные соотношения;
2)в уравнение необходимо включить два и более фактора;
3)имеется доминирующий фактор.
2. Факторы, включаемые во множественную регрессию, должны быть:
1)мультиколлинеарны;
2)интеркоррелированы;
3)количественно измеримы.
3. В линейной множественной регрессии параметры при x называются:
1)коэффициентами «чистой» регрессии;
2)коэффициентами эластичности;
3)коэффициентами аппроксимации.
4. Зависимость расходов на продукты питания (y, тыс. руб.) от месячного дохода на одного члена семьи (![]() , тыс. руб.) и размера семьи (
, тыс. руб.) и размера семьи (![]() , человек) характеризуется уравнением
, человек) характеризуется уравнением ![]() . Следовательно:
. Следовательно:
1)с ростом дохода на одного члени семьи на 1 тыс. руб. расходы на питание возрастут в среднем на 0,32 тыс. руб. при том же среднем размере семьи;
2)с ростом дохода на одного члени семьи на 1 тыс. руб. расходы на питание возрастут в среднем на 0,81 тыс. руб. при том же среднем размере семьи;
3)с ростом дохода на одного члени семьи на 1 тыс. руб. расходы на питание возрастут в среднем на 0,6 тыс. руб. при том же среднем размере семьи;
5. При исследовании спроса на мясо (y) от цены (![]() ) и дохода (
) и дохода (![]() ) получено уравнение
) получено уравнение 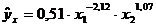
 . Следовательно:
. Следовательно:
1)рост цен на 1% при том же доходе вызывает увеличение спроса в среднем на 0,51%;
2)рост цен на 1% при том же доходе вызывает увеличение спроса в среднем на 1,07%;
3)рост цен на 1% при том же доходе вызывает снижение спроса в среднем на 2,12%;
6. Параметры уравнения множественной регрессии оцениваются:
1)двухшаговым методом наименьших квадратов;
2)косвенным методом наименьших квадратов;
3)методом наименьших квадратов.
7. Относительная сила влияния факторов на результативный признак оценивается:
1)индексом множественной корреляции;
2)частными коэффициентами эластичности;
3)параметрами b при независимых переменных.
8. Частный коэффициент корреляции первого порядка ![]() показывает:
показывает:
1)корреляцию y и фактора ![]() при закреплении фактора
при закреплении фактора ![]() на постоянном уровне;
на постоянном уровне;
2)корреляцию y и фактора ![]() при закреплении фактора
при закреплении фактора ![]() на постоянном уровне;
на постоянном уровне;
3)совокупное действие факторов ![]() и
и ![]() на результативный признак.
на результативный признак.
9. Значимость уравнения множественной регрессии в целом оценивается по:
1)F-критерию Фишера;
2)t-критерию Стьюдента;
3)частному F-критерию Фишера.
10. Факторы, имеющие два или более качественных уровней, включаемые в уравнение множественной регрессии, называются:
1)фиктивными переменными;
2)объясняющими переменными;
3)объясняемыми переменными.
Ключ к тесту:
№ вопроса | Вариант ответа | № вопроса | Вариант ответа |
1 | 2 | 6 | 3 |
2 | 3 | 7 | 2 |
3 | 1 | 8 | 2 |
4 | 1 | 9 | 1 |
5 | 3 | 10 | 1 |

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 |




