Учебно-методические рекомендации для студентов факультета заочного обучения 1 курса (3, 5-летний срок обучения) по дисциплине: математика (стр. 5 )

u

j(u)

u

j(u)

u

j(u)

u

j(u)

0,0

0,3989

1,0

0,2420

2,0

0,0540

3,0

0,0044

0,1

0,3970

1,1

0,2179

2,1

0,0440

3,1

0,0033

0,2

0,3910

1,2

0,1942

2,2

0,0355

3,2

0,0024

0,3

0,3814

1,3

0,1714

2,3

0,0283

3,3

0,0017

0,4

0,3683

1,4

0,1497

2,4

0,0224

3,4

0,0012

0,5

0,3521

1,5

0,1295

2,5

0,0175

3,5

0,0009

0,6

0,3332

1,6

0,1109

2,6

0,0136

3,6

0,0006

0,7

0,3123

1,7

0,0940

2,7

0,0104

3,7

0,0004

0,8

0,2897

1,8

0,0790

2,8

0,0079

3,8

0,0003

0,9

0,2661

1,9

0,0656

2,9

0,0060

3,9

0,0002

Уровень значимости a для двусторонней критической области

n

0,1

0,05

0,01

0,001

n

0,1

0,05

0,01

0,001

1

6 ,313

12 ,71

63 ,656

636 ,62

16

1 ,745

2 ,119

2 ,921

4 ,015

2

2 ,919

4 ,302

9 ,925

31 ,599

17

1 ,739

2 ,109

2 ,898

3 ,965

3

2 ,353

3 ,182

5 ,841

12 ,924

18

1 ,734

2 ,101

2 ,878

3 ,921

4

2 ,131

2 ,776

4 ,604

8 ,610

19

1 ,729

2 ,093

2 ,861

3 ,883

5

2 ,015

2 ,570

4 ,032

6 ,869

20

1 ,725

2 ,086

2 ,845

3 ,849

6

1 ,943

2 ,446

3 ,707

5 ,959

21

1 ,721

2 ,079

2 ,831

3 ,819

7

1 ,894

2 ,364

3 ,499

5 ,408

22

1 ,717

2 ,074

2 ,818

3 ,792

8

1 ,859

2 ,306

3 ,355

5 ,041

23

1 ,714

2 ,068

2 ,807

3 ,767

9

1 ,833

2 ,262

3 ,249

4 ,781

24

1 ,711

2 ,064

2 ,797

3 ,745

10

1 ,812

2 ,228

3 ,169

4 ,587

25

1 ,708

2 ,059

2 ,785

3 ,725

11

1 ,795

2 ,201

3 ,106

4 ,437

26

1 ,706

2 ,055

2 ,778

3 ,707

12

1 ,782

2 ,179

3 ,054

4 ,318

27

1 ,703

2 ,052

2 ,770

3 ,689

13

1 ,771

2 ,160

3 ,012

4 ,221

28

1 ,701

2 ,048

2 ,763

3 ,674

14

1 ,761

2 ,145

2 ,977

4 ,140

29

1 ,699

2 ,045

2 ,756

3 ,659

15

1 ,753

2 ,131

2 ,946

4 ,073

30

1 ,697

2 ,042

2 ,750

3 ,646

:

1 ,644

1 ,959

2 ,576

3 ,290

0,9

0,95

0,99

0,999

0,9

0,95

0,99

0,999

Доверительная вероятность g

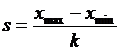
n

0

1

2

3

4

5

6

7

8

9

0

-

-

1,13

1,69

2,06

2,23

2,56

2,70

2,85

2,97

10

3,08

3,17

3,26

3,34

3,41

3,47

3,53

3,59

3,64

3,69

20

3,73

3,78

3,82

3,86

3,90

3,93

3,96

4,00

4,03

4,06

30

4,09

4,11

4,14

4,16

4,19

4,21

4,24

4,26

4,28

4,30

40

4,32

4,34

4,36

4,38

4,40

4,42

4,43

4,45

4,47

4,48

50

4,50

4,51

4,53

4,54

4,56

4,59

4,60

4,60

4,61

4,63

60

4,64

4,65

4,66

4,68

4,69

4,70

4,71

4,72

4,73

4,74

70

4,75

4,77

4,78

4,79

4,80

4,81

4,82

4,83

4,83

4,84

80

4,85

4,86

4,87

4,88

4,88

4,90

4,91

4,91

4,92

4,93

90

4,94

4,95

4,96

4,96

4,97

4,98

4,99

4,99

5,00

5,01

n

100

200

300

400

500

600

700

800

900

1000

k

5,02

5,49

5,76

5,94

6,07

6,18

6,28

6,35

6,42

6,48

n

Уровни значимости a

n

Уровни значимости a

0,05

0,01

0,001

0,05

0,01

0,001

3

0,9969

0,999

0,9999

26

0,388

0,496

0,607

4

0,950

0,9900

0,9990

27

0,381

0,487

0,597

5

0,878

0,9597

0,991

28

0,374

0,479

0,588

6

0,811

0,9172

0,9741

29

0,367

0,470

0,579

7

0,754

0,875

0,9509

30

0,361

0,463

0,570

8

0,707

0,834

0,9244

32

0,349

0,449

0,554

9

0,666

0,798

0,898

35

0,332

0,435

0,539

10

0,632

0,765

0,872

37

0,325

0,418

0,519

11

0,602

0,735

0,847

40

0,312

0,402

0,501

12

0,576

0,708

0,823

42

0,304

0,393

0,490

13

0,553

0,684

0,801

45

0,292

0,384

0,416

14

0,532

0,661

0,780

47

0,288

0,372

0,465

15

0,544

0,641

0,760

50

0,279

0,361

0,451

16

0,497

0,623

0,742

52

0,273

0,354

0,443

17

0,482

0,606

0,725

60

0,254

0,330

0,414

18

0,468

0,590

0,708

80

0,220

0,286

0,380

19

0,456

0,575

0,693

100

0,196

0,258

0,324

20

0,444

0,561

0,679

125

0,175

0,230

0,286

21

0,433

0,549

0,665

150

0,160

0,210

0,249

22

0,423

0,537

0,652

250

0,124

0,163

0,207

23

0,413

0,526

0,641

500

0,088

0,115

0,147

24

0,404

0,515

0,629

1000

0,062

0,081

0,104

25

0,396

0,505

0,618