Два студента решают задачу. Вероятность того, что задачу решит первый студент составляет 0,8, вероятность решения для второго студента 0,4. Найти вероятность того, что: а) задачу решит хотя бы один студент; б) задачу решит только один студент; в) задачу решат оба студента; г) задачу не решит ни один студент.
Решение:
Рассмотрим четыре элементарных события: А1 - задачу решил первый студент; `А1 - задачу не решил первый студент; А2 - задачу решил второй студент; `А2 - задачу не решил второй студент. Вероятности событий А1 и А2 известны из условия задачи. События `А1 и `А2 являются противоположными событиям А1 и А2, следовательно их вероятности можно найти по теореме о вероятности полной группы событий.
Р(А1) = 0,8 Р(`А1) = 1- 0,8 = 0,2
Р(А2) = 0,4 Р(`А2) = 1 - 0,4 = 0,6
а) Событие В - "задачу решит хотя бы один студент" является суммой двух совместных событий А1 и А2, то есть В = А1+А2. По формуле суммы совместных событий получим:
Р(В) = Р(А1+А2) = Р(А1) +Р(А2) - Р(А1× А2) = 0,8 + 0,4 - 0,8× 0,4 = 0,88
б) Событие С - "задачу решит только один студент" заключается в том, что решит только первый и не решит второй, или решит только второй и не решит первый студент. Сложное событие С можно представить в следующем виде:
С = А1×`А2 +`А1× А2
События (А1`А2) и (`А1 А2) несовместны, события А1 и `А2; `А1 и А2 независимы.
Р(С) = Р(А1) × Р(`А2) + Р(`А1) × Р(А2) = 0,8 × 0,6 + 0,2 × 0,4 = 0,56
в) Событие D – «задачу решат оба студента» является произведением независимых событий А1 и А2, то есть D = А1 × А2
Р(D) = Р(А1) × Р(А2) = 0,8 × 0,4 = 0,32
в) Событие Е – «задачу не решит ни один студент» является произведением независимых событий `А1 и `А2, то есть Е = `А1 × `А2
Р(Е) = Р(`А1) × Р(`А2) = 0,2 × 0,6 = 0,12
Задание 2.
По цели произведено три выстрела. Вероятность попадания при одном выстреле равна 0,8. Составить закон распределения вероятностей количества попаданий. Вычислить математическое ожидание М(Х), дисперсию D(Х), среднее квадратическое отклонение.
Решение:
Для определения вероятности того, что в серии из n испытаний событие А произойдет m раз воспользуемся формулой Бернулли.
Pn (m) = n!/(m!(n-m)!) pm qn-m
P3 (0) = 3! / (0! (3-0)!) 0,80 ×0,23 = (1× 2× 3 / 1×2×3) × 1× 0,008 = 0,008
P3 (1) = 3! / (1! (3-1)!) 0,81 ×0,22 = (1× 2× 3 / 1×1×2) × 0,8× 0,04 = 0,096
P3 (2) = 3! / (2! (3-2)!) 0,82 ×0,2 = (1× 2× 3 / 1×2×1) × 0,64× 0,2 = 0,384
P3 (3) = 3! / (3! (3-3)!) 0,83 = 1× 2× 3 / 1×1×2×3 × 0,512 = 0,512 (т. к. 0!=1)
Составим ряд распределения. Для этого укажем в таблице все возможные значения случайной величины и их вычисленные вероятности.
P(X=0) = 0,008; Р (Х=1) = 0,096; Р (Х=2) = 0,384; Р (Х=3) = 0,512
Х | 0 | 1 | 2 | 3 |
Р | 0,008 | 0,096 | 0,384 | 0,512 |
Проверка: 0,008+0,096+0,384+0,512=1
Математическое ожидание:
М(Х) = 0×0,008 + 1× 0,096 + 2× 0,384 + 3× 0,512 = 2,4
Дисперсия:
D(Х) = (0 - 2,4)2 ×0,008 + (1 - 2,4)2 ×0,096+(2 - 2,4)2 ×0,384+(3 - 2,4)2 ×0,512 = 0,48
Среднее квадратическое отклонение:
Задание 3.
Из генеральной совокупности извлечена следующая выборка.
35 38 33 32 35 36 39 36 37 34 35 35 36 34 37 36 38 37 35 33
Составить безынтервальный вариационный ряд. Построить полигон. Вычислить выборочное среднее значение, дисперсию, среднее квадратическое отклонение, коэффициент вариации, статистическую ошибку выборочной средней. Указать моду и медиану.
Решение:
Безынтервальный вариационный ряд:
х | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 |
m | 1 | 2 | 2 | 5 | 4 | 3 | 2 | 1 |
Вычисление статистических показателей (при помощи расчетной таблицы):
х | m | m х | х - `х | (х - `х)2 | m(х - `х)2 |
32 | 1 | 32 | -3,6 | 12,96 | 12,96 |
33 | 2 | 66 | -2,6 | 6,76 | 13,52 |
34 | 2 | 68 | -1,6 | 2,56 | 5,12 |
35 | 5 | 175 | -0,6 | 0,36 | 1,8 |
36 | 4 | 144 | 0,4 | 0,16 | 0,64 |
37 | 3 | 111 | 1,4 | 1,96 | 5,88 |
38 | 2 | 76 | 2,4 | 5,76 | 11,52 |
39 | 1 | 39 | 3,4 | 11,56 | 11,56 |
å | 20 | 711 | 63 |
Выборочное среднее `Х = å Хi / n `Х = 711/20 = 35,6
Дисперсия D = å m(Xi - `X)2 / n-1 D = 63/19 = 3,3
Выборочное среднее квадратическое отклонение
Коэффициент вариации V=1,8/35,6×100% = 5%
Статистическая ошибка выборочной средней m`X = 1,8/4,5 = 0,4
Мо = 35 (варианта, имеющая наибольшую частоту);
Ме = 36 (середина ранжированного ряда).
Задание 4.
У спортсменов контрольной (Х) и экспериментальной (У) групп измерены результаты в прыжке в высоту. С помощью t-критерия Стьюдента определите, являются ли различия уровня спортсменов подготовленности достоверными.
Х | 39 | 40 | 45 | 37 | 42 | 40 | 46 | 41 |
У | 41 | 39 | 42 | 48 | 47 | 44 | 41 |
Решение:
1. Вычислим средние значения показателей в обеих группах
`Х = (39+40+45+37+42+40+46+41)/8 = 41,2 см ≈ 41 см
`Y = (41+39+42+48+47+44+41)/ 7 = 43,1 см ≈ 43 см
2. Вычислим выборочные дисперсии sx2 и sy2
sx2 =9 см2
sy2 = 11,2 см2
Количество испытуемых в выборках: nx=8; ny=7, тогда количество степеней свободы n = 8+7-2 = 13
Найдем эмпирическое (выборочное) значение t-критерия Стьюдента
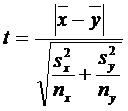
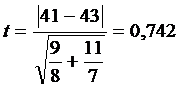
По таблице критических значений t-критерия Стьюдента определяем t0.05 = 2,160
Вывод: Так как вычисленное значение t-критерия оказалось меньше табличного (0,742 <2,160), то различия между выборочными средними не являются статистически достоверными.
Задание 5.
Установить тесноту взаимосвязи между показателями Х и У при помощи коэффициента корреляции Браве-Пирсона
Х | 12 | 15 | 11 | 14 | 13 |
У | 72 | 81 | 73 | 78 | 71 |
Решение:
Для вычисления коэффициента корреляции Браве-Пирсона составим расчетную таблицу, при помощи которой найдем выборочные средние`X,`Y, а также средние квадратические отклонения sx и sy.
№ | х | Y | х -`y | (х -`х)2 | y -`y | (y -`y)2 | (х -`х) (y -`y) |
1 | 12 | 72 | -1 | 1 | -3 | 9 | 3 |
2 | 15 | 81 | 2 | 4 | 6 | 36 | 12 |
3 | 11 | 73 | -2 | 4 | -2 | 4 | 4 |
4 | 14 | 78 | 1 | 1 | 3 | 9 | 3 |
5 | 13 | 71 | 0 | 0 | -4 | 16 | 0 |
S | 65 | 375 | 10 | 74 | 22 |
`х = 65/5 = 13; `у = 375/5 = 75;

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 |




