Учебно-методические рекомендации для студентов факультета заочного обучения 1 курса (3, 5-летний срок обучения) по дисциплине: математика (стр. 3 )

sx2 = 10/4 = 2,5; sx =1,6; sy2 = 74/4 = 18,5 sy= 4,3

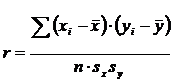
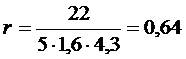
Для определения достоверности взаимосвязи необходимо сравнить полученный выборочный коэффициент корреляции с критическим значением (находится в статистической таблице), которое зависит от объема выборки. При объеме выборки n = 5 критическое значение rкр = 0,878. Поскольку выборочное значение оказалось меньше критического, то нельзя утверждать, что между показателями Х и Y существует взаимосвязь.

Задание 6.

Установить тесноту взаимосвязи между показателями Х и У при помощи коэффициента корреляции Спирмена.

Решение:

Составим расчетную таблицу, в первом столбце которой указаны номера испытуемых, во втором и третьем – экспериментальные показатели, в четвертом и пятом – ранги значений Х и Y, в шестом – разность рангов, в седьмом квадрат разности рангов.

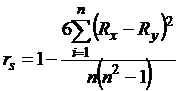
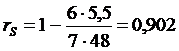
Критическое значение коэффициента корреляции при n = 7 и a = 0,05 составляет 0,754, выборочное значение коэффициента корреляции составляет 0,902. Поскольку выборочное значение коэффициента корреляции больше, чем критическое, можно утверждать, что между величинами Х и Y существует достоверная положительная взаимосвязь, вероятность ошибочности такого утверждение 0,05.

Задачи для самостоятельного решения

Задача 1.

В ящике находится 12 деталей, из которых 4 – бракованных. Сборщик наудачу вытаскивает три детали. Найти вероятность того следующих событий:

а) все детали – исправные;

б) все детали – бракованные;

в) две детали – исправные, одна - бракованная.

Задача 2.

Программа экзамена содержит 25 вопросов, из которых студент знает 20. В билете три вопроса. Найти вероятность того, что студент сможет ответить на все вопросы.

Задача 3.

В мешке 5 кубиков с буквами О, П, Р, С, Т. Найти вероятность того, что на вынутых по одному и расположенных в одну линию кубиках получится слово "СПОРТ".

Задача 4.

Два стрелка выполняют по одному выстрелу в мишень. Вероятность удачного выстрела для первого стрелка составляет 0,8, для второго – 0,6. Найти вероятность того следующих событий:

а) в мишень попадет хотя бы один стрелок;

б) в мишень попадет только первый стрелок;

в) оба стрелка промахнутся.

Задача 5.

Игральную кость бросили 3 раза. Найти вероятность того, что три раза выпадет шесть очков.

Задача 6.

Монету бросают 5 раз. Найти вероятность того, что герб появится не менее 4 раз.

Задача 7.

Вероятность выигрыша команды в каждом матче равна 0,7. Сыграно 3 матча. Составить закон распределения количества выигрышей. Построить многоугольник распределения.

Задача 8.

Вычислить математическое ожидание и дисперсию, построить многоугольник распределения для дискретной случайной величины, заданной рядом распределения

Задача 9.

Дискретная случайная величина X задана законом распределения:

Найти интегральную функцию F(x) и построить ее график.

Задача 10.

Случайная величина X задана интегральной функцией:

.

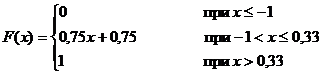Найти вероятность того, что в результате испытания величина X примет значение, заключенное в интервале .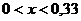

Задача 11.

Непрерывная случайная величина задана в интервале 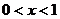дифференциальной функцией , а вне этого интервала . Найти ее числовые характеристики.

Задача 12.

Случайная величина Х имеет нормальное распределение с параметрами m = 30 и s = 5. Найти вероятность того, что в результате испытания случайная величина примет значение в интервале от 30 до 40.

Задача 12.

Задача 13.

Составить безынтервальный вариационный ряд, вычислить выборочное среднее, указать моду, медиану, по следующим данным:

16 18 18 20 22 22 23 25 25 25 28 30 30 32 33

Задача 14.

Составить интервальный вариационный ряд и построить гистограмму для следующих данных, разбив диапазон значений величины на три интервала

17 18 18 20 21 21 22 25 25 25 26 27 28 28 29 31 31 32 33 34 34

Задача 15.

Выборочная совокупность задана вариационным рядом. Найти объем выборки, указать относительные частоты, построить полигон и кумуляту.

Задача 16.

Найти выборочное среднее, дисперсию и среднее квадратическое отклонение, если выборка задана вариационным рядом:

Задача 17.

Измерены результаты в беге на 100 м: `x=14 с, sх=1,0 с, и в прыжке в длину с места: `y = 210 см, sу=20 см. Сравнить вариативность результатов при помощи коэффициента вариации.

Задача 18.

Определить статистическую ошибку выборочной средней, если в исследовании участвовало 25 человек, выборочная дисперсия s2=10.

Задача 19.

Выполнить округление выборочных средних, если результаты расчетов оказались следующими: `x=120,12596 mx = 2,2514 `у=12,15688, my = 0,12444.

Задача 20.

Составить доверительный интервал для генеральной средней с доверительной вероятностью 0,95, если по выборке объемом 16 получены следующие данные: `х=120, s=6.

Задача 21.

Оценить значение генеральной средней с доверительной вероятностью 0,95, если по выборке объемом n=100 получены следующие данные: `х=80, s = 5.

Задача 22.

Результаты тестирования в двух группах оказались следующими:`x=120, sx = 2, `у=128, sy = 4. Определить, различаются ли генеральные средние на уровне значимости 0,05, если численность групп составляет 5 и 8 человек, соответственно.

Задача 23.

В таблице указаны результаты тестирования двух групп юных спортсменов. Определить, достоверны ли различия в уровне развития физических качеств у участников исследования, если группа А состоит из 9 человек, группа В – из 10 человек.

Задача 24.

Проверить гипотезу о равенстве двух генеральных средних по связанным выборкам, если Х – результаты первичного тестирования, Y – результаты повторного тестирования

Задача 25.

Установить тесноту взаимосвязи между показателями Х и У при помощи коэффициента корреляции Браве-Пирсона.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6