Частное образовательное учреждение высшего профессионального образования

«Южно-Уральский институт управления и экономики»

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

по выполнению домашней контрольной работы

по дисциплине

«ТЕОРИЯ ВЕРОЯТНОСТЕЙ

И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА»

Для студентов заочной формы обучения

По направлению:

080100.62 «Экономика»

Челябинск

2012

Теория вероятностей и математическая статистика: Методические рекомендации по выполнению домашней контрольной работы / - Челябинск: ЧОУ ВПО «Южно-Уральский институт управления и экономики», 2012.- 30 с.

Теория вероятностей и математическая статистика: Методические рекомендации по выполнению домашней контрольной работы: 080100.62 «Экономика»

ã Издательство ЧОУ ВПО «Южно-Уральский институт управления и экономики», 2012

Частное образовательное учреждение высшего профессионального образования

«Южно-Уральский институт управления и экономики»

КОНТРОЛЬНАЯ РАБОТА

По дисциплине «Теория вероятностей и математическая статистика»

Вариант №___

Выполнил(а) студент(ка)

___________________________________________________________

(Фамилия, имя, отчество)

___________________________________________________________

(Адрес проживания)

Группа ______________________

Дата отправления «__» ____201_г.

Результат проверки____________________

Проверил преподаватель _______________

Дата проверки________________________

г. Челябинск, 2012

СОДЕРЖАНИЕ

Задачи изучения математики как фундаментальной дисциплины состоят в развитии логического и алгоритмического мышления, в выработке умения моделировать реальные процессы.

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ ЗАДАНИЙ

Теория вероятностей

Теория вероятностей - раздел математики, изучающий закономерности случайных явлений, наблюдаемых при массовых повторениях испытаний.

1. Случайные события

Основные понятия.

Под испытанием (опытом) понимается осуществление некоторого комплекса условий. Событием назовем всякий факт, который в результате опыта может произойти или не произойти.

Событие A в опыте называется достоверным, если при повторениях опыта оно всегда происходит.

Событие B в опыте называется невозможным, если при повторениях опыта оно никогда не происходит.

Событие в опыте называется случайным, если при повторениях опыта оно иногда происходит, иногда нет. Случайные события обозначаются А, В, С и т. д.

Два события называются несовместными (совместными), если появление одного из них исключает (не исключает) появление другого. Несколько событий в данном опыте называются несовместными, если они попарно несовместны. Несколько событий в опыте называются совместными, если совместны хотя бы

два из них.

События в опыте называются равновозможными, если условия их появления одинаковы и нет оснований считать какое-либо из них более возможным, чем любое другое.

Полной группой событий называется несколько событий таких, что в результате опыта непременно должно произойти хотя бы одно из них.

Пример 1 Опыт - бросание игральной кости; события :

А1 - выпадение одного очка,

А2 - выпадение двух очков,

А3 - выпадение трех очков,

А4 - выпадение четырех очков,

А5 - выпадение пяти очков,

А6 - выпадение шести очков,

В - выпадение четного числа очков,

С - выпадение более семи очков,

D - выпадение не менее трех очков,

E - выпадение не более шести.

Достоверное событие в данном опыте - E, невозможное событие - С, остальные события - случайные. Первые шесть событий А1, А2, А3, А4, А5, А6 не могут быть выражены через более простые события и их называют элементарными событиями (элементарными исходами). Кроме того, они образуют полную группу несовместных равновозможных событий. Событие В можно выразить через более простые события : либо наступит А2, либо наступит А4, либо А6; следовательно, элементарным событием событие В не является.

Два несовместных события, образующих полную группу, называются противоположными. Противоположные события обозначаются А и (не А).

Пример 2. Опыт - два выстрела по мишени; события: А - ни одного попадания, - хотя бы одно попадание.

2. Алгебра событий

Суммой или объединением событий А1, А2,..., Аn назовем событие, состоящее в появлении хотя бы одного из этих событий.

А1+А2+...+Аn=А1ÈА2È...ÈАn.

Произведением или пересечением событий А1, А2,..., Аn назовем событие, состоящее в совместном появлении всех этих событий.

А1· А2·…·Аn =A1∩A2∩...∩An.

Пример 3. Опыт - два выстрела по мишени. Событие Аi - попадание в мишень при i - м выстреле (i =1;2).

Тогда событие В=А1+А2 - хотя бы одно попадание, событие С= 1+2 – хотя бы один промах, событие D= А1·А2 - попадание в цель дважды, Е= А1·2 + 1·А2 - ровно одно попадание.

3. Частота события и ее свойства

Если опыт воспроизведен n раз, а событие А произошло m раз, то частотой (относительной частотой) события А назовем Р*(А)=, т. е. отношение числа испытаний, в которых появилось событие А, к числу всех испытаний.

Свойства частоты.

1) 0≤Р*(А)≤ 1, так как 0≤m≤n, следовательно, 0 ≤ ≤ 1

2) частота достоверного события равна 1, так как m=n.

3) частота невозможного события равна 0, так как m=0.

4) Р*(А+В)=Р*(А)+Р*(В)-Р*(А·В).

Условной частотой события В относительно события А, обозначение Р*(В/А), назовем частоту события В при условии, что событие А уже произошло, то есть это число равно отношению числа опытов NAB, в которых произошли события А и В одновременно, к числу опытов NA, в которых появилось событие А, то есть P*(B / A) =

5) Р*(А·В)=Р*(А)·Р*(В/А).

Частота случайного события обладает свойством устойчивости, т. е. при увеличении числа опытов значения частоты события группируются около некоторого числа, характеризующего возможность появления данного события в данном опыте.

4. Классическое определение вероятности события

Исход опыта называется благоприятным событию А, если в результате опыта событие А свершилось. Вероятностью события A назовем число Р(А)=, где m – число благоприятных событию А исходов, n – число всех исходов в данном опыте.

Пример 4. Опыт - бросание игрального кубика. Событие А - выпадение числа очков, кратного 3. Пусть X – число очков, тогда все возможные исходы нашего опыта: (Х=1), (Х=2), (Х=3), (Х=4), (Х=5), (Х=6), равновозможны. Всего случаев n=6, благоприятных из них m=2, следовательно,

P(A) = = .

5. Элементы комбинаторики

Имеется совокупность n объектов, назовем ее генеральной совокупностью. Из генеральной совокупности наудачу отбираем m объектов, эту отобранную совокупность назовем выборкой.

Выборка может быть упорядоченной, если порядок объектов (элементов) играет роль, и может быть неупорядоченной, если порядок элементов роли не играет.

Выборка может быть без повторений, если элементы повторяться не могут, и может быть с повторениями, если элементы в выборке повторяются.

Например, телефонный номер 260-61-51 - упорядоченная выборка с повторениями из десяти цифр по семи.

Упорядоченная выборка из n элементов по m называется размещением, неупорядоченная выборка из n элементов по m называется сочетанием. Число размещений и сочетаний c повторениями и без повторений из n элементов по m можно найти из следующей таблицы.

Таблица 1

Пример 5. Два счета из десяти выполнены с ошибками. Найти вероятность того, что из четырех взятых на проверку счетов один счет окажется с ошибками.

Решение.

Воспользуемся классической формулой Р(А)=, всего случаев , так как имеем дело с неупорядоченными выборками без повторений, благоприятных из них . Следовательно,

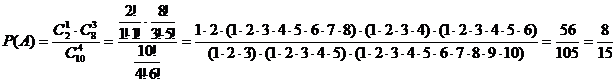
Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4