2. Сборщик получил 3 ящика деталей: в первом ящике 40 деталей, из них 20 окрашенных; во втором– 50, из них 10 окрашенных; в третьем – 30 деталей, из них 15 окрашенных. Найти вероятность того, что наудачу извлеченная деталь из наудачу взятого ящика окажется окрашенной.
3. На трех пресс-формах изготавливают детали, причем на первой вырабатывается 50% всех деталей; на второй 30% и на третьей – 20%. При этом вероятность появления брака с первой пресс-формы составляет 0,05; со второй – 0,08; с третьей – 0,1. Найти вероятность того, что наудачу взятая деталь, из числа изготовленных, соответствует стандарту.
4.Радиолампа поступает с одного из двух заводов с вероятностью 0,4 и 0,6 соответственно. Вероятность бесперебойной работы лампы составляет: для лампы первого завода – 0,1; второго завода – 0,2. Найти вероятность того, что лампа работает бесперебойно.
5. Фирма имеет три источника поставки комплектующих – фирмы А, В, С. На долю фирмы А приходится 50% общего объема поставок, В – 30% и С – 20%. Известно, что 10% поставляемых фирмой А деталей бракованные, фирмой В – 5% и фирмой С – 6%. Какова вероятность, что взятая наугад деталь будет бракованной?
6. Две литейные машины изготавливают по 250 однотипных отливок в смену, которые хранятся в одном месте. Для первой машины брак составляет 3%, а для второй – 2%. Найти вероятность того, что на удачу взятая отливка будет годной.
7. На сборку поступают детали из трёх заготовительных цехов. Известно, что первый цех даёт 3% брака, второй -2%, третий-1%. Найти вероятность попадания на сборку бракованной детали, если каждый цех поставляет, соответственно, 500, 200 и 300 деталей.
8. На складе хранятся 800 изделий завода №1 и 1200 изделий завода №2. Среди изделий завода №1 в среднем 95% высшего качества, а среди изделий завода №2 – 80%. Чему равна вероятность того, что первое принесённое со склада окажется низкого качества.
9. Трое рабочих за смену изготовили 60 деталей. Производительность рабочих относится как 1:2:3. Первый рабочий изготавливает в среднем 95% годных деталей, второй 85% и третий - 90%. Найти вероятность того, что наудачу взятая из числа изготовленных за смену деталь низкого качества.
10. Среди 100 деталей, изготовленных цехом №1, 85 деталей проходит закалку. Из числа 120 таких же деталей, изготовленных цехом №2, закалку проходят 95 деталей. Все эти детали поступают на сборку. Чему равна вероятность того, что наудачу взятая сборщиком деталь, прошла предварительную закалку?
ЗАДАНИЕ №3. Повторные независимые испытания. Формула Бернулли. Формула Пуассона. Формула Муавра-Лапласа.
1. Вероятность малому предприятию быть банкротом равна 0,2. Найти вероятность того, что из восьми малых предприятий сохранятся:
а) два,
б) более двух.
2. На факультете насчитывается 1825 студентов. Найти вероятность того, что 1 сентября является днем рождения четырех студентов.
3. В среднем 20% пакетов акций продаются на аукционе по первоначально заявленной цене. Найти вероятность того, что из 9 пакетов акций по первоначальной цене будет продано:
а) менее 2 пакетов,
б) хотя бы один пакет.
4. В поселке из каждых 100 семей 80 имеют холодильники. Найти вероятность того, что из 400 300 имеют холодильники.
5. Завод отправил на базу 10000 стандартных изделий. Среднее число поврежденных при транспортировке изделий составляет 0,02%. Найти вероятность того, что из 10000 изделий будет повреждено:
а) 3,
б) менее трех.
6. Предполагается, что 10%новых малых предприятий прекращают деятельность в течение года.
Найти вероятность того, что из 6 предприятий 2прекратят деятельность.
7. В среднем по 15% договоров страховая компания выплачивает страховую сумму. Найти вероятность того, что из 10 договоров с наступлением страхового случая страховая сумма будет выплачена по:
а) трем договорам,
б) менее двум договорам.
8.Контрольную работу по математике успешно выполняют 70 % студентов. Найти вероятность того, что из 400 студентов работу выполнят 180.
9.Учебник издан тиражом 10000 экземпляров. Вероятность того, что в учебнике есть опечатки равна 0,0001. Найти вероятность того, что тираж содержит:
а) 5 бракованных книг,
б) менее двух бракованных книг.
10. При проверке установлено, что пятая часть банков имеет уставной фонд свыше 100 млн. руб.
Найти вероятность того, что среди 1800 банков такой уставной фонд имеют:
а) не менее 300,
б)от 300 до 400.
ЗАДАНИЕ №4. Закон распределения вероятностей случайных дискретных величин. Числовые характеристики дискретных случайных величин. Функция распределения вероятностей случайной величины.
1. Вероятность попадания в цель при одном выстреле равна 0,8. Записать закон распределение Х – числа попаданий в цель при 4 выстрелах. Составить функцию распределения случайной величины F(x). Вычислить М(Х), Д(Х), sх.
2. По заданному закону распределения дискретной случайной величины Х:
Составить функцию распределения F(x) и изобразить ее график. Вычислить М(Х), Д(Х), sх.
3. Вероятность того, что в библиотеке необходимая студенту книга свободна, равна 0,3. Записать закон распределение Х – количества библиотек, которые посетит студент, если в городе 4 библиотеки. Составить функцию распределения случайной величины F(x). Вычислить М(Х), Д(Х), sх.
4. По заданному закону распределения дискретной случайной величины Х:
Составить функцию распределения F(x) и изобразить ее график. Вычислить М(Х), Д(Х), sх.
5. Студенту задается 3 вопроса. Вероятность ответа на каждый из них составляет 0,9. Записать закон распределение Х – числа ответов студента. Составить функцию распределения случайной величины F(x). Вычислить М(Х), Д(Х), sх.
6. По заданному закону распределения дискретной случайной величины Х:
Составить функцию распределения F(x) и изобразить ее график. Вычислить М(Х), Д(Х), sх.
7. Клиенты банка не возвращают кредиты с вероятностью 0,1. Составить закон распределения числа Х возвращенных кредитов из 4 выданных. Составить функцию распределения случайной величины F(x). Вычислить М(Х), Д(Х), sх.
8. По заданному закону распределения дискретной случайной величины Х:
Составить функцию распределения F(x) и изобразить ее график. Вычислить М(Х), Д(Х), sх.
9. Из урны, содержащей 3 белых и 4 черных шара, вынимают на удачу 3 шара. Найти закон распределения Х – числа вынутых черных шаров. Составить функцию распределения случайной величины F(x). Вычислить М(Х), Д(Х), sх.
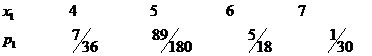 |
10. По заданному закону распределения дискретной случайной величины Х:
Составить функцию распределения F(x) и изобразить ее график. Вычислить М(Х), Д(Х), sх.
ЗАДАНИЕ №5 Статистическое распределение. Геометрическое изображение. Выборочные характеристики статистического распределения.
По данному статистическому распределению выборки вычислить:
а) выборочную среднюю,
б) выборочную дисперсию,
с) выборочное среднее квадратическое отклонение.
Построить полигон частот или гистограмму.
1.
xi | 110 | 115 | 120 | 125 | 130 | 135 | 140 |
ni | 3 | 7 | 11 | 40 | 19 | 12 | 8 |
2
xi | 120 | 130 | 140 | 150 | 160 | 170 | 180 |
ni | 6 | 9 | 29 | 26 | 14 | 11 | 5 |
3.
xi | 10,3 | 11,0 | 11,7 | 12,4 | 13,1 | 13,8 | 14,5 |
ni | 7 | 10 | 60 | 13 | 5 | 3 | 2 |
4
xi | 11,5 | 12,0 | 12,5 | 13,0 | 13,5 | 14,0 | 14,5 |
ni | 5 | 13 | 40 | 26 | 7 | 5 | 4 |
.
5.
xi | 42 | 50 | 58 | 66 | 74 | 82 | 90 |
ni | 4 | 17 | 55 | 12 | 7 | 3 | 2 |
6.
xi | 200-210 | 210-220 | 220-230 | 230-240 | 240-250 | 250-260 |
ni | 2 | 4 | 7 | 8 | 6 | 3 |
7.
xi | 190-200 | 200-210 | 210-220 | 220-230 | 230-240 | 240-250 |
ni | 5 | 2 | 4 | 8 | 6 | 5 |
8.
xi | 6-8 | 8-10 | 10-12 | 12-14 | 14-16 | 16-18 |
ni | 6 | 12 | 17 | 10 | 4 | 1 |
9.
xi | 0-3 | 3-6 | 6-9 | 9-12 | 12-15 | 15-18 |
ni | 1 | 1 | 5 | 9 | 14 | 20 |
10.
xi | 0-5 | 5-10 | 10-15 | 15-20 | 20-25 | 25-30 |
ni | 3 | 8 | 16 | 20 | 20 | 3 |
РЕКОМЕНДУЕМЫЙ СПИСОК ЛИТЕРАТУРЫ
Основная:
1. Вентцель, и упражнения по теории вероятностей: учеб. пособие для втузов / , . - 7-е изд., стер. - М.: Высш. шк., 2006. - 448 с.
2. Гмурман, к решению задач по теории вероятностей и математической статистике: учеб. пособие для вузов / . - 9-е изд., стер. - М.: Высш. шк., 2004. - 404 с.
3. Гмурман, к решению задач по теории вероятностей и математической статистике: учеб. пособие / . - 10-е изд., стер. - М.: Высш. шк., 2005. - 404 с.: ил.
4. Гмурман, к решению задач по теории вероятностей и математической статистике: учеб. пособие для вузов / . - 8-е изд., стер. - М.: Высш. шк., 2003. - 404 с.
5. Гмурман, вероятностей и математическая статистика: учеб. пособие / . - 11-е изд., стер. - М.: Высш. шк., 2005. - 479 с. : ил.
6. Коробейникова, вероятностей. Случайные величины: учеб. пособие / , . - Челябинск: АТОКСО, 2004. - 86с.
7. Кремер, вероятностей и математическая статистика: учеб. для вузов / . - 2-е изд., перераб. и доп. - М.: ЮНИТИ, 2006. - 573 с.
8. Кремер, вероятностей и математическая статистика: учебник для вузов / . - М.: ЮНИТИ, 2003. - 543 с.
9. Кремер, вероятностей и математическая статистика: учебник для студ. вузов / . - 3-е изд. - М.: ЮНИТИ, 2007. - 551 с.
Дополнительная:
1. Гнеденко, теории вероятностей: учеб. / . - 7-е изд., испр. - М.: Эдиториал УРСС, 2001. - 318 с.
2. Емельянов, по теории вероятностей и математической статистике : учеб. пособие / , . - 2-е изд., стер. - СПб.; М.; Краснодар: Лань, 2007. - 331 с.
3. Золотаревская, вероятностей. Задачи с решениями: учеб. пособие / . - 4-е изд., стереотип. - М.: УРСС, 2006. - 166 с.
4. Кожевников, вероятностей и математическая статистика: учеб. пособие для вузов / . - М.: Машиностроение, 2002. - 414 с. Коротков, вероятностей и математическая статистика: учебник / , , . – М.: ФОРУМ: ИНФРА-М, 2005.
5. Кочетков, вероятностей в задачах и упражнениях: учеб. пособие / , . - М.: Форум - Инфра-М, 2005. - 479 с.
6. Красс, математики и ее приложения в экономическом образовании. Учебник / , – М.: Дело, 2000
7. Розанов, вероятностей, случайные процессы и математическая статистика / . – М.: Наука, 2000.
8. Свешников, методы теории марковских процессов: учеб. пособие / . - СПб.; М.; Краснодар: Лань, 2007. - 189 с.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 |





