Запомните: 0!=1.
6. Основные теоремы
6.1 Теорема 1. Теорема сложения вероятностей.
Р(А1+А2+А3+...+Аn)=Р(А1)+Р(А2)+Р(А3)+...+Р(Аn) - Р(А1·А2) - Р(А1·А3) - … - Р(А1·Аn) - Р(А2·А3) - ... - P(An-1·An)+P(А1·А2·A3)+P(А1·А2·A4)+...+P(Аn-2·Аn-1·An)+...+ +(-1)n-1 P(A1·A2·...·An).
Следствие 1.
Если события А1, А2, ... ,Аn несовместны, то
Р(А1+А2+А3+...+Аn)=Р(А1)+Р(А2)+Р(А3)+...+Р(Аn).
Следствие 2.
Вероятность суммы двух любых событий равна сумме вероятностей этих событий без вероятности их произведения, то есть Р(А+В)=Р(А)+Р(В)–Р(А·В).
Замечание.
P(A) + P(![]() ) = 1, откуда P(
) = 1, откуда P(![]() ) = 1−P(A).
) = 1−P(A).
6.2 Теорема 2. Теорема умножения вероятностей.
Условной вероятностью Р(А/В) события А относительно события В назовем вероятность события А при условии, что событие В уже произошло.
Теорема умножения.
Р(А1·А2·А3·...·Аn)=Р(А1)·Р(А2/А1)·Р(А3/А1·А2) ·...·Р(Аn/А1·А2·А3·...·Аn-1).
Правило (теорема) умножения для двух событий. Вероятность произведения двух любых событий равна произведению вероятности одного из них на условную вероятность другого относительно первого, то есть
Р(А·В)=Р(А)·Р(В/А)=Р(В)·Р(А/В).
Событие А называется независимым от события В, если условная вероятность события А относительно события B равна безусловной вероятности события А, то есть Р(А/В)=Р(А). Нетрудно доказать, что если А не зависит от В, то и В не зависит от А.
Следствие. Если события А и В независимы, то Р(А·В)=Р(А)·Р(В).
Пример 6. Студент знает ответы на 20 из 25 вопросов. Какова вероятность того, что он ответит на два выбранных наудачу вопроса?
Решение.
Рассмотрим события: А- студент знает ответ на первый вопрос, В - студент знает ответ на второй вопрос. Найдем Р(А·В).
Р(А·В) = Р(А)·Р(В/А) = ![]()
Определение. Несколько событий называют независимыми (или независимыми в совокупности), если независимы каждые два из них и независимы каждое событие и все возможные произведения остальных.
Следовательно, если А1, А2, ... ,Аn независимы, то справедливо правило умножения для независимых событий
Р(А1·А2·А3·...·Аn)=P(A1)·P(A2)·P(A3)·...·P(An).
Пример 7. Два студента выполняют независимо друг от друга задание. Вероятность того, что задание будет выполнено первым студентом 0,6; для второго студента эта вероятность равна 0,8. Найти вероятность того, что
• оба студента выполнят задание;
• только один из них выполнит задание;
• хотя бы один из них выполнит задание.
Решение.
События: А - задание выполнит первый студент, В - задание выполнит второй студент. По условию Р(А) = 0,6; Р(В)=0,8; следовательно, Р(![]() ) = 1–0,6 = 0,4; P(
) = 1–0,6 = 0,4; P(![]() ) = 1–0,8 = 0,2.
) = 1–0,8 = 0,2.
• Р(А·В) = /события А и В - независимые события / = Р(А)·Р(В) = 0,6·0,8 = 0,48.
• Р(А·![]() +
+ ![]() ·B) = / A·
·B) = / A·![]() и
и ![]() ·B - несовместные события /= Р(А·
·B - несовместные события /= Р(А·![]() ) + Р(
) + Р(![]() ·B) = Р(А)·Р(
·B) = Р(А)·Р(![]() ) + Р(
) + Р(![]() )·Р(В) = 0,6·0,2 + 0,4·0,8 = 0,44.
)·Р(В) = 0,6·0,2 + 0,4·0,8 = 0,44.
• P(A+B)=/ А и В-совместные события /= Р(А)+Р(В)-Р(А·В)=0,6+0,8– –0,48=0,92.
6.3 Теорема 3. Формула полной вероятности
Пусть в результате опыта может появиться какое-либо из несовместных событий Н1, Н2,..., Нn, образующих полную группу. Событие А может появиться только вместе с одним из этих событий. События Н1, Н2,..., Нn называются гипотезами. Тогда вероятность события A равна P(A)=![]() P(Hi)P(A/Hi).
P(Hi)P(A/Hi).
Эта формула носит название формулы полной вероятности.
Пример 8. На стройку поступают блоки с трех баз, причем 50% с первой базы, 30% со второй базы, остальные с третьей базы. Вероятность того, что блок c первой базы бракованный - 0,09; со второй - 0,1; с третьей - 0,08. Найти вероятность того, что взятый наудачу на стройке блок окажется бракованным.
Решение.
Рассмотрим гипотезы:
Н1 -взятый наудачу блок поступил с первой базы,
Н2 -взятый наудачу блок поступил со второй базы,
Н3 -взятый наудачу блок поступил с третьей базы.
Тогда из условия Р(Н1)=50/100=0,5; Р(Н2)=30/100=0,3; Р(Н3)=(100-50-30)/100 = 0,2.
Событие А - взятый наудачу на стройке блок окажется бракованным.
По условию Р(А/Н1)=0,09; Р(А/Н2)=0,1; Р(А/Н3)=0,08.
Следовательно, по формуле полной вероятности
Р(А)=0,5·0,09+0,3·0,1+0,2·0,08=0,091.
6.4 Теорема 4. Формула Байеса (теорема гипотез)
Пусть в условиях предыдущей теоремы событие А наступило и мы нашли вероятность Р(А). Тогда вероятности гипотез в связи с появлением события А, т. е. найдем Р(Нi/А), равны ![]() где i=1,2,...,n.
где i=1,2,...,n.
Пример 9. В предыдущем примере событие А наступило, т. е. взятый наудачу на стройке блок оказался бракованным. Определить вероятность того, что этот блок поступил со второй базы.
Решение.
![]() .
.
6.5 Теорема 5. Формула Бернулли
Производится n независимых испытаний, в каждом из которых событие А наступает с постоянной вероятностью р. Вероятность того, что в этих n испытаниях событие А появится ровно m раз равно Pn(m)=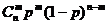 .
.
Пример 10. Каждый из пяти независимо работающих элементов отказывает с вероятностью 0,4. Найти вероятность того, что откажут три элемента из пяти.
Решение.
Р5(3)= ![]() =10·0,064·0,36 ≈ 0,23.
=10·0,064·0,36 ≈ 0,23.
7. Случайные величины
Случайной величиной Х в данном опыте называется переменная величина, которая в результате испытания примет одно из своих возможных значений, но какое именно до проведения опыта неизвестно.
Совокупность всех возможных значений случайной величины называется спектром. Спектр называется дискретным, если все возможные значения случайной величины образуют конечную или бесконечную последовательность, и называется непрерывным, если все значения случайной величины заполняют сплошь некоторый промежуток.
Например, Х - оценка на экзамене. Случайная величина Х имеет дискретный, т. к. ее возможные значения: 2; 3; 4; 5. Или Х - время безотказной работы двигателя. В этом случае случайная величина Х имеет непрерывный спектр, т. к. возможные значения Х заполняют сплошь некоторый промежуток времени [0;t], где t - момент отказа двигателя.
7.1 Функция распределения случайной величины
Функцией распределения F(x) случайной величины Х называется вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х, т. е. F(x)=P(X<x).
Из определения функции распределения следуют следующие свойства F(x):
1) область определения F(x) - интервал (- ∞;+∞),
2) 0 ≤ F(x) ≤1,
3) F(– ∞ )=0, так как P(X< – ∞ )=0,
4) F(+ ∞ )=1, так как P(X<+∞ )=1,
5) F(x) - неубывающая функция.
Законом распределения случайной величины Х называется любая ее вероятностная характеристика, из которой можно получить функцию распределения F(x).
Вероятность попадания случайной величины в промежуток и в точку
Если известна функция распределения F(x) случайной величины Х, то
P( α ≤ Х < β )=F(β)-F(α).
7.2 Дискретная случайная величина
Случайная величина Х называется дискретной, если ее спектр дискретный.
Законом распределения дискретной случайной величины Х является ряд распределения, т. е. перечисление всех возможных значений Х и их cоответствующих вероятностей:
рi=P(X=xi), где i=1;2;...;n;...
Многоугольником распределения назовем ломаную, соединяющую последовательно точки (х1;р1),(х2;р2),...,(хn;рn).
Пример 10. Среди шести элементов два изношенных. Составить ряд распределения случайной величины Х - числа изношенных элементов среди трех наудачу отобранных. Найти функцию распределения F(x) и построить ее график.
Решение.
Случайная величина Х может принимать значения: 0; 1; 2.
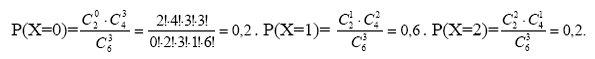
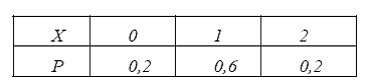
Условие нормировки: 0,2+0,6+0,2=1.
Найдем F(x).
Если x из (-∞;0], то F(x)=P(X<x)=0;
если x из (0;1], то F(x)=P(X<x)=P(X=0)=0,2;
если x из (1;2], то F(x)=P(X<x)=P(X=0)+P(X=1)=0,2+0,6=0,8;
если xиз (2;+ ∞ ), F(x)=P(X<x)=P(X=0)+P(X=1)+P(X=2)=0,2+0,6+0,2=1.
Следовательно,
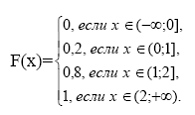
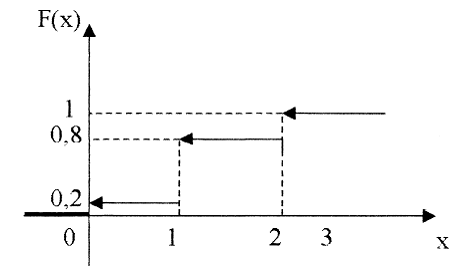
7.3 Непрерывная случайная величина

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 |





