Случайная величина Х называется непрерывной, если ее функция распределения F(x) непрерывна и имеет непрерывную производную везде, кроме, быть может, конечного числа точек. Из определения следует, что непрерывная случайная величина имеет непрерывный спектр (если случайная величина имеет непрерывный спектр, то из этого не следует, что она непрерывна). Если функция распределения F(x) на некоторых участках непрерывна, а в отдельных точках имеет разрывы, то случайная величина называется смешанной.

Плотностью распределения (или плотностью вероятности) непрерывной случайной величины X называется функция f(x) равная F’(x).

Отсюда следует, что

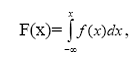
т. е. f(x) является законом распределения непрерывной случайной величины X.

Свойства f(x):

• f(x)≥ 0, т. к. F(x)- неубывающая функция,

•

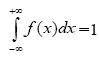
• Р(α≤X<β)=P(α≤X≤β)=Р(α<X≤β)=Р(α<x<β)=.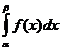

Пример 11. Плотность вероятности непрерывной случайной величины X

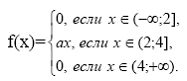
Найти

• значение параметра a ;

• функцию распределения F(x);

• вероятность того, что в четырех независимых испытаниях случайная величина X хотя бы один раз попадет в промежуток (0;3).

Решение.

• Из условия нормировки следует

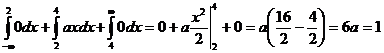, откуда . Итак

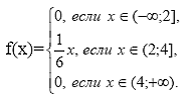
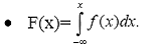
Если x из (-∞;2], то F(x)= =0;

если x из (2;4], то F(x)=;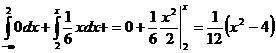

если xиз (4;+ ∞ ), F(x)= .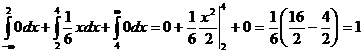

Следовательно,

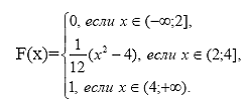
• Р(0<X<3)= F(3)-F(0)=

7.4 Основные числовые характеристики случайной величины

Закон распределения полностью характеризует случайную величину с вероятностной точки зрения. Однако при решении многих практических задач достаточно знать о случайной величине лишь характерные черты закона распределения, которые в сжатой форме выражают существенные особенности распределения.

О каждой случайной величине необходимо, прежде всего, знать ее среднее значение, около которого группируются возможные значения случайной величины, а также число, характеризующее степень разбросанности возможных значений относительно среднего значения случайной величины. Для более полного описания случайной величины используют и другие числовые характеристики.

Математическое ожидание случайной величины

Математическим ожиданием или средним значением дискретной случайной величины Х называется число

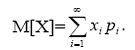
Если же дискретная случайная величина Х имеет n возможных значений, то

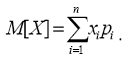
Таким образом, математическим ожиданием случайной величины называется сумма произведений всех возможных значений случайной величины на соответствующие вероятности этих значений.

Математическим ожиданием непрерывной случайной величины Х называется число

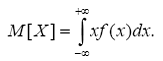
Если же возможные значения непрерывной случайной величины Х принадлежат лишь отрезку [ a ;b], то

Пример 12. Непрерывная случайная величина Х задана плотностью вероятности.

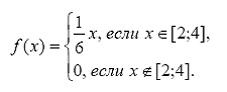
Найти М[X].

Решение.

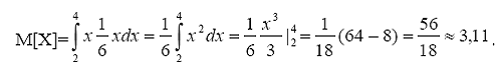
Простейшие свойства математического ожидания.

Свойство 1. Математическое ожидание постоянной величины равно самой постоянной, то есть М[C]=С.

Свойство 2. Постоянный множитель можно выносить за знак математического ожидания, то есть М[СX]=СM[X].

Дисперсия и среднее квадратическое отклонение случайной величины

Дисперсией случайной величины Х называется число, характеризующее степень разброса возможных значений случайной величины относительно ее математического ожидания, обозначаемое D[X] и равное D[X]=M[(X-M[X])2].

Следовательно, для дискретной случайной величины D[X] находят по формуле

mx – математическое ожидание M[X].

Для непрерывной случайной величины

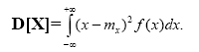
Средним квадратическим отклонением случайной величины Х называется число σx = , где Dx=D[X].

Среднее квадратическое отклонение σx также характеризует степень отклонения возможных значений случайной величины относительно ее mx, но имеет размерность случайной величины.

Простейшие свойства дисперсии.

Свойство 1. Дисперсия постоянной величины равна нулю. D[C]=0

Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его при этом в квадрат, т. е. D[СX]=С2D[X].

Свойство 3. Dx=M[X2]-mx2.

Пример 13. Найти дисперсию случайной величины Х, имеющей следующий закон распределения

Решение.

Воспользуемся формулой Dx=M[X2]-mx2.

Найдем М[X]=(-3)·0,2+(-1)·0,5+2·0,3=-0,5;

M[X2]= (-3)2·0,2+(-1)2·0,5+22·0,3=3,5; следовательно,

Dx=3,5-(-0,5)2=3,5-0,25=3,25. Можно вычислить σx = = ≈ 1,80.

Таблица соотношения начальной буквы фамилии студента и варианта контрольных заданий

Начальная буква фамилии

Вариант задания

А, Е, Л

Первый

Р, Х, Э

Второй

Б, Ж, М

Третий

С, Ц, Ю

Четвертый

В, З, Н

Пятый

Т, Ч

Шестой

Г, И, О

Седьмой

П, У, Ш

Восьмой

Д, Щ,

Девятый

Ф, К, Я

Десятый

ЗАДАНИЯ ДЛЯ ДОМАШНЕЙ КОНТРОЛЬНОЙ РАБОТЫ

ЗАДАНИЕ №1. Вероятность события. Теоремы сложения и умножения событий.

1. В лотерее 10 билетов, из которых 4 выигрышных. Какова вероятность выиграть хотя бы один раз, купив 3 билета?

2. У шести животных имеется заболевание, причем вероятность выздоровления равна 0,98. Какова вероятность того, что:

а) выздоровят все шестеро животных,

б) выздоровят четверо?

3. В магазине работают 2 мужчин и 7 женщин. Трое из них должны пойти в отпуск летом. Кто именно – определяется жребием. Найти вероятность того, что летом в отпуск пойдет хотя бы один мужчина.

4. Среди 10 документов, поступивших в офис, два оформлены с ошибками. Для проверки наудачу взяли 4 документа. Какова вероятность того, что среди ни окажется:

а) хотя бы один неверно оформленный документ,

б) только один неверно оформленный документ.

5. Рабочий обслуживает 3 станка, каждый из которых работает независимо друг от друга. Вероятность того, что станки потребуют ремонта равна соответственно: 0,4; 0,3; 0,2. Найти вероятность того, что придется ремонтировать все станки.

6. Среди 15 счетов 3 счета оформлены неверно. Ревизор наудачу берет 5 счетов. Найти вероятность того, что среди взятых счетов:

а) два оформлены неверно,

б) все оформлены верно.

7. В пачке 10 тетрадей, среди них 4 тетради в клетку, а остальные в линейку. Найти вероятность того, что среди наудачу взятых трех тетрадей хотя бы одна будет в клетку.

8. Из 20 методичек по математике 3 по теории вероятностей. Студент наудачу взял две методички.

Найти вероятность того, что среди взятых:

а) нет методичек по теории вероятностей,

б) есть одна методичка по теории вероятностей.

9.Из трех бухгалтеров, восьми менеджеров и шести научных работников необходимо сформировать комитет из 10 человек. Найти вероятность того, что в комитете окажутся: один бухгалтер, пять менеджеров и четыре научных работника.

10.В урне лежат 5 красных, 7 синих и 11 белых шаров. Какова вероятность, что вынутый шар окажется не белым?

ЗАДАНИЕ № 2. Теорема полной вероятности события.

1. Первый рабочий изготовил 40 деталей. Из которых 40 деталей, из которых 4 бракованных. Второй абочий изготовил 30 таких же деталей, из которых 2 бракованных. Все изготовленные детали положены в одну тару и доставлены в ОТК. Найти вероятность того, что деталь, взятая на удачу контролером ТК, соответствует ГОСТу.

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4