Исследование распределения магнитного поля в дисковом сепараторе с магнитной системой спирального типа (стр. 3 )

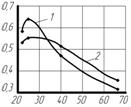
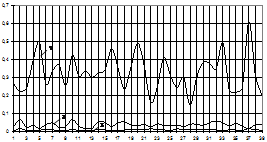
На следующем этапе численных исследований определялось влияние геометрических размеров постоянных магнитов на распределение магнитного поля. Результаты моделирования (рис. 6) представлены в виде зависимости максимального значения Вmax магнитной индукции от поперечного размера (ширины) а магнитов и воздушного зазора d (при Z=0).

а)

б)

в)

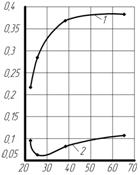
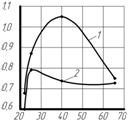
Рисунок 6 – Зависимости максимального значения магнитной индукции от геометрических размеров магнитной системы (1 – при d=25 мм;

2 –при d=50 мм) для характерных точек, расположенных: а) посередине полюса;

б) посередине воздушного зазора;

в) на границе магнит - воздушный зазор

Анализируя приведенные на рис. 6 зависимости, следует отметить, что с ростом ширины а магнитов (как при d= 25 мм, так и при d=50 мм) наблюдается снижение интенсивности поля для точек, лежащих посередине полюса и на границе магнит – воздушный зазор (рис. 6, а, в), при незначительном усилении поля в зоне воздушного зазора (рис. 6, б). Также необходимо отметить, что при d=50 мм магнитная индукция в области воздушного зазора (рис. 6, б) и в угловой зоне магнитов (рис. 6, в) существенно ниже, чем при меньшем значении величины воздушного зазора, равном d=25 мм. Аналогичная тенденция сохраняется и для магнитной индукции в области полюса магнита (рис. 6, а) при а= 20…33мм. Такой результат объясняется тем, что с увеличением величины воздушного зазора d уменьшаются размеры отдельных магнитов в направлении разворачивания спирали магнитной системы, что приводит к росту боковых потоков рассеяния и снижению числовых значений индукции. С учетом этих результатов, величину воздушного зазора d=25 мм следует считать наиболее приемлемой.

Зависимости, представленные на рис. 6, а, в, имеет явно выраженные точки экстремумов, на основании чего может быть сделан следующий вывод. Существуют некоторые оптимальные величины зазоров и размеров магнитов, соответствующие максимуму магнитной индукции. На этапе предварительных исследований (при низкой подвеске сепаратора над очищаемым материалом) может быть рекомендована ширина а постоянных магнитов из диапазона: а=25,5…39,7 мм.

Далее методом компьютерного моделирования выполнены предварительные исследования силового воздействия высокоградиентного неизменного во времени магнитного поля сепаратора на ферромагнитные частицы. Для этого была определена величина магнитной силы , действующей на извлекаемые ферромагнитные включения.

Магнитная сила , действующая на частицы, находящиеся во внешнем неоднородном магнитном поле, в общем виде описывается выражением [15]:

где – величина магнитного момента частицы;  – магнитная индукция внешнего неоднородного поля в месте расположения частицы.

Выражение (4) для силы , действующей на многодоменные ферромагнитные частицы в неоднородном магнитном поле, имеет вид [15]:

где – объем частицы; – магнитная восприимчивость материала частицы.

В выражении (5) можно выделить векторную функцию точки пространства r , численно равную магнитной силе, действующей на частицу единичного объема с единичной магнитной восприимчивостью, расположенную в этой точке [15]. Функция называется силовой функцией неоднородного магнитного поля и является его внутренней характеристикой.

Как следует из (5), для получения максимального значения силы необходимо стремиться не только к увеличению магнитной индукции , но и к повышению степени неоднородности магнитного поля в активной зоне магнита, т. е. стремиться к увеличению значения модуля вектора .

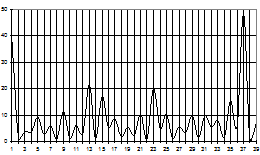
Распределение модуля силовой функции , определяющей согласно выражению (5) величину магнитной силы, действующей на частицы в рабочей зоне магнитной системы сепаратора, показано на рис. 7. Измерения силовой функции выполнялись в характерных точках в направлении разворачивания спирали магнитов: на поверхности магнитов (Z=0) – рис.7, а; на расстояниях Z=33 мм, 66 мм, 99 мм от поверхности магнитов – рис.7 б.

а)

б)

Рисунок 7 – Распределение векторной силовой функции в рабочей зоне магнитной системы: а) на поверхности магнитов (Z=0); б) на удалении от поверхности магнитов (1 – Z=33 мм; 2 – Z=66 мм; 3 – Z=99 мм)

Расчетные данные (рис. 7) свидетельствуют о том, что наибольшая сила локализована в угловых зонах магнитной системы на границе магнит - воздушный зазор. Кроме того, величина силы существенно снижается при удалении от поверхности магнитов.

Таким образом, для предложенной новой конструкции дискового магнитного сепаратора со спиральной магнитной системой на основе постоянных магнитов разработана компьютерная методика численного расчета распределения трехмерного магнитного поля и его силовой функции, позволяющая осуществлять предварительный выбор конструктивных параметров магнитной системы.

ВЫВОДЫ. Распределение магнитного поля в рабочей зоне существенно зависит от конфигурации магнитных систем. При этом наблюдается весьма большая разница между максимальным и минимальным значениями магнитной индукции на поверхности магнитов. По мере удаления от активной поверхности пульсации магнитной индукции значительно уменьшаются.

В результате анализа распределения магнитного поля в рабочей зоне установлено, что наиболее эффективной при низкой высоте подвески магнитного сепаратора над слоем сыпучего материала следует считать магнитную систему с максимальным числом полюсов. Однако с увеличением высоты подвески более предпочтительным оказывается использование магнитной системы с меньшим числом полюсов.

Оценка влияния геометрических размеров постоянных магнитов на распределение магнитного поля показала, что на этапе предварительных исследований при низкой подвеске сепаратора над очищаемым материалом расчетную ширину постоянных магнитов рекомендуется выбирать из диапазона а=25,5…39,7 мм, а величину воздушного зазора принимать равной d=25 мм.

Результаты предварительных исследований силового воздействия высокоградиентного неизменного во времени магнитного поля сепаратора на ферромагнитные частицы свидетельствуют о том, что наибольшая сила локализована в угловых зонах магнитной системы на границе магнит - воздушный зазор, а величина силы существенно снижается при удалении от поверхности магнитов.

Результаты проведенных исследований могут быть использованы для выбора оптимальных параметров магнитной системы сепаратора, т. к. существуют некоторые оптимальные величины зазоров и размеров магнитов, соответствующие максимуму магнитной индукции.

Окончательное суждение о реальной картине поля, а также о результатах проведенных расчетов можно будет сделать по итогам экспериментального исследования опытного образца, находящегося в процессе изготовления.

ЛИТЕРАТУРА

1. Земзюлин траектории направленного выбора новой конструкции дискового магнитного сепаратора / , // Вісник Східноукраїнського національного університету імені Володимира Даля. – 2012. - №– Частина 2. – С.58-63.

2. Пат. 21724 Україна, МПК В 03 С 1/24. Дисковий магнітний сепаратор «ДМС» / І., , Шатірішвілі О. В, Шатірішвілі В. О.; заявник та власник І., , Шатірішвілі О. В, Шатірішвілі В. О. – № u 2007 00182; заявл. 09.01.07; опубл. 15.03.07, Бюл. № 3.

3. Загирняк сепараторы. Проблемы проектирования: [монография] / М. В. Загирняк, , ; под ред. М. В. Загирняка. – К.: Техніка, 2011. – 224 с.

4. А. с. 94773 СССР, МКИ3 В 03 С 01/16. Дисковый магнитный сепаратор / (СССР). – № 000/9113; заявл. 18.09.50.

5. А. с. 1639756 СССР МКИ3 В03 С 1/18. Железоотделитель / , А. П. Нестеренко, , В. Н. Капустянов (CCCР). – № 000/03; заявл. 22.12.88; опубл.07.04.91, Бюл. №13.

6. Пат. 61551 Україна, МПК В 03 С 1/24. Дисковий магнітний сепаратор / Шведчикова І. О., Земзюлін М. О., ; заявник і власник Східноукраїнський національний університет імені Володимира Даля. – №u 2010 14974; заявл. 13.12.10; опубл. 25.07.11, Бюл. № 14.

7. COMSOL Multiphysics, version 3.5а. AC/DC Module Reference Guide. – .

8. Ansys EmagTM [Электронный ресурс]: Electromagnetic simulation are critical to electrical and electronic product designs across many industries. – Режим доступа: http://www. /products/emag. asp.

9. ELCUT® [Электронный ресурс]: Программа моделирования электромагнитных, тепловых и механических задач. – Режим доступа: http://*****/.

10. Finite Element Method Magnetics [Электронный ресурс]: – A Windows finite element solver for low frequency 2D and axisymmetric magnetic problem. – Режим доступа: http://femm. .

11. Милых трехмерного распределения магнитного поля мощного турбогенератора в режиме холостого хода / Милых В. И., // Електротехніка і електромеханіка. – 2011. – № 3. – С. 30-32.

12. Matagne E., Cividyan G., Kluyskens V. Exact Expression of Corner Reluctances in a Magnetic Circuit of Rectangular Section // Computer Field Models of Electromagnetic Devices. – 2010. – P. 136-143.

13. Пятин магниты / . – М.: Энергия, 1980. – 487 с.

14. Антонов машины магнитоэлектрического типа / . – К.: НАН Украины, Институт электродинамики, 2011. – 216 с.

15. Кириленко силового воздействия высокоградиентного магнитного поля на магнитные наночастицы в потоке жидкости / , , [и др.] // Доповіді Національної Академії наук України. – 2010. – № 9. – С. 162-172.

THE RESEARCH OF MAGNETIC FIELD DISTRIBUTION IN THE DISK SEPARATOR WITH MAGNETIC SYSTEM OF SPIRAL TYPE

I. A. Shvedchikova, M. A. Zemzulin

East-Ukrainian Volodymyr Dal National University,

kv. Molodezhniy, 20a, Lugansk, 91034, Ukraine, E-mail: *****@***ua

New design of disk magnetic separator for clearing of granular materials with magnetic system of spiral type is proposed. It is grounded that the placing of permanent magnets in a spiral way increases the efficiency of discharging of extracted ferromagnetic impurities. It is done the numerical calculation of the three-dimensional magnetic field and magnetic force in the working zone with taking into account the real separator design. It is found that the distribution of the magnetic field in the air gap significantly depends on the configuration of magnetic systems. It is shown that the magnetic system with a maximum number of poles should be regarded as the most effective in the case of low suspension of separator over the layer of granular material. There are presented the results of preliminary calculations of the field for different geometric relations of the active part and the mass of the permanent magnets. The results of research can be used for choosing of optimal parameters of separator magnetic system.

Кey words: magnetic separator, permanent magnet, magnetic field, finite element method.

REFERENCES

1. Zemziulin, M. A. and Shvedchikova, I. A. (2012), “Rationale of trajectory of directed selection of new structure disc type magnetic separator”, Visnyk Skhidnoukrajinskogo natsionalnogo universytetu imeni Volodimira Dahlya, Vol. 14, pp. 58-63/

2. Pat. 21724 Ukrajina, MPK B 03 C 1/24. Diskoviy magnitniy separator “DMS” / Baralyuk V. І., Moskalenko S., Shatіrіshvіlі O. V., V. O. Shatіrіshvіlі; zayavnik ta vlasnik Baralyuk V. І., Moskalenko S., Shatіrіshvіlі O. V., Shatіrіshvіlі V. O. - № u 2, zajavl. 09.01.07, opubl. 15.03.07, Bjul. № 3

3. Zagirnjak, M. V., Branspiz, Yu. A. and Shvedchikova, I. A. Magnitnie separatory. Problemy proektirovanija [Magnetic separators. Problems of designing], Tekhnika, Kiev, Ukraine.

4. A. s. 94773 SSSR, MKI3 B 03 C 01/16. Diskoviy magnitniy separator / A. Ya. Sochnev (SSSR). – №434699/9113; zajavl. 18.09.50.

5. A. s. 1639756 SSSR, MKI3 B 03 C 1/18. Zhelezootdelitel / V. O.Kartashyan, A. P. Nesterenko, I. A. Shvedchikova, V. N. Kapustyanov (SSSR). – № 000/03; zayavl. 22.12.88; opubl.07.04.91, Bjul. №13.

6. Pat. 61551 , MPK B 03 C 1/24. Diskoviy magnitniy separator / Shvedchikova I. A., Zemziulin M. A., Khokhola T. V.; zayavnik ta vlasnik Skhidnoukrajinskiy natsionalniy universitet imeni Volodymira Dahlja. – №u 2010 14974; zajavl. 13.12.10; opubl. 25.07.11, Bjul. № 14.

7. COMSOL Multiphysics, version 3.5а. AC/DC Module Reference Guide. – .

8. Ansys EmagTM “Electromagnetic simulation are critical to electrical and electronic product designs across many industries”, available at: http://www. /products/emag. asp.

9. ELCUT® “Program of modeling electromagnetic, thermal and mechanical tasks”, available at: http://*****/.

10. Finite Element Method Magnetics, “A Windows finite element solver for low frequency 2D and axisymmetric magnetic problem” available at: http://femm. .

11. Milykh, V. I. and Vysochin, A. I. (2011), “Calculation of 3D distribution of the magnetic field of a powerful turbo generator in an idling mode”, Elektrotekhnika I electromekhanika, Vol. 3, pp. 30-32.

12. Matagne E., Cividyan G., Kluyskens V., (2010), “Exact Expression of Corner Reluctances in a Magnetic Circuit of Rectangular Section”, Computer Field Models of Electromagnetic Devices, pp. 136-143.

13. Pjatin, Yu. M. (1980), Postojannie magnity [Permanent magnets], Energija, Moscow, Russia.

14. Antonov, A. E. (2011), Elektricheskije mashiny magnitoelektricheskogo tipa [Electrical machines of magnetoelectrical type], NAN Ukrainy, Institut elektrodinamiky, Kiev, Ukraine.

15. Kirilenko, A. V., Chekhun, V. F., Podoltsev, A. D. and others (2010), “Analysis of the force action of a high-gradient magnetic field on magnetic nanoparticles in a flowing fluid”, Dopovidi Natsionalnoji Akademiji nauk Ukrainy, Vol. 9, pp. 162-172.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3