Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
Уфимский государственный авиационный технический университет
Кафедра автоматизированных систем управления
Курсовая работа по дисциплине
«Имитационное моделирование экономических процессов»
Вариант 5
Выполнил:
Студ. ФИРТ
Гр. ПИЭ-413
Проверил:
Уфа 2008г.
Содержание
1. Введение. 3
2. Постановка задачи. 6
3. Блок схема алгоритма имитационной модели. 7
4. Общий вид и описание программы.. 8
5. Листинг программного кода. 10
5.1 SMO. mat 10
5.2 Dimon. mat 13
5.3 dimonstat. mat 14
6. Заключение. 16
7. Список используемой литературы.. 17
1. Введение
Имитационное моделирование — это метод, позволяющий строить модели, описывающие процессы так, как они проходили бы в действительности. Такую модель можно «проиграть» во времени как для одного испытания, так и заданного их множества. При этом результаты будут определяться случайным характером процессов. По этим данным можно получить достаточно устойчивую статистику.
Имитационное моделирование — это метод исследования, при котором изучаемая система заменяется моделью с достаточной точностью описывающей реальную систему и с ней проводятся эксперименты с целью получения информации об этой системе. Экспериментирование с моделью называют имитацией (имитация — это постижение сути явления, не прибегая к экспериментам на реальном объекте).
Имитационное моделирование — это частный случай математического моделирования. Существует класс объектов, для которых по различным причинам не разработаны аналитические модели, либо не разработаны методы решения полученной модели. В этом случае математическая модель заменяется имитатором или имитационной моделью.
Имитационная модель — логико-математическое описание объекта, которое может быть использовано для экспериментирования на компьютере в целях проектирования, анализа и оценки функционирования объекта.
К имитационному моделированию прибегают, когда:
Ø дорого или невозможно экспериментировать на реальном объекте;
Ø невозможно построить аналитическую модель: в системе есть время, причинные связи, последствие, нелинейности, стохастические (случайные) переменные;
Ø необходимо сымитировать поведение системы во времени.
Цель имитационного моделирования состоит в воспроизведении поведения исследуемой системы на основе результатов анализа наиболее существенных взаимосвязей между ее элементами или другими словами – разработке симулятора (английский термин – simulation modeling) исследуемой предметной области для проведения различных экспериментов. Имитационную модель можно рассматривать как множество правил (дифференциальных уравнений, карт состояний, автоматов, сетей и т. п.), которые определяют, в какое состояние система перейдёт в будущем из заданного текущего состояния. Имитация – это процесс «выполнения» модели, проводящий её через (дискретные или непрерывные) изменения состояния во времени.
Имитационное моделирование позволяет имитировать поведение системы, во времени. При чём плюсом является то, что временем в модели можно управлять: замедлять в случае с быстропротекающими процессами и ускорять для моделирования систем с медленной изменчивостью. Можно имитировать поведение тех объектов реальные эксперименты с которыми, дороги, невозможны или опасны.
Имитация, как метод решения нетривиальных задач, получила начальное развитие в связи с созданием ЭВМ в 1950х — 1960х годах.
Можно выделить две разновидности имитации:
Ø Метод Монте-Карло (метод статистических испытаний);
Ø Метод имитационного моделирования (статистическое моделирование).
Виды имитационного моделирования:
Ø Агентное моделирование – относительно новое (1990е-2000е гг.) направление в имитационном моделировании, которое используется для исследования децентрализованных систем, динамика функционирования которых определяется не глобальными правилами и законами (как в других парадигмах моделирования), а наоборот. Когда эти глобальные правила и законы являются результатом индивидуальной активности членов группы. Цель агентных моделей – получить представление об этих глобальных правилах, общем поведении системы, исходя из предположений об индивидуальном, частном поведении ее отдельных активных объектов и взаимодействии этих объектов в системе. Агент – некая сущность, обладающая активностью, автономным поведением, может принимать решения в соответствии с некоторым набором правил, взаимодействовать с окружением, а также самостоятельно изменяться.
Ø Дискретно-событийное моделирование – подход к моделированию предлагающий абстрагироваться от непрерывной природы событий и рассматривать только основные события моделируемой системы такие как: «ожидание», «обработка заказа», «движение с грузом», «разгрузка» и другие. Дискретно-событийное моделирование наиболее развито и имеет огромную сферу приложений – от логистики и систем массового обслуживания до транспортных и производственных систем. Этот вид моделирования наиболее подходит для моделирования производственных процессов. Основан Джеффри Гордоном в 1960х годах.
Ø Системная динамика – парадигма моделирования, где для исследуемой системы строятся графические диаграммы причинных связей и глобальных влияний одних параметров на другие во времени, а затем созданная на основе этих диаграмм модель имитируется на компьютере. По сути, такой вид моделирования более всех других парадигм помогает понять суть происходящего выявления причинно-следственных связей между объектами и явлениями. С помощью системной динамики строят модели бизнес-процессов, развития города, модели производства, динамики популяции, экологии и развития эпидемии. Метод основан Форрестером в 1950 годах.
Области применения:
Ø Бизнес процессы
Ø Боевые действия
Ø Динамика населения
Ø ИТ-инфраструктура
Ø Математическое моделирование исторических процессов
Ø Логистика
Ø Пешеходная динамика
Ø Производство
Ø Рынок и конкуренция
Ø Сервисные центры
Ø Цепочки поставок
Ø Уличное движение
Ø Управление проектами
Ø Экономика здравоохранения
Ø Экосистемы
2. Постановка задачи
Производственный объект находится под воздействием пуассоновского потока отказов с интенсивностью λ. Отказавший объект немедленно начинает ремонтироваться (полностью восстанавливаться). Распределение времени восстановления экспоненциальное с интенсивностью µ.
Требуется определить;
– коэффициент использования (готовности) объекта;
– среднее время восстановления объекта
Разумные значения λ и µ и единицы измерения времени выбрать самостоятельно.
3. Блок схема алгоритма имитационной модели
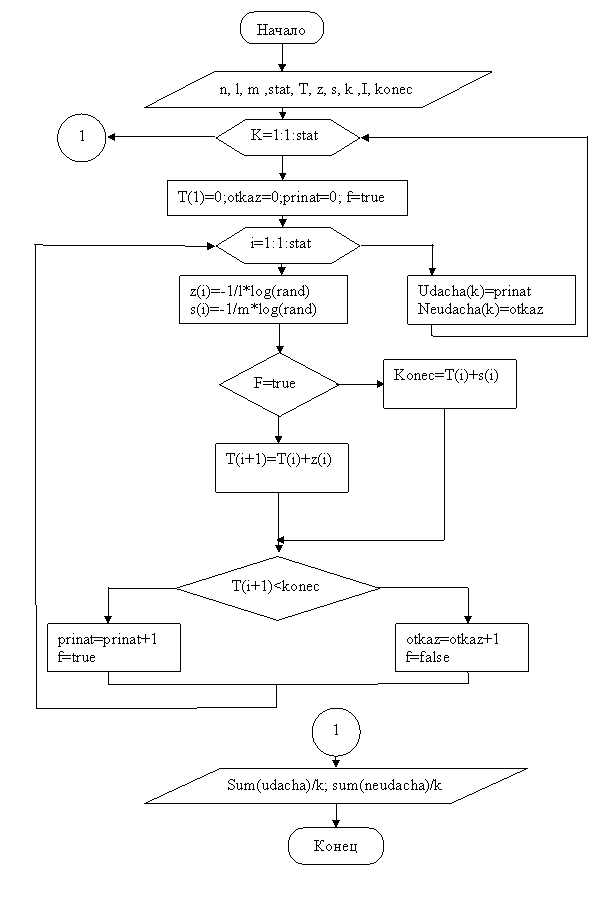

4. Общий вид и описание программы
Общий вид программы представлен ниже. (рис. 1)
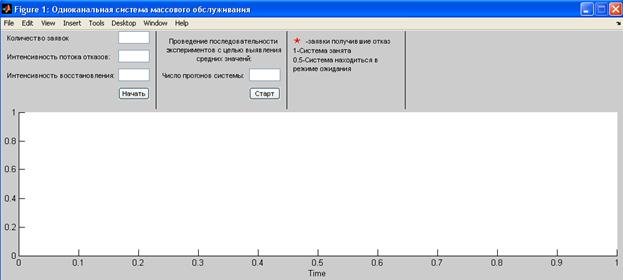
Рисунок 1 Общий вид программы
Данная программа написана на М-языке системы MATLAB.
Для запуска программы необходимо в командном окне системы MATLAB ввести имя М-файла : smo. В результате должно появиться окно, представленное на рисунке 1. Для запуска имитационной модели необходимо заполнить 3 левых поля и нажать на кнопку начать, как это показано на рисунке 2.
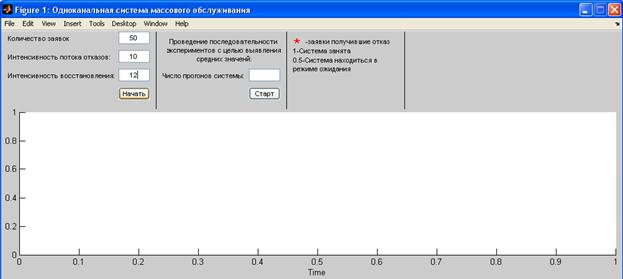
Рисунок 2 Запуск имитационной модели
В результате вы должны получить график-ход работы модели (рис.3). Данная графическая иллюстрация включает в себя следующие обозначения:
Ø 0.5 - система находиться в режиме ожидания;
Ø 1 – система находиться в режиме обслуживания;
Ø * - заявка, получившая отказ;
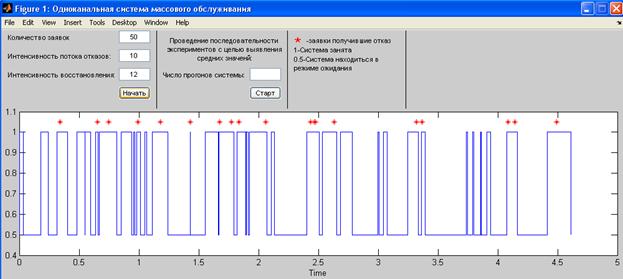
Рисунок 3 Графическая иллюстрация работы модели
Для того что бы получить статистический анализ данных, необходимо ввести количество прогонов системы и нажать на кнопку “Старт”. В результате мы получим график со значениями количества обслуженных заявок при каждом запуске системы, а также необходимые результаты (рис. 4).

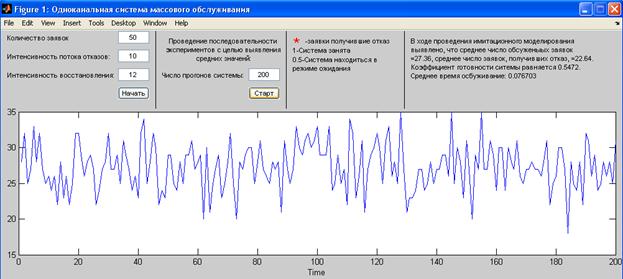
Рисунок 4 Статистический анализ работы модели
Если количество прогонов системы в ходе статистического анализа велико, необходимо дождаться окончания процесса - появиться окно ожидания (рис. 5).
Рисунок 5 Окно ожидания окончания работы системы
5. Листинг программного кода
Программа состоит из 3х M-файлов:
Ø Smo. m –отвечает за внешний вид программы;
Ø Dimon. m – построение имитационной модели и отображения графика ее работы;
Ø Dimonstat. m – сбор статистической информации и построение графика.
Ниже приведены листинги данных M - файлов.
5.1 SMO. mat
function smo
% Описание глобальных переменных--
global hFig hAxes
global hEditn hEditl hEditm hEditstat
global hButStart hButStat
global hTxt1 hTxt2 hTxt3 hTxt4 hTxt5 hTxt6
%
hFig=figure('Position',[],'Resize','off',...
'name','Одноканальная система массового обслуживания',...
'Interruptible','off');
hAxes=axes('Parent',hFig,'Color',[1 1 1],...
'Units','pixels','Position',[30],...
'FontSize',10);
xlabel('Time');
% Описание компонентов для ввода данных
hEditn=uicontrol (hFig,'Style','edit',...
'BackgroundColor',[1 1 1],...
'Position',[]);
hEditl=uicontrol (hFig,'Style','edit',...
'BackgroundColor',[1 1 1],...
'Position',[]);
hEditm=uicontrol (hFig,'Style','edit',...
'BackgroundColor',[1 1 1],...
'Position',[]);
hEditstat=uicontrol (hFig,'Style','edit',...
'BackgroundColor',[1 1 1],...
'Position',[]);
% Описание компонентов для отображения текстовой информации
hTxt1=uicontrol (hFig,'Style','Text',...
'BackgroundColor',[],...
'Position',[10 ],...
'HorizontalAlignment','left',...
'String','Количество заявок');
hTxt2=uicontrol (hFig,'Style','Text',...
'BackgroundColor',[],...
'Position',[10 ],...
'HorizontalAlignment','left',...
'String','Интенсивность потока отказов: ');
hTxt3=uicontrol (hFig,'Style','Text',...
'BackgroundColor',[],...
'Position',[10 ],...
'HorizontalAlignment','left',...
'String','Интенсивность восстановления:');
hTxt4=uicontrol (hFig,'Style','Text',...
'BackgroundColor',[0 0 0],...
'Position',[]);
hTxt5=uicontrol (hFig,'Style','Text',...
'BackgroundColor',[],...
'Position',[],...
'HorizontalAlignment','Center',...
'String','Проведение последовательности экспериментов с целью выявления средних значенй:');
hTxt6=uicontrol (hFig,'Style','Text',...
'BackgroundColor',[],...
'Position',[],...
'HorizontalAlignment','left',...
'String','-заявки получившие отказ');
hTxt7=uicontrol (hFig,'Style','Text',...
'BackgroundColor',[0 0 0],...
'Position',[]);
hTxt8=uicontrol (hFig,'Style','Text',...
'BackgroundColor',[],...
'Position',[],...
'HorizontalAlignment','left',...
'FontSize',20,'ForegroundColor',[1 0 0],...
'String','*');
hTxt9=uicontrol (hFig,'Style','Text',...
'BackgroundColor',[],...
'Position',[],...
'HorizontalAlignment','left',...
'String','1-Система занята');
hTxt10=uicontrol (hFig,'Style','Text',...
'BackgroundColor',[],...
'Position',[],...
'HorizontalAlignment','left',...
'String','0.5-Система находиться в режиме ожидания');
hTxt11=uicontrol (hFig,'Style','Text',...
'BackgroundColor',[],...
'Position',[],...
'HorizontalAlignment','left',...
'String','Число прогонов системы:');
hTxt7=uicontrol (hFig,'Style','Text',...
'BackgroundColor',[0 0 0],...
'Position',[]);
% Описание компонентов-кнопок
hButStart=uicontrol (hFig,'Style','pushbutton',...
'Position',[],...
'String','Начать',...
'Callback','dimon');
hButStart=uicontrol (hFig,'Style','pushbutton',...
'Position',[],...
'String','Старт',...
'Callback','dimonstat');
5.2 Dimon. mat
function dimon;
global hAxes hEditn hEditl hEditm n
global hTxt1 hTxt2 hTxt3 hTxt4
%Получаем информацию с полей ввода данных
strn=get(hEditn,'String');
strl=get(hEditl,'String');
strm=get(hEditm,'String');
%Конвертируем строковые переменные в числовые-------
n=str2num(strn);
l=str2num(strl);
m=str2num(strm);
% Имитационная модель одноканальной СМО--
T(1)=0;
otkaz=0;
prinat=0;
axes(hAxes);
cla;
xlabel('Time');
plot([0,0],[0.4,0.4]);
f=true;
for i=1:1:n
hold on;
z(i)=-1/l*log(rand);
s(i)=-1/m*log(rand);
if f
konec=T(i)+s(i);
line([T(i),T(i)],[0.5,1]);
line([T(i),konec],[1,1]);
line([konec, konec],[1,0.5]);
end
T(i+1)=T(i)+z(i);
if (T(i+1)<konec)
otkaz=otkaz+1;
plot(T(i+1),1.05,'r*');
f=false;
else
prinat=prinat+1;
line([konec, T(i+1)],[0.5,0.5]);
f=true;
end; end;
5.3 dimonstat. mat
function dimonstat;
global hFig hAxes hEditn hEditl hEditm hEditstat
global hTxt1 hTxt2 hTxt3 hTxt4 htxt12
%Получаем информацию с полей ввода данных
strn=get(hEditn,'String');
strl=get(hEditl,'String');
strm=get(hEditm,'String');
strstat=get(hEditstat,'String');
%Конвертируем строковые переменные в числовые-------
n=str2num(strn);
l=str2num(strl);
m=str2num(strm);
stat=str2num(strstat);
% Имитационная модель одноканальной СМО--
h=waitbar(0,'Please, wait until data proccesing...');
for k=1:1:stat
waitbar(k/stat, h);
T(1)=0;
otkaz=0;
prinat=0;
f=true;
for i=1:1:n
hold on;
z(i)=-1/l*log(rand);
s(i)=-1/m*log(rand);
if f
konec=T(i)+s(i);
end
T(i+1)=T(i)+z(i);
if (T(i+1)<konec)
otkaz=otkaz+1;
f=false;
else
prinat=prinat+1;
f=true;
end;
end;
udacha(k)=prinat;
neudacha(k)=otkaz;
end;
close(h);
axes(hAxes);
cla;
hTxt12=uicontrol (hFig,'Style','Text',...
'BackgroundColor',[],...
'Position',[],...
'HorizontalAlignment','left',...
'String',['В ходе проведения имитационного моделирования выявлено, что среднее число обсуженыых заявок =' num2str(sum(udacha)/k)...
', среднее число заявок, получивших отказ, =' num2str(sum(neudacha)/k)...
'. Коэффициент готовности ситемы равняется ' num2str(sum(udacha)/(sum(udacha)+sum(neudacha)))...
'. Среднее время осбуживание: ' num2str(sum(s)/n)]);
try
plot(udacha);
catch
errordlg('Пожалуйста, укажите число прогонов системы','ErrorMessage');
end
end
6. Заключение
Если не можете добиться результата,
имитируйте кипучую деятельность
и бешеную активность.
(Из законов Мэрфи: следствие Эндрю)
Имитационные моделирование на сегодняшний день является мощным средством для анализа в случае, когда невозможно, либо слишком дорого проведение опытов на реальном объекте. Также имитационное моделирование показывает свое преимущество над аналитическим решением задачи, в случае, когда присутствует фактор времени, сложные причинные связи, случайные переменные.
Имитационное моделирование позволяет имитировать поведение системы, во времени. При чём плюсом является то, что временем в модели можно управлять: замедлять в случае с быстропротекающими процессами и ускорять для моделирования систем с медленной изменчивостью.
Таким образом имитация является востребованным методом моделирования в различных областях деятельности.
7. Список используемой литературы
1. , “Имитационное моделирование. Классика CS.” 3-е изд. - СПб.: Питер
2. Мартынов. Н. Н. “Введение в MATLAB 6.x” –Кудиц-Образ: Москва 2002
3. http://matlab. *****/




