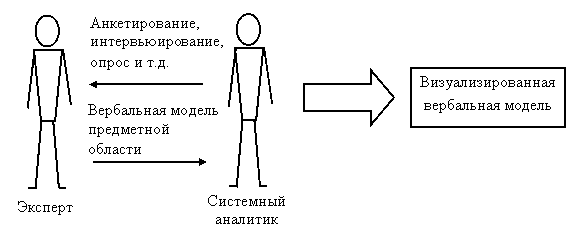
Рис.40. Схема моделирования существующего бизнес-процесса

Важнейшая цель вербализации – погружение специалиста по системному моделированию в предметную область и специфику конкретного бизнес-процесса, учитывающую особенности управляющей системы, корпоративную культуру и традиции. Параллельно вербализации необходимо выяснить организационную структуру, связанную с бизнес-процессом и попытаться изобразить её графически. В результате вербализации специалист должен в целом представлять бизнес-процесс, логику его функционирования и структуру управления им.

После вербализации осуществляется визуализация полученных о бизнес-процессе знаний в виде графических схем, диаграмм и алгоритмов или аналитических выражений, т. е. формирование графической модели системы.

5.6.1. Методология SADT. Для проектирования информационных систем существуют различные методологии, среди которых можно выделить методологию SADT – методологию системного анализа и проектирования, принятую в США.

Методология SADT включает ряд стандартов для структурно-семантического моделирования сложных систем, наиболее популярными из которых являются:

-  IDef0 – функциональное моделирование;

-  IDef1X – моделирование данных;

-  IDef3 – моделирование «потока» процессов;

-  IDef4 – объектно-ориентированное проектирование и анализ;

-  IDef5 – определение онтологий и др. (см. [30]).

5.6.2. Функциональное моделирование. Для формирования системной модели (рис.41) в SADT можно использовать любой из перечисленных стандартов, но наиболее подходящим являются стандарт IDef0, поскольку он позволяет наиболее полно раскрывать структуру процессов организованной системы.

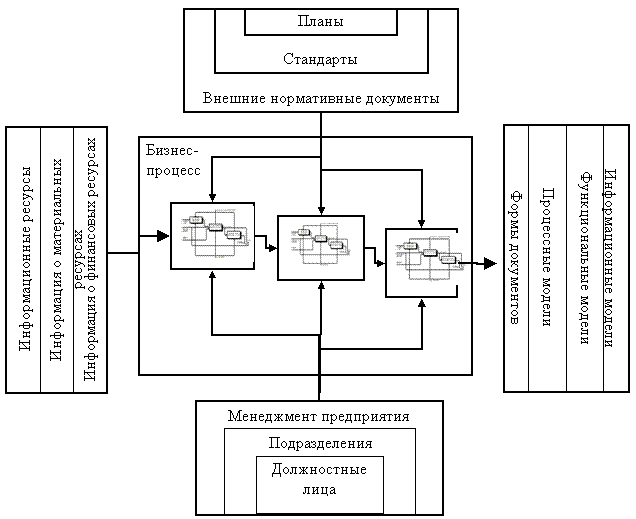
Рис.41. Построение системной модели бизнес-процесса

Функциональная модель (ФМ) описывается формулой:

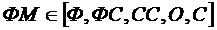, (4.1)

где Ф – функции; ФС – функциональные связи; СС – статистические свойства; О – отношения; С – семантика.

Функциональная IDef0-модель представляет собой ориентированный граф (G) вида:

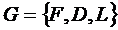, (4.2)

где F = {F1, F2, …} – множество вершин; D = {CB1, CB2, …} – множество ориентированных дуг; – отношение инцидентности.

Представление функционального блока IDef0 показано на рис.42.

Рис.42. Графическое представление процесса в IDef0

Суть моделирования организованных систем в IDef0 заключается в представлении их в виде перечня действий по преобразованию ресурсов.

При этом Входы моделируют преобразуемые в процессе объекты (ресурсы), а Выходы – результаты этого преобразования.

Например, если на входе функции «Согласования учебного плана» был объект «Проект учебного плана», то на выходе будет объект «Согласованный учебный план».

Поэтому Входы и Выходы называют преобразуемыми ресурсами, а Управления и Механизмы – непреобразуемыми ресурсами. Управления – это ресурсы, устанавливающие порядок и правила выполнения процесса. К ним относят: методы, стандарты, решения. Данный тип ресурсов не изменяем в ходе реализации процесса, поэтому они называются не устаревающими или не изменяющими состояний. Механизмы, напротив, могут изменять своё состояние при выполнении процесса, поскольку они включают производительные силы и средства труда: персонал, оборудование, инструмент, оснастку и т. д. Поэтому механизмы называют устаревающими или изменяющими состояния ресурсами (рис.43).

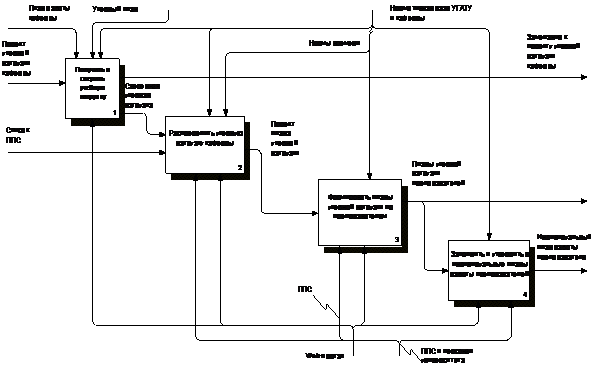
Рис.43. Пример функциональной модели управления учебными ресурсами

Если при создании функциональной модели, возникает проблема отсутствия или неполноты информации, требуемой для визуализации её структуры, то возможен переход на предшествующий этап системного анализа и дополнительные исследования системы с помощью известных или оригинальных методов.

Более подробно о стандарте IDef0 можно узнать в [17].

5.6.3. Объектно-ориентированное моделирование. Объектно-ориентированное моделирование опирается на объектный подход. Объектный подход предполагает построение моделей, связанных с понятием объекта (класса), который служит для связи данных и функции по их обработке, что позволяет конструировать структуру обобщающих понятий над объектной структурной моделью (рис.44). Важнейшим понятием объектной технологии является объект, определяемый как определённая сущность, обладающая свойствами и методами. Объекты – это основные элементы, моделирующие реальный мир. В отличие от структурного подхода, где основное внимание уделяется функциональной декомпозиции, в объектном подходе предметная область разбивается на множество достаточно независимых сущностей – объектов [34].

Экземпляр объекта – это определенный элемент множества.

Например, в лесу объект – это некий клён, а экземпляр этого объекта – конкретный клён, растущий возле поворота дороги.

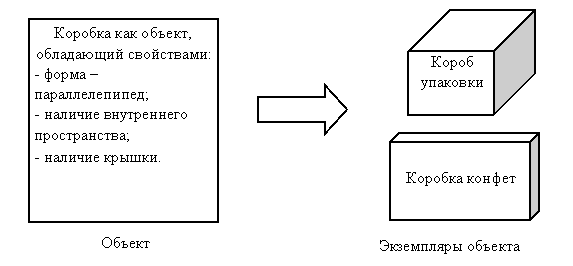
Рис.44. Связь между объектом и экземплярами объекта

Класс – это набор элементов реального мира, связанных структурой и функциями (поведением). Элемент класса – это конкретный элемент данного набора. При этом объект включается в класс и является его представителем, а термины «экземпляр объекта» и «элемент класса» равнозначны.

Метод – реализация операции над данными (функции) для объектов класса.

Свойство объекта – это количественная характеристика объекта.

Ресурсы, с точки зрения рассматриваемого подхода, должны быть скрыты. Сокрытие данных и методов для объекта получило название инкапсуляции. Инкапсуляция придаёт объекту целостность, очерчивая его границы и функции.

Полиморфизм – способность объекта принадлежать одновременно к нескольким типам.

Объектная модель активно использует аппарат наследования, что позволяет справляться с колоссальным количеством и разнообразием управляемых компонентов и их атрибутов. Наследование означает построение новых классов на основе существующих с возможностью добавления или переопределения данных и методов (рис.45).

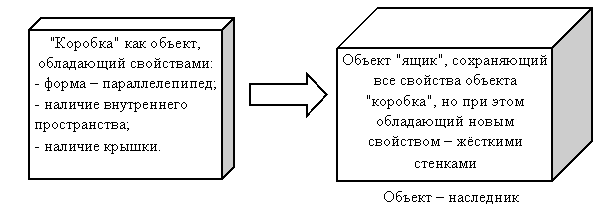
Рис.45. Свойство наследования объектов

Класс объектов, кроме структур данных, определяет функции (методы), применимые к этим структурам. Класс – это элемент, обеспечивающий модульность в проектных спецификациях информационных систем и программных решениях.

Например, основная образовательная программа – это класс, в который как объекты входят отдельные дисциплины.

Объектно-ориентированная система строится с учетом её эволюции. Ключевые элементы объектного подхода: наследование и полиморфизм обеспечивают возможность определения новой функциональности классов объектов с помощью создания производных классов – потомков базовых классов. Потомки наследуют характеристики родительских классов без изменения их первоначального описания и добавляют при необходимости собственные структуры данных и методы. Определение производных классов, при котором задаются только различия или уточнения, позволяет экономить время при производстве и использовании спецификаций и программного кода.

Объектно-ориентированный анализ наилучшим образом подходит для проектирования информационных систем, основанных на ситуационном подходе к управлению сложными объектами. Объектно-ориентированное моделирование облегчает процесс взаимопонимания между разработчиком, экспертом и заказчиком системы.

5.6.4. Информационное моделирование. Методология IDEF1X – это и формализованный язык для семантического моделирования данных, и инструмент для анализа информационных структур систем различной природы.

Информационное моделирование представляет собой анализ логической структуры информации об объектах системы, дополняя функциональные модели, путём детализации объектов, которыми манипулируют функции системы. Информационная модель демонстрирует взаимосвязь между данными и документами, выявляя разделяемые атрибуты в них (рис.46).

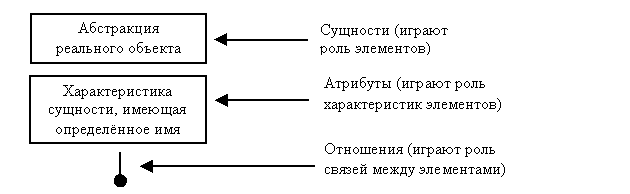
Рис.46. Определение понятий «сущность», «атрибут» и «отношение» [17]

Например, для учебного процесса можно выделить сущности «основная образовательная программа» и «дисциплина», связанные отношением «один-ко-многим». Атрибутами этих сущностей могут быть «название направления подготовки», «трудоёмкость изучения» и т. д.

Информационная модель (ИМ) в нотации «сущность-связь» может быть выражена следующей формулой:

, (4.3)

где СУЩ = {СУЩ1, СУЩ2, …} – сущности; СВ – связи; АТ – атрибуты.

Теоретической базой построения информационных моделей является теория баз данных типа «сущность-связь».

Следует отметить, что информационная модель, соответствующая IDef1X, может быть сформирована из функциональной модели, построенной с учётом требований стандарта IDef0. При этом стрелки функциональной модели всех видов становятся потенциальными сущностями, а функции, связывающие их, трансформируются в отношения между ними.

Построенная по указанным выше правилам информационная модель будет являться адекватным отображением информационной структуры сущностей и их отношений.

При реализации информационной модели может возникнуть необходимость приведения её к какой-либо нормализованной форме.

5.6.5. Моделирование семантики. Семантической моделью называют систему значений или область объектов, которые превращают формулы логического исчисления в истинные или ложные утверждения.

Семантическая сеть – один из способов представления знаний. В семантической сети роль вершин выполняют понятия базы знаний, а дуги (причем направленные) задают отношения между ними (рис.47). Таким образом, семантическая сеть отражает семантику предметной области в виде понятий и отношений [9].

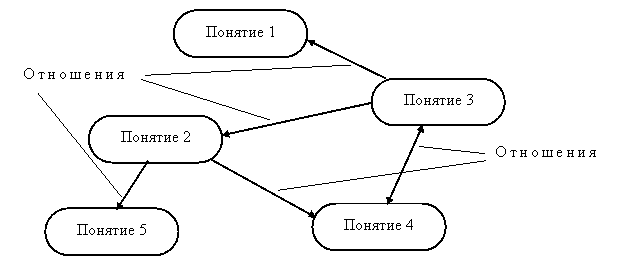
Рис.47. Пример семантической сети

Наиболее ярким и популярным примером семантических сетей являются Сети Петри, представленные разновидностью ориентированных двудольных графов. Двудольный граф включает вершины двух типов: позиции (обозначаются кружками) и переходы (обозначаются планками).

Сеть Петри может быть формально представлена как совокупность множеств [7]:

N = (P, T, G, W), (4.4)

где P = {p1, p2… pn} – множество всех позиций (n – количество позиций); Т = {t1, t2… tm} – множество переходов (m – количество переходов); G = (Gp-t, Gt-p) – множество дуг сети: Gp-t = (p´t), Gt-p = (t´p) – множества дуг, ведущих соответственно от переходов к позициям и от позиций к переходам (дуг, соединяющих однородные вершины, не существует); W = {w1, w2… wk} – множество весов дуг (k – количество дуг).

Каждая позиция может быть маркирована, т. е. содержать некоторое число фишек. Если обозначить числа фишек, находящихся в i-й позиции pi, как mi, то маркировка всей сети: M = {m1, m2… mn}.

Тогда полное определение сети Петри, включая данные о начальной маркировке, можно записать в виде:

PN = (N, M0), (4.5)

где М0 – начальная маркировка сети.

При моделировании процессов принятия решений с помощью сетей Петри её позиции интерпретируют собой условия, состояния, значения переменных и т. д. Переходы интерпретируют собой принятие логических решений, соответствующих выполнению действий, при этом входные позиции – условия выполнения действий, выходные позиции – результат выполнения действий.

Если осуществить начальную маркировку сети Петри, то можно описать логику работы системы и произвести анализ ее работоспособности. Переходы меток описываются графом достижимости, у которого каждой вершине соответствует определенная маркировка, а каждой дуге – переход, который срабатывает при данной маркировке (рис.48).

Таким образом, граф достижимости представляется как:

GD = (V, E), (4.6)

где V – массив вершин (маркировок, соответствующих вершинам):

V = {М1, М2 … Мq}, (4.7)

где Мi – i-я маркировка, q – количество маркировок; Е = {e1, e2 … ep} – массив дуг, связывающих вершины (р – количество дуг).

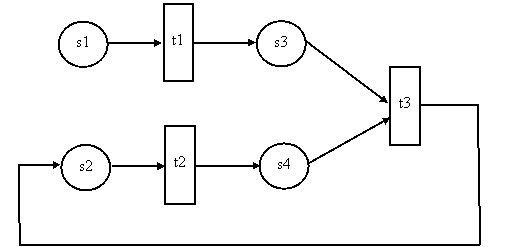
Рис.48. Пример графа сети Петри

Каждая дуга представляется как совокупность ei = {a1, a2, Т}, где a1 и a2 – номера начальной и конечной вершин графа; Т = {t1, t2, … tk} – массив переходов, соответствующий дуге; k – количество одновременно срабатывающих переходов при переходе от одной маркировки к другой.

С помощью графа достижимости могут быть определены следующие свойства сети Петри:

-  живость (отсутствие тупиковых состояний);

-  ограниченность (сеть ограниченна, если символ «w» не входит ни в одну вершину графа);

-  безопасность (сеть безопасна, если в метки вершин входят только «0» и «1») – физически безопасность означает отсутствие зацикливаний;

-  правильность (если сеть безопасная и живая, то она правильная);

-  обратимость (сеть обратима, если в графе имеется хотя бы одна дуга, направленная к начальной маркировке М0);

-  пассивность переходов (переход ti пассивен, если он не соответствует ни одной дуге графа);

-  число возможных состояний Nсост.

5.7. Контрольные вопросы

1)  Что такое зафиксированная в пространстве, наблюдаемая, физически реализуемая совокупность звеньев структуры системы?

2)  Каково соотношение понятий «изоморфизм», «гомоморфизм» и «полиморфизм»?

3)  Что такое модель системы?

4)  Что такое моделирование?

5)  Каковы принципы моделирования?

6)  Какой принцип утверждает, что модель стро­ится для решения только определенного вида задач?

7)  Какие виды моделирования Вы знаете?

8)  Каковы принципы имитационного моделирования?

9)  Как связаны понятия «вербализация» и «визуализация» при моделировании бизнес-процессов?

10)  Что общего и различного в функциональном, объектно-ориентированном и информационном моделировании?

11)  Каким образом связаны понятия «сущность» и «атрибут» в информационной модели?

12)  Что представляет собой граф достижимости в сети Петри?

6. Измерение в системном анализе

6.1. Понятие шкалы

6.1.1. Роль измерений в системном анализе. Современное общество ориентировано на высокие технологии, которые опираются на высокую точность исполнения отдельных операций. Например, для изготовления современной микроэлектроники необходимо наносить линии толщиной в несколько микрон. Такая точность в технике повышает требования к точности и в других сферах. Поэтому при решении исследовательских задач необходимо задумываться о мере точности ожидаемых результатов. Решение этой задачи в точных науках связано с понятием погрешности измерений. Погрешность измерения – оценка отклонения измеренного значения величины от её истинного значения [9]. Для измерения же с той или иной погрешностью используется шкала. Шкала – сопоставление результатов измерения какой-либо величины и точек числовой прямой [9].

В настоящее время шкалы активно используются и в управленческих науках. С помощью шкал можно ранжировать различные элементы сложных систем.

6.1.2. Шкалы и их атрибуты. С точки зрения метрологии в основе измерения лежит сопоставление значений качественных или количественных характеристик исследуемой системы значениям соответствующих шкал (обычно метрических).

Формально шкалой называется кортеж из трех элементов , где X реальный объект, Y шкала, гомоморфное отображение X на Y [4].

При этом:

X = {x1, x2 … xn, Rx} измеряемая система, включающая множество свойств xi, на которых в соответствии с целями измерения задано некоторое отношение Rx. В процессе измерения необходимо каждому свойству xi Î X поставить в соответствие признак или число, его характеризующее;

Y = {j (x1), j (x2), … j (xn), Ry} знаковая система с отношением, являющаяся отображением измеряемой системы в виде некоторой образной или числовой системы, соответствующей измеряемой системе;

j Î Ф – гомоморфное отображение X на Y, устанавливающее соответствие между X и Y так, что {j (x1), j (x2), … j (xn)} Î Ry только если (x1, x2 … xn) Î Rx.

Тип шкалы определяется по Ф = {j1, j2, … jm}, множеству допустимых преобразований xi ® yi.

В соответствии с приведенными определениями, охватывающими как количественные, так и качественные шкалы, измерение системы X с отношением Rx состоит в определении знаковой системы Y с отношением Ry, соответствующей ей. Предпочтения Rx на множестве X´X в результате измерения переводятся в знаковые соотношения Ry на множестве Y´Y.

Шкалы разделяются по типу, в соответствии с тем, какие отношения они отражают. Каждой шкале соответствуют допустимые для данной шкалы математические преобразования. Выделяют три основных атрибута измерительных шкал, наличие или отсутствие которых определяет принадлежность шкалы к той или иной категории:

1)  Упорядоченность данных показывает, что один пункт шкалы, соответствующий выраженности измеряемого свойства, больше, меньше или равен другому пункту (рис.49).

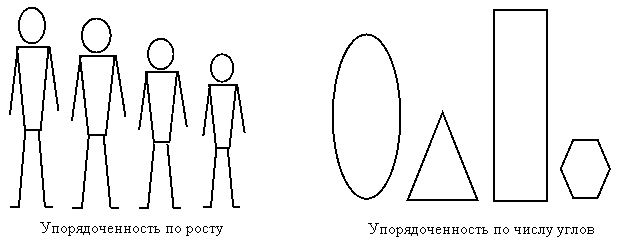
Рис.49. Примеры упорядоченности шкал

Например, школьников в классе можно упорядочить по росту или алфавиту.

2)  Интервальность пунктов шкалы означает, что интервал между любой парой чисел, соответствующих выраженности измеряемого свойства, больше, меньше или равен интервалу между другой парой чисел. Например, расстояния между городами можно измерить и, соответственно, можно найти 2 пары городов, находящихся на одном расстоянии (интервалы равны) или на разных расстояниях (интервалы не равны) (рис.50).

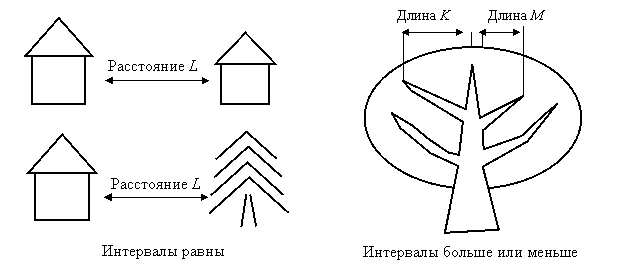
Рис.50. Примеры интервальности шкал

3)  Нулевая точка (или точка отсчета) означает, что набор чисел, соответствующих выраженности измеряемого признака, имеет точку отсчета, обозначаемую за 0, что соответствует полному отсутствию измеряемого и свойства (рис.51). Например, про некоторый сосуд можно сказать, что он пуст, т. е. количество воды в нём – 0, а про времена года нельзя сказать, что наступило их отсутствие.

Рис.51. Примеры шкал с нулевой точкой и без неё

Под измерительной шкалой подразумевается некоторый ряд элементов, с которым можно соотносить для измерения значения свойств реальной системы.

6.2. Виды измерительных шкал

Типы шкал имеют иерархическую упорядоченность по сложности. Рассмотрим виды измерительных шкал:

1)  В номинативной шкале нет всех основных атрибутов измерительных шкал: упорядоченности, интервальности, нулевой точки (рис.52). Эту шкалу могут называть «шкалой наименований» или «номинальной шкалой». Номинативная шкала используется для идентификации объектов (группировки по классам, каждому из которых приписывается число), причём объекты группируются по классам таким образом, чтобы внутри класса они соответствовали друг другу по измеряемому свойству. Это самая простая шкала из тех, что могут рассматриваться как измерительные, хотя, по сути, эта шкала не связана с понятием «величина», а значит мало подходит для измерения. Её задача – различение объектов в рамках некоторой выборки.

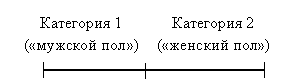
Рис.52. Пример номинативной шкалы

Для исключения неопределенности в классификации объектов, следует выбирать взаимоисключающе категории, измеряемые в номинативной шкале. Более того, они должны быть исчерпывающими, что выражается в том, что любому значению должна однозначно соответствовать заданная категория. Категории данных в номинативной шкале должны включать сопоставимые экземпляры.

Категории измеряемой переменной не являются численными и над ними невозможны арифметические операции, но их можно сравнивать друг с другом на основе статистики наблюдений, относящихся к ним.

С помощью номинативной шкалы можно распределить по категориям, например, дисциплины в учебном плане.

В порядковой шкале из всех основных атрибутов шкал присутствует только упорядоченность. Такие шкалы называют «ранговыми шкалам».

Результатом использования такой шкалы является упорядочение объектов. Шкала ранжирует объекты, приписывая им числа в зависимости от выраженности измеряемого свойства по некоторому признаку (в порядке убывания или возрастания). В отличие от номинативной шкалы, здесь можно не просто определить, что один объект отличен от другого, но и что по определенному признаку один объект больше или меньше другого. Порядковая шкала показывает, больше или меньше выражено свойство (измеряемая величина), но не насколько больше, или насколько меньше оно выражено, а тем более – во сколько раз больше или меньше. Порядковая шкала популярна в социальных и гуманитарных исследованиях. Примером измерения в порядковой шкале является социально-экономический статус, определяемый в категориях: 1) «богатые», 2) «зажиточные», 3) «бедные». Эти категории ранжируются, например, по признаку уровня дохода (рис.53).

Рис.53. Пример порядковой шкалы

Возможности арифметических действий в порядковых шкалах ограничены. Использование большинства операций с порядковыми данными математически некорректно. В то же время, шкала может вполне корректно использоваться в некоторых экспериментальных исследованиях.

Порядковая шкала может помочь составить список задач кафедры, упорядочив их по важности.

2)  В интервальной шкале присутствуют два основных атрибута – упорядоченность и интервальность. Для обозначения такой шкалы используется термин «шкала интервалов». В интервальной шкале исследуемому объекту присваивается число единиц измерения, пропорциональное выраженности измеряемого свойства. Соответствующие интервалы разных участков шкалы имеют одно и то же значение. Поэтому измерения в интервальной шкале допускают не только классификацию и ранжирование, но и точное определение различий между категориями (рис.54).

Рис.54. Пример интервальной шкалы

Типичным примером интервальной шкалы являются температурные шкалы Цельсия и Фаренгейта. Например, если сегодня уличный термометр фиксирует температуру -10оС, а вчера было -20оС, мы можем сказать, что сегодня теплее на 10 градусов. В интервальных шкалах (например, шкалах Цельсия и Фаренгейта нет нулевой точки отсчета). Точнее, выбор нулевой точки в интервальной шкале условен (произволен). Имея данные, представленные в интервальной шкале, можно судить, насколько больше или насколько меньше выражено измеряемое свойство, но не о том, во сколько раз больше или меньше. Для таких шкал характерна произвольность выбора нулевой точки, а значит значение «0» не соответствует полному отсутствию измеряемого свойства. Измерения не соответствуют абсолютному количеству измеряемого свойства. Для интервальных шкал можно корректно использовать большинство математических операций. Однако на практике часто возникают сложности при интерпретации показателей, определяемых как отношение измерений, полученных в интервальных шкалах.

Интервальная шкала может использоваться для оценки уровня компетенций преподавателей, поскольку он не может быть как нулевым, так и абсолютным.

3)  В относительной шкале присутствуют все атрибуты измерительных шкал: упорядоченность, интервальность, нулевая точка (рис.55). Эту шкалу можно называть «шкалой подобия». Относительная шкала позволяет оценивать, во сколько раз свойство одного объекта больше (меньше) аналогичного свойства другого объекта, принимаемого за эталон, единицу. Эта шкала характеризуется всеми атрибутами интервальной шкалы и имеет фиксированную нулевую точку (0), которая не является условной, она соответствует полному отсутствию измеряемого свойства.

Рис.55. Пример относительной шкалы

Например, переменная «количество сотрудников» имеет фактическое начало отсчета, т. к. нулевое значение соответствует отсутствию сотрудников вообще. Аналогично, нулевое значение может соответствовать отсутствию образования, дохода, детей, количеству лет в браке и т. п.

В силу фиксированности нулевой точки, можно судить при сравнении исследуемых объектов не только о том, насколько больше или меньше выражено свойство, но и во сколько раз больше или меньше оно выражено. Для относительной шкалы возможно корректное использование всех математических процедур обработки данных. Такие шкалы часто применяют для оценки объективных параметров объекта (температура, размеры, уровень напряжения).

Абсолютная шкала может быть использована для измерения многих характеристик учебного процесса, например, таких как число студентов, число часов, отведённых на практические занятия и т. д.

4)  Шкалы разностей применяются в тех случаях, когда необходимо измерить, насколько один объект превосходит по определенному свойству другой объект. В шкалах разностей неизменными остаются разности численных оценок свойств (рис.56).

Рис.56. Пример шкалы разностей

Примерами измерений в шкалах разностей могут служить измерения прироста продукции предприятий (в абсолютных единицах) в текущем году по сравнению с прошлым, увеличение численности учреждений, количество приобретенной техники за год, летоисчисление и т. д.

Как и шкалы отношений, шкалы разностей являются частным случаем шкал интервалов, получаемых выбором единицы масштаба измерений. Точка отсчета в шкалах разностей может быть произвольной.

Шкалы разностей, как и шкалы интервалов, сохраняют отношения интервалов между оценками пар объектов, но, в отличие от шкалы отношений, не сохраняют отношения оценок свойств объектов.

Разностная шкала в предметной области, связанной с учебным процессом, может применяться в отчёте кафедры для демонстрации изменения числа статей, контингента студентов и т. д. за равные периоды (семестры, учебные года).

5)  Абсолютными называют шкалы, в которых единственными допустимыми преобразованиями φ являются тождественные преобразования:

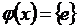, (5.1)

где e(x) = x.

Это означает, что существует только одно отображение эмпирических объектов в числовую систему. Отсюда и название шкалы, так как для неё единственность измерения понимается в буквальном абсолютном смысле.

Абсолютные шкалы являются частным случаем ранее рассмотренных типов шкал, поэтому сохраняют любые соотношения между оценками измеряемых свойств объектов: различие, порядок, отношение интервалов, отношение и разность значений и т. д.

Кроме указанных типов шкал, существуют промежуточные типы, такие как степенная шкала и её разновидность – логарифмическая шкала.

При проведении измерений нужно отделять существенно несравнимые альтернативы от несравнимых альтернатив, допускающих косвенную сравнительную оценку (рис.57).

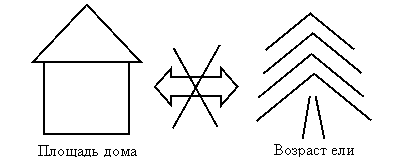
Рис.57. Пример несравнимых характеристик

Особенностью измерения и оценивания качества сложных систем является то, что для одной системы по разным частным показателям качества могут применяться любые из типов шкал от самых слабых до самых сильных. При этом для получения надежного значения показателя может проводиться несколько измерений. Кроме того, обобщенный показатель системы может представлять собой некую осредненную величину однородных частных показателей. При измерении и оценке физических величин обычно трудностей не возникает, так как перечисленные величины измеряются в абсолютной шкале. Более сложной является оценка в качественных шкалах. Однако отдельные показатели в процессе системного анализа уточняются, и, как следствие, появляется возможность от измерения и оценки в качественных шкалах перейти к оценке в количественных шкалах. Более подробно классификация и характеристики шкал рассмотрены в [4].

6.3. Квалиметрия в системном анализе

С развитием систем менеджмента качества и появлением международного стандарта ISO 9001 (в Российской Федерации – ГОСТ Р ИСО 9001 [9)]), особенно начиная с третьей версии, вышедшей в 2000 году, большую роль стало играть измерение качественных характеристик. Например, в учебном процессе часто необходимо оценить степень усвоения знаний студентами или измерить качество научного доклада аспиранта и т. д. Решать подобные задачи призвана квалиметрия.

Квалиметрия – научная дисциплина, в рамках которой изучаются методология и проблематика комплексного количественного оценивания качества объектов любой природы (одушевлённых или неодушевлённых; предметов или процессов; продуктов труда или продуктов природы) имеющих материальный или духовный характер, имеющих искусственное или естественное происхождение [9].

Объектом квалиметрии может любой целостный объект, который может быть изучен, исследован и познан. Предметом квалиметрии является оценка качества в количественном его выражении.

Квалиметрия подразделяется на:

-  общую квалиметрию или общую теорию квалиметрии, в которой рассматриваются проблемы и вопросы, а также методы измерения и оценивания качеств;

-  специальные квалиметрии больших группировок объектов: продукции, процессов, услуг, социального обеспечения, среды обитания и т. д.;

-  предметные квалиметрии отдельных видов продукции, процессов и услуг, такие как квалиметрия машиностроительной продукции, строительных объектов, квалиметрия нефтепродуктов, труда, образования и т. д.

Целью квалиметрии является разработка и совершенствование методик, с помощью которых качество конкретного оцениваемого объекта может быть выражено одним числом.

Существуют и ограниченные представления о качестве, когда оно оценивается не по всем, а по одному или по нескольким важнейшим для людей характеристикам объекта (рис.58).

Рис.58. Алгоритм оценки качества

Результат квалиметрического метода обычно представляется в относительной шкале. Оценка качества объекта осуществляется через его свойства, проходя через следующие этапы:

-  определение показателей, характеризующих перечень тех свойств, совокупность которых в полной мере характеризует качество;

-  формирование критериев, определяющих диапазон значений показателей, в котором они считаются допустимыми;

-  измерение этих показателей (их численных значений);

-  сопоставление полученных данных с критериями, т. е. характеристиками другого объекта, принимаемого за образец или эталон качества.

Полученный результат с определённой степенью достоверности может характеризовать качество исследуемого объекта.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8