Система управления – систематизированный набор средств влияния на подконтрольный объект для достижения определённых целей данным объектом. Объектом системы управления могут быть как технические объекты, так и люди. Объект системы управления может состоять из других объектов, которые могут иметь постоянную структуру взаимосвязей [9].

Системы управления с участием людей как объектов управления зачастую называют системами менеджмента.

Объектом управления может быть любая динамическая система или её модель. Состояние объекта характеризуется некоторыми количественными величинами, изменяющимися во времени, то есть переменными состояния. В естественных процессах в роли таких переменных может выступать температура, плотность определенного вещества в организме, курс ценных бумаг и т. д. Для технических объектов это механические перемещения (угловые или линейные) и их скорость, электрические переменные, температуры и т. д. Анализ и синтез систем управления проводится методами специального раздела математики – теории управления.

Управление можно разделить на два вида:

-  стихийное: воздействие происходит в результате взаимодействия субъектов (синергетическое управление);

-  сознательное: планомерное воздействия объекта (иерархическое управление).

При иерархическом управлении цель функционирования системы задается её надсистемой.

Системы управления разделяют на два больших класса:

-  автоматизированные системы управления (АСУ) – системы управления с участием человека в цикле управления;

-  системы автоматического управления (САУ) – системы управления без участия человека в цикле управления.

В зависимости от описания переменных, системы автоматического управления делятся на линейные и нелинейные. К линейным относятся системы, состоящие из элементов описания, которые задаются линейными алгебраическими или дифференциальными уравнениями.

В зависимости от природы управляемых объектов можно выделить биологический, экологический, экономические и технические системы управления. В качестве примеров технического управления можно привести:

-  системы дискретного действия или автоматы (торговые, игровые, музыкальные);

-  системы стабилизации уровня звука, изображения или магнитной записи или управляемые комплексы летательных аппаратов, включающие в свой состав системы автоматического управления двигателя, рулевыми механизмами, автопилоты и навигационные системы и т. д.

Автоматизированная система управления – совокупность математических методов, технических средств и организационных комплексов, обеспечивающих рациональное управление сложным объектом или процессом в соответствии с заданной целью.

В составе автоматизированных систем управления выделяют:

-  основную часть, в которую входят информационное, техническое и математическое обеспечение;

-  функциональную часть, к которой относятся взаимосвязанные программы, автоматизирующие конкретные функции управления.

Система управления общественным производством, составная часть управления народным хозяйством, представляет собой совокупность подсистем, отражающих отдельные стороны управления: цели, функции, принципы, методы, органы, кадры, технику и технологию. Предназначена для выработки и осуществления управляющего воздействия на производство в соответствии с объективными законами общественного развития.

Управление в системе – внутренняя функция системы, осуществляемая в системе независимо от того, каким образом, какими элементами системы она должна выполняться (см. рис.30).

Рис.30. Схема управления системой

По способу управления системы делятся на:

-  управляемые извне системы (без обратной связи, регулируемые, управляемые структурно, информационно или функционально);

-  управляемые изнутри (самоуправляемые или саморегулируемые – программноуправляемые, регулируемые автоматически, адаптируемые – приспосабливаемые с помощью управляемых изменений состояний и самоорганизующиеся – изменяющие во времени и в пространстве свою структуру наиболее оптимально, упорядочивающие свою структуру под воздействием внутренних и внешних факторов);

-  с комбинированным управлением (полуавтоматические, автоматические, автоматизированные, организационные).

4.5. Управление в организационных системах

4.5.1. Организационные системы

Теория управления организационными системами – раздел теории управления, изучающий механизмы функционирования организационных систем. Теория организации изучает принципы, законы и закономерности для создания, функционирования, развития и ликвидации организаций [37].

Организация – это целевое объединение ресурсов. Организации, созданные человеком (людьми), характеризуются наличием человека как активного ресурса. Организация – это группа людей, работающих совместно, во главе с руководителем и выполняющих определенные планы [9].

Организация может рассматриваться как процесс либо как явление. Как процесс организация – это совокупность действий, ведущих к образованию и совершенствованию взаимосвязей между частями целого. Как явление организация – это объединение элементов для реализации программы или цели и действующих на основании определенных правил и процедур.

Организационные отношения – это взаимодействие или противодействие между элементами организации внутри и вне ее при создании, функционировании, развитии и разрушении организации. Соответственно, они бывают трех уровней – здравого смысла, взаимного уничтожения, заранее спроектированного взаимодействия.

Внешняя среда включает условия и организации, в т. ч. политические, экономические и экологические условия; конкурирующие организации, поставщиков и потребителей, социальную инфраструктуру и т. д.

Общие черты организаций:

-  наличие по крайней мере одного человека;

-  наличие хотя бы одной цели, направленной на удовлетворение потребностей или интереса человека или общества;

-  получение прибавочного продукта в различных формах (материальной, духовной, информационной).

Каждая организация должна обладать признаками системы. Выпадание хотя бы одного из них неизбежно приводит организацию к ликвидации.

4.5.2. Организационное управление и управление в технике

Организационное управление принято противопоставлять управлению сложными техническими системами. Однако существуют отличия организационного управления от управления техническими объектами:

-  способность человека, как основного элемента организационной системы, к самостоятельному целеполаганию;

-  способность человека самостоятельно выбирать действия, отклоняясь от предписанного алгоритма поведения;

-  способность человека разрешать интеллектуальные задачи, которые обычно невозможно решить при помощи технических систем;

-  способность человека к рефлексии относительно собственной деятельности и деятельности других субъектов, в том числе – возможность прогнозирования их поведения.

Задачи управления людьми и коллективами решаются в рамках различных научных школ управления организационным поведением. В состав типичных задач входят: обеспечение необходимой мотивации исполнителей, согласованная с ними выработка управленческих решений, рациональное распределение ограниченных ресурсов в условиях неопределенности и т. п.

Регламентация управленческой деятельности осуществляется с помощью механизмов управления – процедур принятия управленческих решений.

Система управления организации представляет собой совокупность элементов, подсистем и коммуникаций между ними, а также процессов, обеспечивающих заданное функционирование организации. Она состоит из следующих компонент: методологии, структуры, процесса и техники управления.

Методология управления включает в себя – цели, законы и принципы, функции, методы, технологии управления и практику управленческой деятельности.

Процесс управления представляет собой – систему коммуникаций, разработку и реализацию управленческих решений, информационное обеспечение.

Структура управления включает в себя – функциональную и организационную структуру, схему организационных отношений, конкретные схемы взаимодействия высших органов управления и профессионализм персонала.

Техника управления включает – компьютерную и организационную технику, офисную мебель, сети связи, систему документооборота.

Методология и процесс управления формируют управленческую деятельность, а структура и техника управления – механизм управления.

Основная задача системы управления – формирование профессиональной управленческой деятельности, которая может рассматриваться как процесс и как явление [16].

4.6. Контрольные вопросы

1)  Что такое управление?

2)  Какие основные виды управления Вы знаете?

3)  В чём состоит принцип разомкнутого управления?

4)  В чём состоит принцип компенсации?

5)  Где применяется принцип управления по возмущения?

6)  Чем адаптивное управление отличается от оптимального?

7)  Каковы особенности интеллектуального управления?

8)  Что такое система управления?

9)  Чем автоматизированные системы управления отличаются от систем автоматического управления?

10)  Что такое организация?

11)  Чем отличается управление в организационных и технических системах?

5. Моделирование

Моделирование является одним из важнейших элементов системного анализа. Различные методы моделирования могут использоваться как на этапе анализа системы, так и на этапе синтеза знаний о ней. Более того, моделирование широко используется при рационализации.

5.1. Основные понятия моделирования

Процесс моделирования возможен благодаря замечательным системным закономерностям, связанным с морфологическим сходством систем различной природы. Эти закономерности раскрываются через ряд понятий, характеризующих различные степени подобия систем:

1)  Изоморфизм подразумевает одинаковость структуры систем. При этом различный смысл системообразующих отношений и различие элементов системы при их сопоставлении не учитываются. Две системы изоморфны, если между ними установлено такое взаимнооднозначное соответствие, что соответствующие друг другу объекты обладают соответствующими свойствами и находятся (внутри каждой системы) в соответствующих отношениях между собой. Две ели в лесу изоморфны (рис.31).

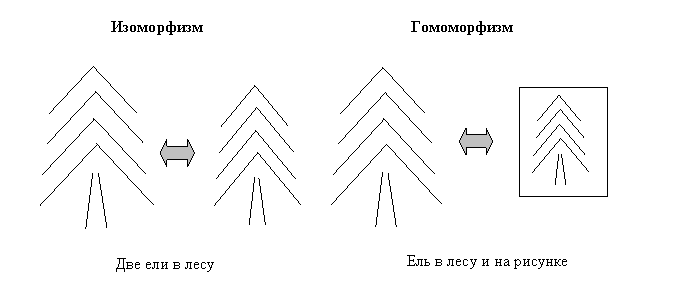
Рис.31. Примеры изоморфизма и гомоморфизма

Две лабораторных работы по одной дисциплине, выполняемые по общей методике разными преподавателями, можно считать изоморфными.

Создание изоморфных моделей сложная и, часто, бесполезная задача, поскольку упрощения, которое предполагается при моделировании, использование таких моделей может и не дать.

Отметим, что морфологией системы называется зафиксированная в пространстве, наблюдаемая, физически реализуемая совокупность элементов структуры системы.

2)  Гомоморфизм представляет собой такое соответствие между двумя системами, которое не является взаимно однозначным. При гомоморфизме аналогия между двумя системами меньше, чем при изоморфизме, и одна из систем является как бы упрощенной копией другой. Например, географическая карта является упрощенной копией по отношению к местности, а лабораторная установка является упрощённой копией производственного оборудования.

3)  Симметрия обозначает неизменность структуры системы относительно её преобразований. Симметрия подразумевает одинаковость структуры, но не формы.

Например, сферическая симметрия тела означает, что вид тела не изменится, если его вращать в пространстве на произвольные углы (сохраняя одну точку на месте) [9].

Отсутствие или нарушение симметрии называется асимметрией.

Понимание взаимосвязей между описанными понятиями, характеризующими подобие систем, позволяет моделировать объекты, явления и процессы окружающего мира.

Модель – образ или образец объекта, явления или процесса, используемый с некоторой целью, при определённых условиях в качестве его «заместителя». Модель может быть изоморфной, гомоморфной или полиморфной по отношению к моделируемой системе. Чаще всего используют гомоморфные модели (рис.32).

Например, моделью учебного процесса подготовки бакалавра в определённом аспекте можно считать учебный план.

Моделирование – исследование объектов познания на их моделях, а также построение и изучение моделей реально существующих объектов, явлений, процессов и конструируемых объектов (систем) для определения, уточнения их характеристик, рационализации способов их построения и т. п.

Моделировать можно как целые объекты, или системы, так и их аспекты, элементы или подсистемы.

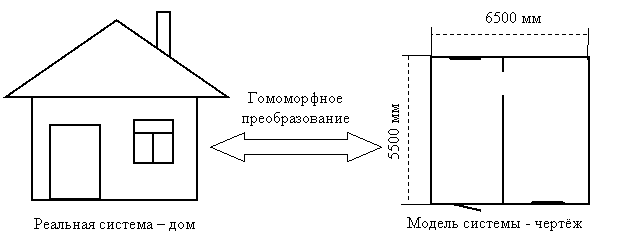
Рис.32. Пример модели

Для каждой модели существует область применимости (предметная область) – набор объектов и свойств, которые адекватно описываются моделью. Следовательно, применение каждой модели ограничено и для исследования сложного объекта требуется использование нескольких моделей (рис.33). Такой подход называется принципом дополнительности Нильса Бора [15].

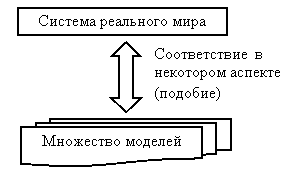
Рис.33. Связь системы и её моделей

Более емкое и удобное в системном анализе определение:

Модель системы – определённое формализованное представление, служащее для ответа на вопросы, заданные относительно реальной системы.

5.2. Принципы моделирования

Рассмотрим принципы, которым должна удовлетворять правильно построенная модель:

1)  Принцип адекватности предусматривает соответствие модели реальной системе и целям исследования по уровню сложности и организации (рис.34). Качество и ценность модели определяется тем, насколько правильно и адекватно модель отображает исследуемую реальную систему.

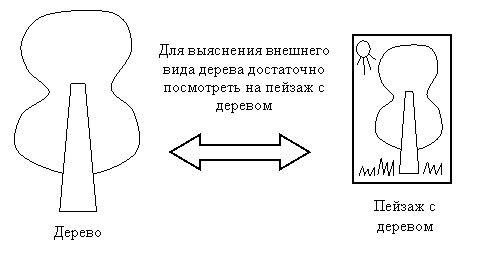
Рис.34. Пример выполнения принципа адекватности

Возвращаясь к примеру учебного плана, следует отметить, что его адекватность означает учёт физической возможности для проведения в нужном объёме планируемых лекционных и лабораторных занятий.

2)  Принцип предметности модели состоит в том, что модель стро­ится для решения только строго определенного вида задач или отдельной задачи. Создание универсальной модели для решения большого числа задач – сложная, часто не разрешимая задача, поскольку универсальные модели либо не конкретны и годятся для решения только описательных задач, либо слишком сложны.

Например, учебный план составляется только для одного профиля и определённой формы обучения и не применяется для других.

Этот принцип тесно связан с принципом адекватности, дополняя его.

3)  Принцип разумного упрощения проявляется следующим образом: модель должна быть проще и, обычно, дешевле прототи­па. Модель должна делать систему понятнее для исследователя, а это достигается упрощением отдельных её аспектов. В моделируемой системе умышленно утрируются важные для исследователя и игнорируются второстепенные, менее существенные свойства (рис.35).

Учебный план гораздо проще учебного процесса, который на нём основан.

Рис.35. Пример моделей предприятия в разных срезах

4)  Принцип соответствия сложности модели. Модели по своей природе всегда носят приближенный характер, поэтому важно выяснить степень этого приближения. При моделировании решаются две противоположные задачи: детализация системы и снижение сложности её модели.

Благодаря большому опыту планирования учебного процесса форма учебного плана обычно является эффективной.

Практическими рекомендациями по умень­шению сложности моделей являются:

-  уменьшение числа переменных параметров, достигаемое исключе­нием и объединением несущественных переменных;

-  изменение природы переменных параметров, т. е. переход от динамических параметрам к статическим, от непрерывных – к дискретным и т. д.;

-  изменение функциональной зависимости между переменными от нелинейной к линейной, от непрерывной к дис­кретной и т. п.;

-  добавление, исключение или мо­дификация ограничений;

-  снижение точности модели с учётом того, что точность результатов мо­делирования не может быть выше точности исходных данных.

5)  Принцип блочного строения предполагает выделение структуры в моделях. При соблюдении принципа блочного строения облегчается разработка сложных моделей и появляется возможность использования накопленного опыта и готовых бло­ков с минимальными связями между ними при создании новых моделей. Выделение блоков производится с учетом разделения модели по этапам и режимам функционирования системы.

Применительно к учебному плану принцип блочного строения означает возможность выделения приложений, таких как «график учебного процесса», «перечень дисциплин по выбору», «перечень факультативных дисциплин».

Для решения реальных задач рассмотренные выше принципы следует спользовать на различных уровнях моделирования [7]:

1)  Концептуальный уровень, на котором определяются границы системы, т. е. её базовые входы и выходы.

2)  Топологический уровень, на котором определяются связи входных, выходных и внутренних переменных системы (моделями данного уровня являются графы или сети).

3)  Структурный уровень, на котором определяется структура операторов, описывающих взаимосвязь входных, выходных и внутренних переменных. При этом взаимосвязь может задаваться функциональными статическими соотношениями, операторами описания динамики, матричными преобразованиями и т. д.

4)  Параметрический уровень, на котором задаются параметры операторов связей, обеспечивая полную определённость модели данного уровня (в той степени, в которой определены параметры), благодаря чему и над моделью могут проводиться наиболее информативные эксперименты и выполняться расчеты.

5.3. Виды моделирования

Существует множество подходов к классификации видов моделирования (рис.36). Рассмотрим один из наиболее подробных:

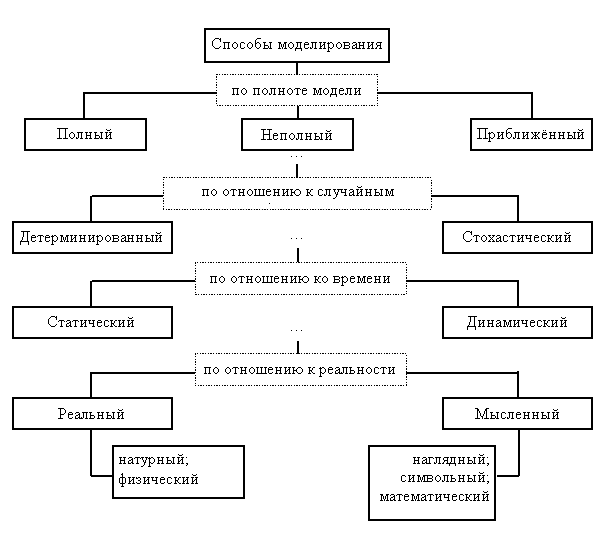
Рис.36. Классификация способов моделирования

По полноте способы моделирования делятся на: полный, неполный и приближенный. При полном способе моделирования модели изоморфны (идентичны) объекту во вре­мени и пространстве. Для неполного способа моделирования эта идентич­ность не сохраняется. В основе приближенного способа моделирования лежит подобие, при котором некоторые стороны реального объекта не моделируются совсем (гомоморфизм). Поскольку абсолютное подобие возможно лишь при замене одного объекта другим точно таким же, то при моделировании абсолютное подобие не имеет места. Исследователи стремятся к тому, чтобы модель хорошо отображала только исследуемый аспект системы.

По отношению к случайностям среди способов моделирования выделяют детерминированный и стохастический.

Детерминированное моделирование отображает процессы, в которых случайные воздействия не учитываются. Стохастический способ их учитывает.

По отношению ко времени способы разделились на статические и динамические (рис.37). Статический способ моделирования служит для опи­сания объекта и его состояния в определённый момент времени (в статике), а динамический способ – для исследования изменения рассматриваемого объекта или процесса с течением времени.

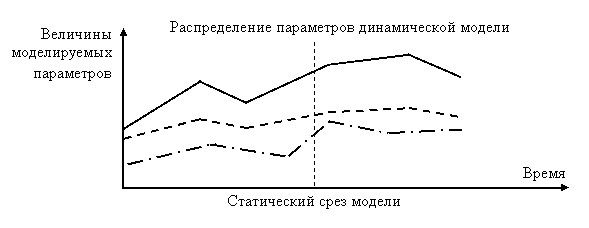
Рис.37. Взаимосвязь статических и динамических моделей

По отношению к тому, является ли генератором и носителем модели сознание человека способы моделирования подразделены на мысленный и реальный.

При реальном способе моделировании ис­следуются характеристики либо на реальном объекте целиком, либо на его части. Такие исследования проводятся как на объек­тах, работающих в нормальных режимах, так и при организации специальных режимов для оценки интересующих исследователя характеристик. Реальное моделирование яв­ляется наиболее адекватным, но его возможности ограничены. Натурным способом моделирования называют проведение исследова­ния на реальном объекте с последующей обработкой и анализом результа­тов эксперимента. Физический способ, отличающееся от натурного тем, что исследование проводится на оборудовании, сохраняющем физическое подобие реального процесса. При этом варьируются характеристики внешней среды и исследует­ся поведение самого объекта или его модели. Физическое моделирование может протекать в реальном, модельном масштабах времени или рассматри­ваться без учета времени. В последнем случае изучению подле­жат статические процессы, рассматриваемые на определённый момент времени.

Мысленный способ моделирования является, пожалуй, самым старым. Он позволяет сформировать модели, не реализуемые в данный момент времени, при текущем уровне развития науки и технологий. Благодаря этому мысленный способ позволяет создавать самые смелые, но и самые сложные для принятия на них решения модели. Мысленный способ моделирования делится на наглядный, символический и математический способы. Наглядное моделирование широко используется в учебном процессе. Он состоит в создании наглядных модели на базе представлений чело­века о реальных объектах, для отобра­жения протекающих в них явлений и процессов.

Символический способ моделирования заключается в создании определённого логического объекта, который замещает реальный и выражает его основные свойства с помощью системы символов и знаков.

Математический способ моделирования устанавливает в соответствие реальному объекту некоторый математи­ческий объект, называемый математической моделью. Для исследования характеристик любой системы матема­тическими методами, должна быть обяза­тельно проведена её формализация и построена математическая модель. Вид математической модели зависит как от природы реального объекта, так и от задач исследования объекта, от требуемой достоверности и точности решения зада­чи. Математическая модель описыва­ет реальный объект с некоторой степенью приближения.

5.4. Характеристика известных способов моделирования

Наиболее распространённые способы моделирования включают:

1)  Аналитическое моделирование связано с моделированием функционального аспекта системы (рис.38). При этом закон функционирования системы записывается в виде аналитических уравнений (алгебраических, интегральных, дифференциальных, разностных и т. д.).

Рис.38. Схема аналитического моделирования

Распространены компьютерные методы исследования функционирования систем. Они сводятся к построению соответствующего алгоритма для реализации математической модели на компьютере.

2)  Имитационное моделирование служит для воспроизведения алго­ритма функционирования (поведения) системы во времени. При этом имитируются явления и операции, составляющие процесс, с сохранением их логической связи и последова­тельности протекания, что позволяет полу­чать динамическое описание процесса. Основное преимущество имитационного моделирования над аналитическим – возможность решения бо­лее сложных задач. Имитационные модели позволяют учитывать такие факторы, как наличие дискретных и непрерывных элементов, нелинейные характеристики элементов системы, многочисленные случайные воздействия и т. п. В настоящее время имитационное моделирование – один из наиболее эффективных методов исследования систем (рис.39).

Метод имитационного моделирования применяется для оцен­ки вариантов структуры системы, эффективности различных ал­горитмов управления системой, влияния изменения различных параметров системы. Имитационное моделирование положено в основу структурного, алгоритмического и парамет­рического синтеза систем, если требуется создать систему с нужными характеристиками при определенных ограничениях.

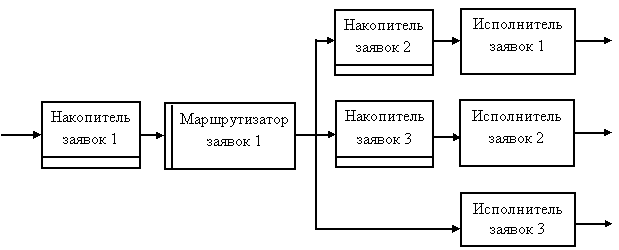
Рис.39. Пример простой имитационной модели (схемы системы массового обслуживания)

3)  Комбинированное (аналитико-имитационное) моделирование позволяет объединить достоинства аналитического и имитаци­онного моделирования. При построении комбинированных мо­делей производится предварительная декомпозиция процесса функционирования объекта на составляющие подпроцессы, и для тех из них, где это возможно, используются аналитические модели, а для остальных подпроцессов строятся имитационные моде­ли. Такой подход дает возможность охватить качественно новые классы систем, которые не могут быть исследованы с использо­ванием аналитического или имитационного моделирования в отдельности.

4)  Ситуационное моделирование основывается на модельной тео­рии мышления, используемой для описания основных ме­ханизмов регулирования при принятии решений. Оно опирается на представление о формиро­вании в мозге человека информационной модели наблюдаемого им мира. Согласно этому представлению, механизм по­ведения человека базируется на формировании целевой ситуа­ции (модели результата) и мысленного преобразования имеющейся фактически ситуации в желаемую (целевую). Ситуационная модель является описанием объекта в виде совокупности элементов, связанных между собой определенны­ми отношениями, отображающими семантику предметной области. Она имеет многоуровневую структуру и пред­ставляет собой описание смысла процессов управления протекающих в системе.

5)  Структурное моделирование. Системный анализ базирует­ся на особенностях структур опреде­ленного вида, которые используются как средство исследования систем или служат для разработки на их основе специальных подходов к моделированию с применением других методов фор­мализованного представления систем. Развитием структур­ного моделирования являются объектно-ориентированное и функциональное моде­лирование.

6)  Кибернетическое моделирование опирается на модели процессов, не являющиеся подобиями реальных процессов. Процесс моделирования состоит в представлении реального объекта как «чер­ного ящика», получающего ресурсы на входы и передающего результаты на выходы, и описании модели как функции, связывающей выходами с входами, без учета знаний о топологии системы. В осно­ве кибернетических моделей лежит отраже­ние информационных процессов управления, на основе которых можно оценить поведение реального объекта.

Между рассмотренными способами моделирования имеется взаимосвязь. Они могут взаимно преобразовываться и дополнять друг друга. Рассмотрим применение этих моделей в рамках единой методологии моделирования бизнес-процессов, используемой при разработке информационных систем (см. [17]).

5.5. Теория игр и принятие решений

Классическими задачами системного анализа являются игровые задачи принятия решений в условиях риска и неопределенности.

Неопределенными могут быть как цели операции, условия выполнения операции, так и сознательные действия противников или других лиц, от которых зависит успех операции.

Разработаны специальные математические методы, предназначенные для обоснования решений в условиях риска и неопределенности. В некоторых, наиболее простых случаях эти методы дают возможность фактически найти и выбрать оптимальное решение. В более сложных случаях эти методы доставляют вспомогательный материал, позволяющий глубже разобраться в сложной ситуации и оценить каждое из возможных решений с различных точек зрения, и принять решений с учетом его возможных последствий. Одним из важных условий принятия решений в этом случае является минимизация риска.

При решении ряда практических задач исследования операций (например, в области экологии или обеспечения безопасности жизнедеятельности) приходится анализировать ситуации, в которых сталкиваются несколько враждующих сторон, преследующих различные цели, причем результат любого мероприятия каждой из сторон зависит от того, какой образ действий выберет противник. Такие ситуации мы можно отнести к конфликтным ситуациям.

Теория игр – математический метод изучения оптимальных стратегий в играх. Под игрой понимается процесс, в котором участвуют две и более сторон, ведущих борьбу за реализацию своих интересов. Каждая из сторон имеет свою цель и использует некоторую стратегию, которая может вести к выигрышу или проигрышу – в зависимости от поведения других игроков [9].

Результат игры (выигрыш или проигрыш) не всегда имеет количественное выражение, но обычно можно, хотя бы условно, выразить его числовым значением.

Ход – выбор одного из предусмотренных правилами игры действий и его осуществление. Ходы делятся на личные и случайные. Личным ходом называется сознательный выбор игроком одного из возможных вариантов действий и его осуществление. Случайным ходом называется выбор из ряда возможностей, осуществляемый не решением игрока, а каким-либо механизмом случайного выбора (бросание монеты, выбор карты из перетасованной колоды и т. п.). Для каждого случайного хода правила игры определяют распределение вероятностей возможных исходов. Игра может состоять только их личных или только из случайных ходов, или из их комбинации. Следующим основным понятием теории игр является понятие стратегии. Стратегия – это априори принятая игроком система решений (вида «если – то»), которых он придерживается во время ведения игры, которая может быть представлена в виде алгоритма и выполняться автоматически.

Целью теории игр является выработка рекомендаций для разумного поведения игроков в конфликтной ситуации, т. е. определение «оптимальной стратегии» для каждого из них. Стратегия, оптимальная по одному показателю, необязательно будет оптимальной по другим. Сознавая эти ограничения, можно использовать математический аппарат теории игр для выработки, если не в точности оптимальной, то, во всяком случае «приемлемой» стратегии.

Игры можно классифицировать: по количеству игроков, количеству стратегий, характеру взаимодействия игроков, характеру выигрыша, количеству ходов, состоянию информации и т. д. [19].

В зависимости от количества игроков различают игры двух и n игроков. Первые из них наиболее изучены. Игры трёх и более игроков менее исследованы из-за возникающих принципиальных трудностей и технических возможностей получения решения.

В зависимости от числа возможных стратегий игры делятся на «конечные» и «бесконечные».

Игра называется конечной, если у каждого игрока имеется только конечное число стратегий, и бесконечной, если хотя бы у одного из игроков имеется бесконечное число стратегий.

По характеру взаимодействия игры делятся на бескоалиционные: игроки не имеют права вступать в соглашения, образовывать коалиции; коалиционные (кооперативные) – могут вступать в коалиции.

В кооперативных играх коалиции заранее определены.

По характеру выигрышей игры делятся на: игры с нулевой суммой (общий капитал всех игроков не меняется, а перераспределяется между игроками; сумма выигрышей всех игроков равна нулю) и игры с ненулевой суммой.

По виду функций выигрыша игры делятся на: матричные, биматричные, непрерывные, выпуклые и др.

Матричная игра – это конечная игра двух игроков с нулевой суммой, в которой задаётся выигрыш игрока 1 в виде матрицы (строка матрицы соответствует номеру применяемой стратегии игрока 1, столбец – номеру применяемой стратегии игрока 2; на пересечении строки и столбца матрицы находится выигрыш игрока 1, соответствующий применяемым стратегиям).

Для матричных игр доказано, что любая из них имеет решение и оно может быть легко найдено путём сведения игры к задаче линейного программирования.

Биматричная игра – это конечная игра двух игроков с ненулевой суммой, в которой выигрыши каждого игрока задаются матрицами отдельно для соответствующего игрока (в каждой матрице строка соответствует стратегии игрока 1, столбец – стратегии игрока 2, на пересечении строки и столбца в первой матрице находится выигрыш игрока 1, во второй матрице – выигрыш игрока 2.)

Непрерывной считается игра, в которой функция выигрышей каждого игрока является непрерывной. Доказано, что игры этого класса имеют решения, однако не разработано практически приемлемых методов их нахождения.

Если функция выигрышей является выпуклой, то такая игра называется выпуклой. Для них разработаны приемлемые методы решения, состоящие в отыскании чистой оптимальной стратегии (определённого числа) для одного игрока и вероятностей применения чистых оптимальных стратегий другого игрока. Такая задача решается сравнительно легко.

5.6. Моделирование бизнес-процессов

Бизнес-процесс – это процесс преобразования информационных и управленческих потоков в организованной системе с некоторой целью, реализуемый неоднократно и находящийся под управлением.

Основу моделирования бизнес-процессов организационных систем составляет их вербализация, т. е. описание при помощи слов естественного языка. Оно может быть получено методами анкетирования или интервьюирования экспертов, с помощью изучения нормативных документов или другими способами. Такое описание неструктурированно и поэтому малопригодно для формирования каких-либо существенных выводов о свойствах и параметрах бизнес-процесса, но оно необходимо для того, чтобы сформированные модели были адекватны предметной области (рис.40).

Например, для выпускающей кафедры с помощью текста можно указать перечень специальностей, описать научные лаборатории и даже попытаться описать основные выполняемые функции. Но обеспечить системность такого изложения будет очень сложно.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8