Основные определения и понятия теории моделирования, области использования (стр. 5 )

вероятность загрузки системы:

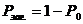
вероятность отказа в обслуживании:

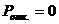, т. к. любая заявка будет рано или поздно обслужена

среднее число требований в очереди:

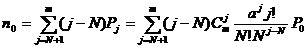
среднее время ожидания в очереди:

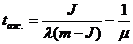
среднее число заявок в системе:

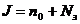, т. е. среднее число заявок в очереди плюс среднее число занятых каналов;

среднее число занятых каналов:

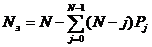
среднее время пребывания требования в системе:

.

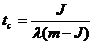4. СМО с «взаимопомощью» между каналами

СМО с «взаимопомощью» - системы, в которых одна и та же заявка может обслуживаться несколькими каналами. Взаимопомощь может быть организована в любом типе СМО (замкнутая, разомкнутая).

При анализе таких СМО необходим учет 2-х факторов:

1.  Насколько убыстряется дисциплина обслуживания заявки при работе нескольких каналов. Самый простой вариант – пропорциональное увеличение: , где k – число каналов, занятых обслуживанием заявки.

2.  Дисциплина взаимопомощи. Самый простой вариант – «все как один». Заявку обслуживают сразу все каналы.

Выгодно или нет вводить «взаимопомощь» зависит от реальной СМО и ее параметров.

Пример. Трехканальная СМО с потерями и бесконечным потоком заявок на входе.

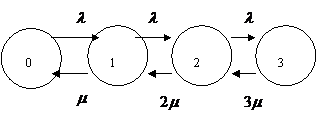Размеченный граф состояний для СМО без «взаимопомощи»

Размеченный граф состояний для системы с «взаимопомощью»

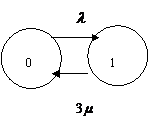Далее, для нахождения предельных вероятностей состояний, необходимо составить систему уравнений Колмогорова.

5. СМО с ошибками в обслуживании

Заявка, принятая к обслуживанию, обслуживается не с полной достоверностью, а с некоторой вероятностью – р.

Например, справочное бюро не всегда выдает верные справки; корректор может неверно исправить ошибку, телефонная станция не всегда соединяет абонента с нужным номером и т. д. Ошибки в обслуживании характерны для СМО, в которых каналом обслуживания является человек.

Учет вероятности верного обслуживания заявки производится следующим образом: интенсивность обслуживания умножается на вероятность обслуживания заявки

Пример. Размеченный граф состояний для трехканальной СМО с ошибками в обслуживании.

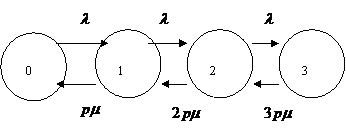
Далее, для нахождения предельных вероятностей состояний, необходимо составить систему уравнений Колмогорова.

Еще одна разновидность СМО с ошибками в обслуживании – характер обслуживания зависит от длины очереди. При увеличении длины очереди канал начинает «спешить». Время обслуживания уменьшается, но увеличивается вероятность ошибки в обслуживании.

Интенсивность обслуживания в этом случае вычисляется по формул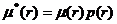е: , где

- интенсивность обслуживания при длине очереди r;

- вероятность обслуживания заявки при длине очереди r.

Пример. Размеченный граф состояний для одноканальной СМО с ограниченной длиной очереди равной 2, с ошибками в обслуживании в зависимости от длины очереди.

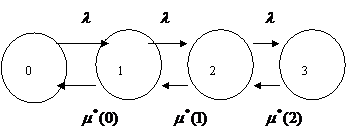11. Инструментальные средства моделирования

11.1. Классы инструментальных средств

Универсальным инструментальным средством создания моделей являются языки программирования общего пользования (Pascal, C/C++ и др.). На основе этих языков в настоящее время бурное развитие получили средства визуального проектирования программ (Delphi, Visual C++), облегчающие выполнение некоторых трудоемких операций, например, создание интерфейса программы. Наряду с этим существует множество специализированных средств моделирования, позволяющих быстрее и с меньшими затратами (по сравнению с универсальными языками программирования) создавать и исследовать модели. В развитии специализированных средств можно выделить два направления:

1. Средства моделирования для анализа достаточно широкого класса систем. К ним относятся языки имитационного моделирования (GPSS, SIMSCRIPT и др.), пакеты прикладных программ, использующих для моделирования аналитические методы, такие как MathCad, MathLab, SAS, Statistica и др. Основным недостатком этих средств является то, что их применение требует от исследователя специальной подготовки.

2. Программные комплексы, специализирующиеся на моделировании узкого круга систем одной конкретной предметной области. Недостаток, заключающийся в ограниченности применения таких программ одной предметной областью, с лихвой покрывается такими преимуществами, как легкость их освоения специалистами в данной предметной области, и эффективность применения, являющаяся следствием узкой специализации.

Подробнее рассмотрим специфику инструментальных средств имитационного моделирования. Как было ранее отмечено, существует два направления их развития. Первое из них представляют языки имитационного моделирования. Эти языки по сравнению с универсальными языками программирования снижают трудоемкость написания моделирующих программ, включают специализированные процедуры, которые могут применяться в любой имитационной модели, и отличаются точностью выражения понятий, характеризующих имитируемые процессы, и автоматическим формированием определенных типов данных, необходимых в процессе имитационного моделирования.

11.2. Технология разработки имитационной модели

Процесс последовательной разработки имитационной модели начинается с создания простой модели, которая затем постепенно усложняется в соответствии с предъявляемыми решаемой проблемой требованиями. В каждом цикле создания программной модели можно выделить следующие этапы:

1.  Формулирование проблемы: описание исследуемой проблемы, установление границ и ограничений моделируемой системы, определение целей исследования.

2.  Разработка модели: переход от реальной системы к некоторой логической схеме (абстрагирование).

3.  Подготовка данных: отбор данных, необходимых для построения модели, и представление их в соответствующей форме.

4.  Трансляция модели: описание модели на языке имитационного моделирования.

5.  Оценка адекватности: повышение до приемлемого уровня степени уверенности, с которой можно судить относительно корректности выводов о реальной системе, полученных на основании обращения к модели.

6.  Планирование: определение условий проведения машинного эксперимента с имитационной моделью.

7.  Экспериментирование: многократный прогон имитационной модели на компьютере для получения требуемой информации.

8.  Анализ результатов: изучение результатов имитационного эксперимента для подготовки выводов и рекомендаций по решению проблемы.

9.  Реализация и документирование: реализация рекомендаций, полученных на основе имитации, и составление документации по модели и ее использованию.

11.3. Моделирование работы вычислительной системы в среде GPSS/World

Задача. К компьютеру на обработку поступают задания. Из предварительного обследования получена информация, что интервал времени между двумя последовательными поступлениями заданий к компьютеру подчиняется равномерному закону распределения в интервале (1-11 мин.). Перед компьютером допустима очередь заданий, длина которой не ограничена. Время выполнения задания также равномерно распределено в интервале (1-19 мин.). Смоделировать обработку 100 заданий.

В среде GPSS программа, моделирующая работу вычислительной системы, выглядит следующим образом:

GENERATE 360,300

SEIZE B

ADVANCE 600,540

RELEASE B

TERMINATE 1

START 100

Единица модельного времени задана 1 секунда.

Так как время среднее время обработки задания больше, чем среднее время поступления задания, в вычислительной системе будет накапливаться очередь с течением времени. Для сбора статистики об очереди используются операторы QUEUE, DEPART. В этом случае программа выглядит следующим образом:

GENERATE 360,300

QUEUE BR

SEIZE B

DEPART BR

ADVANCE 600,540

RELEASE B

TERMINATE 1

START 100

Наберите эту программу в среде GPSS/World.

Студенческая версия GPSS/World не требует установки. Для запуска программы достаточно запустить на выполнение файл GPSSW. exe. После этого откроется среда моделирования GPSS/World. Далее необходимо выбрать пункт меню File/Open и в открывшемся диалоговом окне «Новый документ» - Создать Model. В результате будет открыто окно Untitled Model1, в котором необходимо набрать текст программы.

Файл с программой можно сохранить в файле с расширением. gps (пункты меню File/Save; File/Save As).

Для запуска программы на выполнение необходимо выбрать пункт меню Command/Create Simulation.

Приведем основные операторы, которые используются в программе.

1. Для создания транзактов (заявок), входящих в модель, служит блок GENERATE (генерировать), имеющий следующий формат:

GENERATE A,B,C,D,E

В поле A задается среднее значение интервала времени между моментами поступления в модель двух последовательных транзактов. Если этот интервал постоянен, то поле B не используется. Если же интервал поступления является случайной величиной, то в поле B указывается модификатор среднего значения, который может быть задан в виде модификатора-интервала или модификатора-функции.

Модификатор-интервал используется, когда интервал поступления транзактов является случайной величиной с равномерным законом распределения вероятностей. В этом случае в поле B может быть задан любой СЧА, кроме ссылки на функцию, а диапазон изменения интервала поступления имеет границы A-B, A+B.

Например, блок

GENERATE 100,40

создает транзакты через случайные интервалы времени, равномерно распределенные на отрезке [60;140].

Модификатор-функция используется, если закон распределения интервала поступления отличен от равномерного. В этом случае в поле B должна быть записана ссылка на функцию (ее СЧА), описывающую этот закон, и случайный интервал поступления определяется, как целая часть произведения поля A (среднего значения) на вычисленное значение функции.

В поле C задается момент поступления в модель первого транзакта. Если это поле пусто или равно 0, то момент появления первого транзакта определяется операндами A и B.

Поле D задает общее число транзактов, которое должно быть создано блоком GENERATE. Если это поле пусто, то блок генерирует неограниченное число транзактов до завершения моделирования.

В поле E задается приоритет, присваиваемый генерируемым транзактам. Число уровней приоритетов неограниченно, причем самый низкий приоритет - нулевой. Если поле E пусто, то генерируемые транзакты имеют нулевой приоритет.

Транзакты имеют ряд стандартных числовых атрибутов. Например, СЧА с названием PR позволяет ссылаться на приоритет транзакта. СЧА с названием M1 содержит так называемое резидентное время транзакта, т. е. время, прошедшее с момента входа транзакта в модель через блок GENERATE. СЧА с названием XN1 содержит внутренний номер транзакта, который является уникальным и позволяет всегда отличить один транзакт от другого. В отличие от СЧА других объектов, СЧА транзактов не содержат ссылки на имя или номер транзакта. Ссылка на СЧА транзакта всегда относится к активному транзакту, т. е. транзакту, обрабатываемому в данный момент симулятором.

Задания для самостоятельной работы:

- Напишите сегмент модели, который моделирует поступление 14 транзактов с равномерным законом распределения (14-32);

- Смоделируйте приход в нулевой момент времени пяти транзактов с уровнем приоритета 25;

- Смоделируйте ситуацию, когда транзакты поступают в модель каждые 30-60 минут (первый появляется на 20-й минуте). Единица модельного времени 0,1 минута.

2. Для удаления транзактов из модели служит блок TERMINATE (завершить), имеющий следующий формат:

TERMINATE A

Значение поля A указывает, на сколько единиц уменьшается содержимое так называемого счетчика завершений при входе транзакта в данный блок TERMINATE. Если поле A не определено, то оно считается равным 0, и транзакты, проходящие через такой блок, не уменьшают содержимого счетчика завершений.

Начальное значение счетчика завершений устанавливается управляющим оператором START (начать), предназначенным для запуска прогона модели. Поле A этого оператора содержит начальное значение счетчика завершений. Прогон модели заканчивается, когда содержимое счетчика завершений обращается в 0. Таким образом, в модели должен быть хотя бы один блок TERMINATE с непустым полем A, иначе процесс моделирования никогда не завершится.

Текущее значение счетчика завершений доступно программисту через системный СЧА TG1.

Участок блок-схемы модели, связанный с парой блоков GENERATE-ТERMINATE, называется сегментом. Простые модели могут состоять из одного сегмента, в сложных моделях может быть несколько сегментов.

Например, простейший сегмент модели, состоящий всего из двух блоков GENERATE и TERMINATE и в совокупности с управляющим оператором START моделирует процесс создания случайного потока транзактов, поступающих в модель со средним интервалом в 100 единиц модельного времени, и уничтожения этих транзактов. Начальное значение счетчика завершений равно 1000. Каждый транзакт, проходящий через блок TERMINATE, вычитает из счетчика единицу, и таким образом моделирование завершится, когда тысячный по счету транзакт войдет в блок TERMINATE. При этом точное значение таймера в момент завершения прогона непредсказуемо. Следовательно, в приведенном примере продолжительность прогона устанавливается не по модельному времени, а по количеству транзактов, прошедших через модель.

GENERATE 100,40

TERMINATE 1

START 1000

Если необходимо управлять продолжительностью прогона по модельному времени, то в модели используется специальный сегмент, называемый сегментом таймера.

GENERATE 100,40

TERMINATE

GENERATE 100000

TERMINATE 1

START 1

Например, в модели из двух сегментов, первый (основной) сегмент выполняет те же функции, что и в предыдущем примере. Заметим, однако, что поле A блока TERMINATE в первом сегменте пусто, т. е. уничтожаемые транзакты не уменьшают содержимого счетчика завершений. Во втором сегменте блок GENERATE создаст первый транзакт в момент модельного времени, равный 100000. Но этот транзакт окажется и последним в данном сегменте, так как, войдя в блок TERMINATE, он обратит в 0 содержимое счетчика завершений, установленное оператором START равным 1. Таким образом, в этой модели гарантируется завершение прогона в определенный момент модельного времени, а точное количество транзактов, прошедших через модель, непредсказуемо.

В приведенных примерах транзакты, входящие в модель через блок GENERATE, в тот же момент модельного времени уничтожались в блоке TERMINATE.

Замечание: Не путайте ограничитель транзактов в блоке GENERATE и счетчик завершения. Ограничитель задает число транзактов, которые войдут в модель, а счетчик – число транзактов, которые выйдут из модели. По окончании моделирования транзакты могут оставаться в модели.

Задания для самостоятельной работы:

- Напишите сегмент программы, в котором моделирование заканчивается после того, как через модель пройдут 300 транзактов, транзакты должны поступать в модель каждые 21-29 ед. модельного времени;

- Задайте время моделирования работы системы 8 часов, единица модельного времени – 1 секунда.

3. Моделирование одноканальных устройств

Устройства используются при моделировании систем для имитации работы оборудования единичной емкости, например, процессор, кана­л передачи данных, человек, компьютер. Устройство в любой момент времени может обрабатывать только одно сообщение (транзакт). Если в процесс обслуживания появляется новый транзакт, то он должен:

- либо подождать своей очереди;

- либо направиться в другое место;

- либо прервать обслуживание текущего сообщения.

Для использования одноканального устройства транзакту необходимо выполнить следующие шаги.

Второй и четвертый шаги реализуются блоками SEIZE и RELEASE.

Блок SEIZE имеет следующий формат :

SEIZE A

Свободный блок SEIZE позволяет вошедшему в него сообщению занять указанное устройство. Блок SEIZE задерживает сообщение, если устройство занято или находится в состоянии недоступнос­ти.

В поле А задается номер (имя) занимаемого устройства.

Сообщение, занявшее уст­ройство, затем пытается перейти к следующему по номеру блоку. Уст­ройство остается занятым до тех пор, пока занимающее его сообщение не войдет в соответствующий блок RELEASE. Прежде чем освободить устройство, сообщение может пройти через неограниченное число блоков.

Блок RELEASE имеет следующий формат:

RELEASE A

Блок RELEASE предназначен для освобождения устройства тем со­общением, которым В поле А задается номер (имя) освобождаемого уст­ройства.

Транзакты обслуживаются устройствами в течение некоторого промежутка времени. Для моделирования такого обслуживания, т. е. для задержки транзактов на определенный отрезок модельного времени (реализация шага 3), служит блок ADVANCE (задержать), имеющий следующий формат:

ADVANCE A,B

Операнды в полях A и B имеют тот же смысл, что и в соответствующих полях блока GENERATE. Следует отметить, что транзакты, входящие в блок ADVANCE, переводятся из списка текущих событий в список будущих событий, а по истечении вычисленного времени задержки возвращаются назад, в список текущих событий, и их продвижение по блок-схеме продолжается. Если вычисленное время задержки равно 0, то транзакт в тот же момент модельного времени переходит в следующий блок, оставаясь в списке текущих событий.

Например, транзакты, поступающие в модель из блока GENERATE через случайные интервалы времени, имеющие равномерное распределение на отрезке [60;140], попадают в блок SEIZE и занимают устройство с номером 1. Далее в блоке ADVANCE определяется случайное время задержки транзакта, имеющее равномерное распределение на отрезке [30;130], и транзакт переводится в список будущих событий. По истечении времени задержки транзакт возвращается в список текущих событий и входит в блок RELEASE и освобождает устройство 1. Заметим, что в списке будущих событий, а значит и в блоке ADVANCE может одновременно находиться произвольное количество транзактов.

GENERATE 100,40

SEIZE 1

ADVANCE 80,50

RELEASE 1

В рассмотренных выше примерах случайные интервалы времени подчинялись равномерному закону распределения вероятностей. Для получения случайных величин с другими распределениями в GPSS используются вычислительные объекты: переменные и функции.

Задания для самостоятельной работы:

- Приведите фрагмент программы, который моделирует обработку детали на станке. Название устройства – MACHINE, время обработки – 10 ед. модельного времени.

- Напишите сегмент программы, который описывает процесс шлифования изделия. Шлифование занимает 3-5 минут, в каждый момент времени может обрабатываться только одно изделие. Единица модельного времени – 1 секунда.

4. Очереди. Блоки QUEUE и DEPART

В GPSS объекты типа "очередь" вводятся для сбора статисти­ческих данных.

Статистика об очередях собирается в моменты входа транзакта в блок QUEUE (вход в очередь) или в блок DEPART (выход из очереди).

Формат записи блока QUEUE:

QUEUE A,[B]

Блок QUEUE увеличивает длину очереди.

В поле А задается номер или имя очереди, к длине которой до­бавляются единицы. Операнд может быть именем, положительным целым, СЧА.

Поле В определяет число единиц, на которое увеличивается те­кущая длина очереди. Если поле В пусто, то прибавляется единица.

Когда сообщение входит в блок QUEUE, то ищется очередь с име­нем, определенным операндом А. Если необходимо, очередь создается.

Поскольку к очереди добавляются единицы, а не сами сообщения, не составляется список членов очереди. Сообщения в этот же момент условного времени пытаются перейти к следующему блоку.

Поскольку очередь обычно используется для измерения времени ожидания, за блоком QUEUE обычно следуют такой блок как SEIZE, который может задержать сообщение.

Одно и то же сообщение может одновременно увеличить длину нескольких очередей, т. е. сообщение может войти в несколько блоков QUEUE перед тем, как войти в соответствующие блоки DEPART.

Значение текущей длины очереди хранится в СЧА Q$<имя очереди>.

Блок DEPART имеет следующий формат:

DEPART A,[B]

Блок DEPART служит для уменьшения длины очереди.

В поле А задается номер или имя очереди, длину которой нужно уменьшить. В поле В задается число единиц, на которое уменьшается длина очереди. Это число не должно превышать текущую длину очереди. Если поле В пусто, длина очереди уменьшается на единицу.

Задания для самостоятельной работы:

- Увеличьте (уменьшите) на три единицы длину очереди с номером 3;

- Обнулите длину очереди QPR.

В результате выполнения программы моделирования работы вычислительной системы GPSS выдаст отчет:

GPSS World Simulation Report - proba31.2.1

Wednesday, January 19, 2000 20:42:57

START TIME END TIME BLOCKS FACILITIES STORAGES

0.1 0

NAME VALUE

B 10001.000

BR 10000.000

LABEL LOC BLOCK TYPE ENTRY COUNT CURRENT COUNT RETRY

1 GENERATE

2 QUEUE

3 SEIZE

4 DEPART

5 ADVANCE

6 RELEASE

7 TERMINATE

FACILITY ENTRIES UTIL. AVE. TIME AVAIL. OWNER PEND INTER RETRY DELAY

B

QUEUE MAX CONT. ENTRY ENTRY(0) AVE. CONT. AVE. TIME AVE.(-0) RETRY

BR357.472 0

CEC XN PRI M1 ASSEM CURRENT NEXT PARAMETER VALUE

FEC XN PRI BDT ASSEM CURRENT NEXT PARAMETER VALUE

Основные обозначения:

START TIME – время начала моделирования

END TIME - время окончания моделирования

BLOCKS - количество блоков, используемых в программе

FACILITIES – количество устройств

STORAGES – количество многоканальных устройств, для которых определяется емкость накопителя

Далее приводится информация о блоках:

LOC – номер блока, назначенный системой

BLOCK TYPE – название блока

ENTRY COUNT – количество транзактов, прошедших через блок за время моделирования

СURRENT COUNT – количество транзактов, задержанных в блоке на момент конца моделирования

RETRY – количество транзактов, ожидающих специальных условий для прохождения через данный блок

Отчет о работе устройства

FACILITY – название устройства

ENTRIES – количество транзактов, прошедших через устройство

UTIL. – вероятность загрузки устройства (часть периода моделирования, когда устройство было свободно)

AVE. TIME – среднее время обработки одного транзакта устройством

AVAIL. – состояние готовности устройства на момент конца моделирования (1 –готово к обслуживанию очередной заявки; 0 – не готово)

OWNER – номер последнего транзакта занимающего устройство (если не занималось, то значение 0)

PEND – количество транзактов, ожидающих устройство, и находящихся в режиме прерывания

INTER – количество транзактов, прерывающих устройство в данный момент

RETRY – количество транзактов, ожидающих специальных условий, зависящих от состояния объекта типа «устройство»

DELAY – определяет количество транзактов, ожидающих занятия или освобождения устройства

Статистика об очередях:

QUEUE – имя очереди

MAX - максимальная длина очереди

CONT. – текущая длина очереди

ENTRY – общее количество входов

ENTRY(0)- количество «нулевых» входов

AVE. CONT. – средняя длина очереди

AVE. TIME – среднее время пребывания транзактов в очереди

AVE.(-0) – среднее время пребывания в очереди без учета «нулевых» входов

RETRY – количество транзактов, ожидающих специальных условий

Информация о списке текущих событий

CEC (Current Events Chain)

XN – номер транзакта

PRI – приоритет транзакта (по умолчанию - 0)

M1 – время пребывания транзакта в системе с момента начал моделирования

ASSEM - номер семейства транзактов

CURRENT – номер блока в котором находится транзакт

NEXT – номер блока в который перейдет транзакт далее

PARAMETER – номер или имя параметра транзакта

VALUE – значение параметра

Информация о списке будущих событий

FEC (Future Events Chain)

XN – номер транзакта

PRI – приоритет транзакта

BDT - таблица модельных событий – абсолютное модельное время выхода транзакта из списка будущих событий (и перехода транзакта в список текущих событий)

ASSEM - номер семейства транзактов

CURRENT - номер блока в котором находится транзакт (0 – если транзакт не вошел в модель)

NEXT - номер блока в который перейдет транзакт далее

PARAMETER – номер или имя параметра транзакта

VALUE – значение параметра

Задача. Изменим условие задачи. Пусть в вычислительной системе два компьютера (интенсивность обработки заданий одинаковая), все остальные условия остаются без изменений.

В среде GPSS программа, моделирующая работу вычислительной системы, выглядит следующим образом:

NAK STORAGE 2

GENERATE 360,300

QUEUE BR

ENTER NAK

DEPART BR

ADVANCE 600,540

LEAVE NAK

TERMINATE 1

START 100

Обратите внимание, в программе появилась дополнительная строка NAK STORAGE 2.

И блоки SEIZE – RELEASE заменены соответственно на блоки ENTER –LEAVE, моделирующие работу с многоканальным устройством.

Рассмотрим подробнее работу этих блоков.

5. Моделирование многоканальных устройств

Устройство в GPSS используют для моделирования одиночного устройства обслуживания. Два или более обслуживающих устройств, работающих параллельно, могут моделироваться двумя или более одинаковыми устройствами. Это необходимо, когда устройства являются разнородными.

Если параллельно работающие устройства являются одинаковыми, то для их моделирования может использоваться объект многоканальное устройство (МКУ).

Количество устройств, которое моделирует МКУ задает пользователь с помощью оператора STORAGE

Формат оператора:

Метка STORAGE А

Метка – имя МКУ

А – емкость МКУ (количество однотипных устройств, входящих в МКУ)

Блок ENTER имеет следующий формат записи:

ENTER A,[B]

Блок ENTER позволяет вошедшему сообщению (транзакту) использовать много­канальное устройство. Сообщение может быть задержано на входе в блок, если многоканальное устройство заполнено или имеющейся емкос­ти недостаточно или устройство в данный момент недоступно.

В поле А указывается номер или имя многоканального устройст­ва, куда входит сообщение.

В поле В содержится число занимаемых единиц многоканального устройства. Если поле В пусто, то предполагается что занимается од­на единица. Если это значение равно нулю, то сообщение никогда не задерживается на входе, а блок рассматривается как нерабочий.

Активное сообщение не может войти в блок ENTER, если запрос на многоканальное устройство не может быть удовлетворен.

Активное сообщение не может войти в блок ENTER, если многока­нальное устройство находится в недоступном состоянии.

Когда сообщение входит в блок ENTER, то операнд А использует­ся для нахождения многоканального устройства с указанным именем. Если такое многоканальное устройство не существует, то возникает ошибка выполнения. В противном случае используется операнд В для оценки емкости многоканального устройства.

Одно и то же сообщение может входить в неограниченное число многоканальных устройств, а впоследствии освобождать их (или часть из них).

Блок LEAVE имеет следующий формат:

LEAVE A,[B]

Блок LEAVE освобождает определенное число единиц многоканаль­ного устройства. Занятый объем многоканального устройства уменьшается на число освобождаемых единиц. Оставшаяся емкость многоканального устройства увеличивается на ту же величину. Счетчик числа входов не изменяет­ся.

Поле А блока LEAVE определяет номер или имя многокального ус­тройства.

Поле В - число освобождаемых единиц многоканального устройст­ва. Если это поле пусто, предполагается 1. Число осво­бождаемых единиц не должно превышать текущее содержимое многоканального устройства.

Задания для самостоятельной работы:

- Морские суда прибывают в порт каждые 15-25 часов. В порту имеется 10 причалов. Каждый корабль по длине занимает 3 причала и находится в порту 7-13 часов. Промоделируйте работу порта на протяжении 500 часов. Напишите сегмент GPSS программы.

В результате выполнения программы моделирования работы вычислительной системы с двумя компьютерами GPSS выдаст отчет с информацией об использовании МКУ:

STORAGE – имя МКУ

CAP. – емкость МКУ, заданную оператором STORAGE

REM. – количество единиц свободной емкости в конце периода моделирования

MIN. – минимальное количество емкости за используемый период

MAX. - максимальное количество емкости за используемый период

ENTRIES – количество входов в МКУ за период моделирования

AVL. – состояние готовности МКУ в конце периода моделирования (1 – МКУ готов, 0 – нет)

AVE. C. – среднее значение занятой емкости за период моделирования

UTIL. – средний коэффициент использования всех устройств МКУ

RETRY – количество транзактов, ожидающих специальных условий, зависящих от состояния МКУ

DELAY – определяет количество транзактов, ожидающих занятия или освобождения устройства МКУ

Задание. Сравните отчеты по результатам моделирования работы вычислительной системы с одним компьютером и с двумя. Какие показатели изменились и как? Какой вариант организации работы вычислительной системы более предпочтителен?

11.4. Моделирование значений случайной величины с заданным законом распределения и обработка результатов моделирования средствами GPSS/World

1. Моделирование последовательности значений случайных величин с заданным законом распределения

Моделирование последовательности значений случайных величин с заданным законом распределения реализуется на основе использования случайных величин, имеющих равномерное распределение в интервале (0, 1) [3, 5, 6].

Для получения случайной величины Y с равномерным распределением на интервале (0;1) в GPSS имеются встроенные генераторы случайных чисел. Для получения случайного числа путем обращения к такому генератору достаточно записать RN с номером генератора, например RN1. Правда, встроенные генераторы случайных чисел GPSS/World дают числа не на интервале (0;1), а целые случайные числа, равномерно распределенные от 0 до 999, но их нетрудно привести к указанному отрезку делением на 1000.

При каждом запуске системы генераторы выдают одну и ту же последовательность чисел. Команда PMULT позволяет изменить эту последовательность путем изменения начальных множителей.

Формат команды: PMULT A,B,C,D,E,F,G

Операнды A,B,C,D,E,F,G задают соответственно начальные множители для 1-7 генераторов случайных чисел.

Например, PMULT 890,,,5, устанавливает начальные состояния множителей генераторов случайных чисел 1 и 4.

Вычисления в GPSS выполняются с использованием переменных. Они могут быть целыми и действительными (с плавающей точкой). Действительные переменные определяются перед началом моделирования с помощью оператора определения FVARIABLE (переменная), имеющего следующий формат:

Имя FVARIABLE выражение

Здесь имя - имя переменной, используемое для ссылок на нее, а выражение - арифметическое выражение, определяющее переменную.

Арифметическое выражение представляет собой комбинацию операндов, в качестве которых могут выступать константы, функции, знаки арифметических операций и круглых скобок. Следует заметить, что знаком операции умножения в GPSS является символ #.

Переменные могут быть использованы для получения значений случайной величины с заданным законом распределения. Пусть необходимо сгенерировать 100 значений равномерно распределенной СВ на интервале [5, 15].

TARR FVARIABLE 10#(RN1/1000)+5

GENERATE V$TARR

TERMINATE 1

START 100

Для получения значений случайной величины Y с показательным (экспоненциальным) законом необходимо воспользоваться соотношением 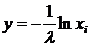, полученным на основе метода обратной функции (см. раздел 7.2. в учебном пособии). Для имеем:

TARR1 FVARIABLE (-1)#LOG(RN1/1000)

GENERATE V$TARR1

TERMINATE 1

START 100

Такой способ является достаточно трудоемким, так как требует обращения к математическим функциям, вычисление которых требует десятков машинных операций. Другим возможным способом является использование вычислительных объектов GPSS типа функция.

Функции используются для вычисления величин, заданных табличными зависимостями. Каждая функция определяется перед началом моделирования с помощью оператора определения FUNCTION (функция), имеющего следующий формат:

Имя FUNCTION A,B

Здесь имя - имя функции, используемое для ссылок на нее; A – стандартный числовой атрибут, являющийся аргументом функции; B - тип функции и число точек таблицы, определяющей функцию.

Существует пять типов функций. Непрерывные числовые функции, тип которых кодируется буквой C. Так, например, в определении непрерывной числовой функции, таблица которой содержит 24 точки, поле B должно иметь значение C24.

При использовании непрерывной функции для генерирования случайных чисел ее аргументом должен быть один из генераторов случайных чисел RNj. Так, оператор для определения функции показательного распределения может иметь следующий вид:

EXP FUNCTION RN1,C24

Особенностью использования встроенных генераторов случайных чисел RNj в качестве аргументов функций является то, что их значения в этом контексте интерпретируются как дробные числа от 0 до 0,999999.

Таблица с координатами точек функции располагается в строках, следующих непосредственно за оператором FUNCTION. Эти строки не должны иметь поля нумерации. Каждая точка таблицы задается парой Xi (значение аргумента) и Yi (значение функции), отделяемых друг от друга запятой. Пары координат отделяются друг от друга символом "/" и располагаются на произвольном количестве строк. Последовательность значений аргумента Xi должна быть строго возрастающей.

Как уже отмечалось, при использовании функции в поле B блоков GENERATE и ADVANCE вычисление интервала поступления или времени задержки производится путем умножения операнда A на вычисленное значение функции. Отсюда следует, что функция, используемая для генерирования случайных чисел с показательным (экспоненциальным) распределением , должна описывать зависимость y=-ln(1-x) (данная зависимость получена на основе использования метода обратной функции, см. раздел 7.2. в учебном пособиичена на основе исползсел 1,л. ельность путем изменения начальных мнежителей.

л. ()), представленную в табличном виде.

Оператор FUNCTION с такой таблицей, содержащей 24 точки для обеспечения достаточной точности аппроксимации, имеет следующий вид:

EXP FUNCTION RN1,C24

0,0/.1,.104/.2,.222/.3,.355/.4,.509/.5,.69/.6,.915

.7,1.2/.75,1.38/.8,1.6/.84,1.85/.88,2.12/.9,2.3

.92,2.52/.94,2.81/.95,2.99/.96,3.2/.97,3.5/.98,3.9

.99,4.6/.995,5.3/.998,6.2/.999,7/.9998,8

Вычисление непрерывной функции производится следующим образом.

Сначала определяется интервал (Xi;Xi+1), на котором находится текущее значение СЧА-аргумента (в нашем примере - сгенерированное значение RN1). Затем на этом интервале выполняется линейная интерполяция с использованием соответствующих значений Yi и Yi+1. Результат интерполяции используется в качестве значения функции. Если функция служит операндом B блоков GENERATE или ADVANCE, то результат умножается на значение операнда A.

Использование функций для получения случайных чисел с заданным распределением дает хотя и менее точный результат за счет погрешностей аппроксимации, но зато с меньшими вычислительными затратами (несколько машинных операций на выполнение линейной интерполяции). По сути, этот вариант реализации (получения последовательности значений СВ) соответствует методу кусочной аппроксимации функции плотности распределения вероятностей (см. раздел 7.2 учебного пособия).

Функции всех типов имеют единственный системный числовой атрибут с названием FN, значением которого является вычисленное значение функции. Вычисление функции производится при входе транзакта в блок, содержащий ссылку на СЧА FN с именем функции.

При большом количестве транзактов, пропускаемых через модель (десятки и сотни тысяч), разница в скорости вычислений по данному способу и способу, описанному выше, должна стать заметной.

EXP1 FUNCTION RN1,C24

0,0/.1,.104/.2,.222/.3,.355/.4,.509/.5,.69/.6,.915

.7,1.2/.75,1.38/.8,1.6/.84,1.85/.88,2.12/.9,2.3

.92,2.52/.94,2.81/.95,2.99/.96,3.2/.97,3.5/.98,3.9

.99,4.6/.995,5.3/.998,6.2/.999,7/.9998,8

GENERATE 100,FN$EXP1

TERMINATE 1

START 100

В примере среднее значение СВ равно 100.

Пример табличного задания нормального распределения СВ, используется 25 точки для обеспечения достаточной точности аппроксимации.

NOR1 FUNCTION RN1, C25

0,-5/.00003,-4/.00135,-3/.00621,-2.5/.02275,-2

.06681,-1.5/.11507,-1.2/.15866,-1/.21186,-.8/.27425,-.6

.34458,-.4/.42074,-.2/.5,0/.57926,.2/.65542,.4

.72575,.6/.78814,.8/.84134,1/.88493,1.2/.93319,1.5

.97725,2/.99379,2.5/.99865,3/.99997,4/1,5

Данная таблица задает СВ Z с математическим ожиданием равным 0, и СКО равным 1. Для моделирования нормальной СВ X с другими значениями математического ожидания и СКО необходимо произвести вычисления по формуле:

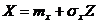
Если математическое ожидание =5; среднеквадратическое отклонение =2, то

GENERATE (5+2#FN$NOR1)

TERMINATE 1

START 100

2. Обработка результатов моделирования

Для получения оценок математического ожидания (среднего значения) и дисперсии последовательности значений СВ, полученных в GPSS необходимо использовать блоки сбора статистики TABLE и TABULATE.

Оператор описания таблицы TABLE имеет следующий формат:

<NAME> TABLE <A>,<B>,<C>,<D>

Оператор определяет аргумент, а также число и ширину частотных интервалов.

Метка NAME определяет имя таблицы.

В поле А задается аргумент таблицы - элемент данных, чье частотное распределение будет табулироваться. Операнд может быть именем, целым, СЧА или СЧА*<параметр>.

В поле В задается верхний предел первого интервала. Операнд может целым или именем.

В поле С задается ширина частотного интервала - разница между верхней и нижней границей каждого частотного класса. Операнд может быть положительным целым.

В поле D задается число частотных интервалов. Это число не может превышать 8191. Операнд может быть положительным целым.

Для сбора элементов данных сообщение должно войти в блок TABULATE с тем же именем таблицы, что определено в блоке TABLE.

Когда сообщение входит в блок TABULATE, оценивается аргумент таблицы (операнд А в операторе TABLE). Если он меньше или равен операнду В в операторе TABLE, то выбирается первый частотный класс таблицы. Если аргумент таблицы не подходит для этого класса, то класс выбирается путем деления значения аргумента на операнд С оператора TABLE. Нижняя граница частотного класса включается в предыдущий класс. Если таблицы не достаточно для размещения этого значения, то выбирается последний частотный интервал. Затем выбирается целое из частотного класса и счетчик увеличивается на величину, определяемую операндом В оператора TABULATE. По умолчанию увеличение происходит на 1. В конце работы оператора TABULATE изменяются значения среднего и стандартного отклонения аргумента таблицы.

Таблица может быть переопределена или переинициализирована другим оператором TABLE, с той же самой меткой, что и первая.

Стандартные числовые атрибуты, связанные с описываемым опера-

тором, следующие:

- ТВ - среднее значение аргумента;

- ТС - число входов в таблицу;

- ТD - стандартное отклонение.

Блок, связанный с оператором TABLE - TABULATE.

Блок TABULATE имеет следующий формат:

TABULATE <А>,[<B>]

Блок TABULATE табулирует текущее значение заданного аргумента. Способ табуляции зависит от режима работы таблицы, который определяется оператором описания таблицы TABLE.

В поле А задается номер или имя таблицы, в которую табулируется значение аргумента. Таблица должна быть определена оператором описания TABLE.

В поле В задается число единиц, которые должны быть занесены в тот частотный интервал, куда попало значение аргумента. Если поле В пусто, эта величина полагается равной единице.

Когда сообщение входит в блок TABULATE, то для нахождения таблицы используется операнд А. Если такой таблицы нет, то возникает ошибка выполнения. Таблица должна быть определена оператором TABLE. Таблица изменяется в соответствии с операндами оператора TABLE.

Пример использования блоков TABLE и TABULATE.

TT TABLE M1,40,50,8

EXP1 FUNCTION RN1,C24

0,0/.1,.104/.2,.222/.3,.355/.4,.509/.5,.69/.6,.915

.7,1.2/.75,1.38/.8,1.6/.84,1.85/.88,2.12/.9,2.3

.92,2.52/.94,2.81/.95,2.99/.96,3.2/.97,3.5/.98,3.9

.99,4.6/.995,5.3/.998,6.2/.999,7/.9998,8

GENERATE 100,FN$EXP1

ADVANCE 100,FN$EXP1

TABULATE TT

TERMINATE 1

START 100

Здесь М1 – константа (стандартный числовой атрибут), которая связана с каждым транзактом и хранит время пребывания транзакта в модели. Время пребывания транзакта в модели определяется блоком ADVANCE и распределено по показательному закону с =1/100. Строится частотное распределение, вычисляются оценки математического ожидания и среднеквадратического отклонения для М1, т. е. для времени пребывания транзакта в модели. Граница первого интервала задана 40; ширина интервала группирования – 50; число интервалов группирования – 8. Все эти параметры задаются опытным путем.

Ниже приведен фрагмент отчета, выдаваемый GPSS по результатам работы программы.

TABLE MEAN STD. DEV. RANGE RETRY FREQUENCY CUM.%

TT 101.

_ - 40.

40.61.00

90.70.00

140.78.00

190. 88.00

240.94.00

290.99.00

340.000 - _ 1 100.00

Mean – это среднее значение или оценка математического ожидания;

STD. DEV – это оценка среднеквадратического отклонения;

Range – интервалы группирования;

FREQUENCY – количество наблюдений, попавших в каждый интервал.

Таким образом, погрешность в оценке математического ожидания составила:

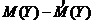==100-101.032=-1.032

Погрешность в оценке среднеквадратического отклонения составила:

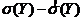==100-101.889=-1.889.

Таким образом, точность имитационного моделирования значений СВ по методу кусочной аппроксимации функции плотности распределения вероятностей в среде GPSS достаточно высокая.

Для построения гистограммы необходимо выбрать после выполнения программы пункт меню Window/Simulation Window/Table Window. Далее в открывшемся диалоговом окне задать имя таблицы (в данном примере TT). Вид гистограммы приведен на рис. 1.

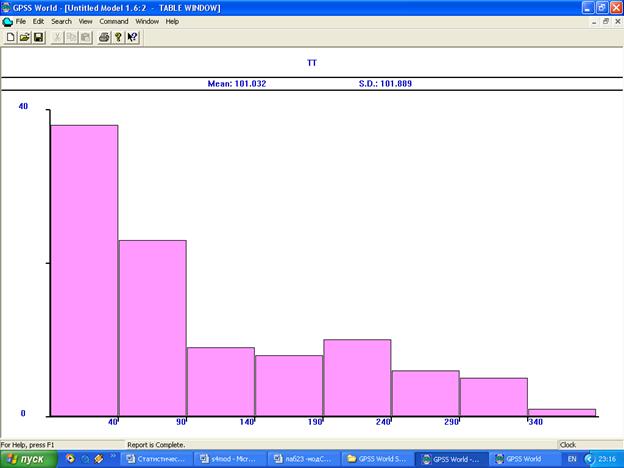Рис. 15.Гистограмма значений СВ Y

Визуальный анализ гистограммы позволяет сделать вывод о согласии выборочных значений СВ Y с моделью экспоненциального распределения.

11.5. Основные направления развития инструментальных средств моделирования

Языки имитационного моделирования позволяют за сравнительно короткий срок составлять программные модели довольно сложных систем. К сожалению, такие модели обладают низкой способностью отвечать на вопросы типа "а что, если...", поскольку это именно те вопросы, которые наиболее полезны, так как они способствуют более глубокому пониманию проблемы и поиску лучших способов оценки возможных действий. Для ответа на подобные вопросы часто приходится непосредственно изменять программный код модели, что повышает затраты времени на анализ системы. При использовании языков имитационного моделирования возникает также другая проблема: затраты на изучение и освоение языка, тем более, что эти языки оперируют абстрактными понятиями, в то время как экспериментатор часто является специалистом в той области, которой принадлежит моделируемая система, и применяет специфическую терминологию, что может значительно осложнить освоение языка исследователем.

В настоящее время языки имитационного моделирования получили дальнейшее развитие в виде визуальных средств моделирования, где исследователь оперирует не командами и операторами языка, а объектами, представляемыми в графическом виде. Примером такой системы может служить ARENA. Визуальные средства моделирования частично снимают проблемы языков имитационного моделирования, описанные чуть выше, но в то же время основные из них остаются, например, освоение исследователем абстрактных терминов, используемых в этих средствах.

Вторым направлением развития инструментальных средств имитационного моделирования являются узкоспециализированные моделирующие программные комплексы. Преимуществами таких комплексов является быстрая реализация модели, использование терминологии, понятной исследователю, применяющему это средство, позволяют быстро отвечать на вопросы типа "а что, если...".

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5