Для ординарного потока можно пренебречь возможностью совместного появления на элементарном участке двух и более событий. В каждый момент времени в СМО может поступать не более одной заявки
отсутствие последействия - для любых не перекрывающихся участков времени T1,T2,…,Tn числа событий Х1=Х(t1,T1),Х2=Х(t2,T2),…., Хn = Х(tn, Tn), попадающих на эти участки, представляют собой независимые случайные величины, т. е. вероятность попадания любого числа событий на один из участков не зависит от того, сколько их попало на другие.
Отсутствие последействия означает, что для любого момента времени t0, будущие моменты наступления события потока (при t>t0) не зависят от того, в какие моменты наступали события в прошлом (при t<t0).
Ординарный поток событий, в котором отсутствует последействие, называется пуассоновским потоком.
стационарность
Поток событий называется стационарным, если все его вероятностные характеристики не меняются со временем. В частности, для стационарного потока событий вероятность попадания того или иного числа событий на участок длины T
зависит только от длины этого участка и не зависит от того, где именно на оси времени 0t этот участок расположен.
Это значит, что числа событий Х1(t1, T) и Х2(t2, T), попадающих на два участка одинаковой длины T, будут иметь одинаковые распределения. Отсюда следует, в частности, что для стационарного потока событий его интенсивность l(t) постоянна:
l(t) = l = const
Поток событий, обладающий всеми тремя свойствами, называется простейшим (или стационарным пуассоновским потоком).
Кроме того, к достоинствам простейшего потока можно также отнести следующее:
а) Сумма N независимых, ординарных и стационарных потоков заявок с интенсивностями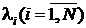 
сходится к простейшему потоку с интенсивностью 
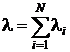, при условии, что складываемые потоки оказывают более или менее одинаково малое влияние на суммарный поток;
б) Поток заявок, полученный путем случайного разрежения
исходного потока, когда каждая заявка с определенной
вероятностью p исключается из потока независимо от того, исключены другие заявки или нет, образует простейший поток с интенсивностью 
, где 
- интенсивность исходного потока. В отношении исходного потока заявок делается предположение лишь об ординарности и стационарности.
Поток с ограниченным последействием (рекуррентный поток) – поток, у которого случайные интервалы t1, t2,…, tn между соседними по времени событиями представляют собой независимые случайные величины. При его моделировании применяется последовательная (рекуррентная процедура): сначала разыгрывается величина t1, затем t2 и т. д. Например, последовательность вызовов такси.
Поток без последействия является частным случаем потока с ограниченным последействием.
Поток Пальма. Стационарный поток с ограниченным последействием называется потоком Пальма. Для такого потока интервалы t1, t2,…, tn между соседними событиями представляют собой последовательность независимых, одинаково распределенных СВ.
Простейший пуассоновский поток является потоком Пальма. У простейшего потока интервалы t1, t2,…, tn распределены одинаково, по показательному закону и независимы между собой. Поток Пальма отличный от простейшего получается, если интервалы между событиями распределены по другому закону.
Потоки Эрланга, их свойства и применение.
Потоком Эрланга k-го порядка называется поток Пальма, у которого интервалы времени между событиями распределены по закону Эрланга k-го порядка. Поток Эрланга k-го порядка может быть получен из простейшего с помощью его прореживания. В простейшем потоке сохраняется каждое k-е событие, остальные отбрасываются. Привести схему формирования:
Интервал между соседними событиями в потоке Эрланга 3-го порядка – сумма трех независимых СВ, имеющих показательное распределение с параметром 
.
.
Поток Эрланга k-го порядка
.
Функция плотности распределения интервала времени между двумя событиями 
для СВ 
имеет вид:
- закон Эрланга k-го порядка.
Числовые характеристики СВ :
Математическое ожидание длины интервала времени между последовательными моментами поступления событий:
Дисперсия интервала времени между последовательными моментами поступления событий:
.
Свойства потока Эрланга.
При k=1 получается обычное экспоненциальное распределение, а при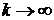 
поток Эрланга приближается к регулярному потоку с постоянным интервалом между событиями (M). Это свойство потоков Эрланга удобно в практических применениях: оно дает возможность, задаваясь различными k, получать потоки, обладающие различным последействием - от полного отсутствия последействия (к=1), до жесткой функциональной связи между моментами появления событий (
).
+ все свойства простейшего потока: стационарность, ординарность.
9.2. Марковский случайный процесс
Второе понятие, которое часто используют при моделировании систем – это понятие случайного процесса.
Пусть имеется некоторая система S, которая в процессе функционирования может принимать различные состояния Si, i=1..n. Если состояния системы меняются случайным образом, то последовательность состояний системы образует случайный процесс.
Различают системы с непрерывным и дискретным временем.
Системы с непрерывным временем предполагают, что переход системы из одного состояния в другое может осуществляться в любой момент времени, т. е. время пребывания системы в каждом состоянии представляет непрерывную случайную величину.
Для систем с дискретным временем время пребывания системы в каждом состоянии фиксированное, а моменты переходов t1, t2, ..., tk размещаются на временной оси через равные промежутки и называются "шагами" или "этапами". Время нахождения системы в некотором состоянии представляет дискретную случайную величину.
Полное множество состояний Si исследуемой системы может быть либо конечным (i = 1, n), либо бесконечно большим. Большинство реальных систем имеют дискретное конечное пространство состояний. Последовательность состояний такой системы Si (i = 1, n) и сам процесс переходов из состояния в состояние называется цепью.
Дискретные цепи Маркова
Пусть имеется система S с дискретными состояниями s1, s2, …, sn.
Процесс, протекающий в системе S, называется Марковским процессом с дискретными состояниями и дискретным временем (или дискретной Марковской цепью), если выполняется условие: для любого фиксированного момента времени (любого шага) условные вероятности состояния системы в будущем зависят только от состояния системы в настоящем и не зависят от того, когда (на каком шаге) и откуда система перешла в это состояние.
Например, рассматривается процесс: система представляет техническое устройство, которое осматривается в определенные моменты времени (например, через сутки) и ее состояние регистрируется. Каждый осмотр – шаг процесса. Возможные состояния следующие:
s1 – полностью исправно;
s2 – частично исправно, необходима наладка;
s3 – серьезная неисправность, требует ремонта;
s4 – непригодно.
Основной задачей исследования Марковской цепи является нахождение безусловных вероятностей нахождения системы S на любом шаге k в состоянии si.
Непрерывные цепи Маркова
На практике Марковские процессы с дискретным состоянием и дискретным временем встречаются довольно редко. Как правило, рассматривают Марковские случайные процессы с дискретными состояниями и непрерывным временем.
Пусть имеется некоторая система S, переходы системы из состояния в состояние происходят в случайные моменты времени. Переходы системы из состояния в состояние происходят под воздействием каких-либо потоков событий (например, «поток отказов», поток восстановлений).
Для системы такими событиями могут быть:
- поступление очередной заявки в СМО (систему массового обслуживания) (событие входного потока);
- окончание обслуживания очередной заявке (событие потока обслуживании заявок), и т. д.
Процесс, протекающий в системе S, называется Марковским процессом с дискретными состояниями и непрерывным временем (или непрерывной Марковской цепью), если выполняется условие: для любого фиксированного момента времени условные вероятности состояния системы в будущем зависят только от состояния системы в настоящем и не зависят от того, когда (на каком шаге) и откуда система перешла в это состояние.
Схематично СМО удобно представлять в виде размеченного графа состояний
Пусть 
- совокупность возможных состояний системы.
Например, рассматриваемая система – компьютер, обрабатывающий поток заданий. В очереди на обработку может стоять не более двух заданий. Поток заданий Пуассоновский с интенсивностью , поток обслуживания Пуассовноский с интенсивностью 
.
- в системе нет ни одной заявки, компьютер простаивают;
- в системе одна заявка, компьютер работает;
- в системе 2 заявки, компьютер работают и одна заявка в очереди;
- в системе 3 заявки, компьютер работают и две заявки в очереди
Граф состояний – схема, отражающая переход системы из состояния в состояние.
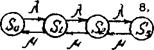
Вершины графа соответствуют состояниям, дуги – переходам из состояния в состояние.
Размеченный граф состояний - граф состояний с проставленными у стрелок интенсивностями соответствующих потоков событий, переводящих систему из состояния в состояние.
Здесь и в дальнейшем предполагается ординарность суммарного потока всех событий в СМО, то есть одновременно не могут произойти два и более событий. В данной СМО одновременно невозможно окончание обслуживание и поступление на вход СМО заявки. Другим предположением является нулевое время перехода заявки из очереди на канал обслуживания и момент его освобождения.
Можно доказать, что если все потоки событий, переводящие систему из состояния в состояние пуассоновские и независимые, то процесс, протекающий в системе – Марковский.
Обозначим 
- вероятность того, что в момент t система будет находиться в состоянии 
(
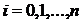). Очевидно, для любого момента t сумма вероятностей состояний равна единице:
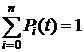
так как события, состоящие в том, что в момент t система S находится состояниях 
, которые несовместны и образуют полную группу.
Оказывается, зная размеченный граф состояний, можно определить вероятности состояний как функцию времени. А именно, эти вероятности удовлетворяют определенного вида дифференциальным уравнениям, называемым уравнениями Колмогорова. Решая эти уравнения, мы получим искомые вероятности.
Общее правило составления дифференциальных уравнений, справедливое для любой непрерывной марковской цепи.
В левой части каждого уравнения стоит производная вероятности состояния, а правая часть содержит столько членов, сколько стрелок связано с данным состоянием. Если стрелка направлена из состояния, то соответствующий член имеет знак «минус»; если стрелка направлена в состояние - знак «плюс». Каждый член равен произведению интенсивности потока событий, соответствующего данной стрелке, умноженной на вероятность того состояния, из которого исходит стрелка.
Для примера, рассмотренного выше, система уравнений Колмогорова будет иметь вид:
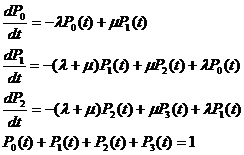
Уравнение для последнего состояния (или одного из состояний) не составляется, а заменяется нормировочным условием.
Стационарный режим для непрерывной цепи Маркова
Известно, что все потоки событий - простейшие (стационарные пуассоновские) потоки. Поставим теперь следующий вопрос: что будет происходить с системой S при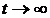 
? Будут ли функции стремиться к каким-то пределам? Эти пределы, если они существуют, называются предельными вероятностями состояний.
Можно доказать следующее общее положение. Если число состояний системы S конечно и из каждого состояния можно перейти (за то или иное число шагов) в каждое другое, то предельные вероятности состояний существуют и не зависят от начального состояния системы.
Таким образом, если поставленное условие выполнено, то при в системе устанавливается некоторый предельный стационарный режим. Он состоит в том, что система случайным образом меняет свои состояния, но вероятность каждого из них уже не зависит от времени: каждое из состояний осуществляется с некоторой постоянной вероятностью. Эта вероятность представляет собой не что иное, как среднее относительное время пребывания системы в данном состоянии. Например, если у системы S три возможных состояния: 
, причем их предельные вероятности равны 0.2, 0.3,0.5, то это означает, что после перехода к установившемуся режиму система S в среднем две десятых времени будет находиться в состоянии 
, три десятых - в состоянии
, половину времени - в состоянии 
.
Для вычисления предельных вероятностей необходимо в системе уравнений Колмогорова положить все левые части (производные) равными нулю. Действительно, в предельном (установившемся) режиме все вероятности состояний постоянны, значит, их производные равны нулю.
Следовательно, система дифференциальных уравнений превращается в систему линейных алгебраических уравнений, точнее, в систему однородных уравнений (без свободных членов). Для получения решения требуется одно из уравнений системы заменить на нормировочное уравнение 
Для примера, рассмотренного выше:
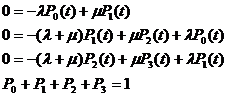
9.3. Марковский случайный процесс «гибели и размножения»
В приведенном выше примере состояния системы образуют цепь, каждое состояние, кроме исходного и последнего, связано прямой и обратной связью с двумя соседними состояниями. Крайние состояния связаны с одним соседним. Такая схема процесса, протекающего в системе, называется схемой «Гибели и размножения», а сам процесс называют процессом «гибели и размножения».
Если в такой системе все потоки, переводящие систему из состояния в состояние Пуассоновские, то процесс называется Марковским случайным процессом «гибели и размножения».
Термин ведет начало от биологических задач, процесс описывает изменение численности популяции. Переход из состояния в состояние происходит в момент гибели или рождения особи.
На практике значительная часть систем может описываться в рамках процесса «гибели и размножения».
10. Элементы теории массового обслуживания, применяемые при моделировании систем
10.1. Основные определения и понятия. Структура СМО. Классификация СМО
Под системой массового обслуживания (СМО) понимают динамическую систему, предназначенную для эффективного обслуживания потока заявок (требований на обслуживание) при ограничениях на ресурсы системы.
Первые задачи теории систем массового обслуживания (ТСМО) были рассмотрены сотрудниками Копенгагенской телефонной компании, датским ученым (1878г. – 1929г.) в период между 1908 и 1922гг. Эти задачи были вызваны к жизни стремлением упорядочить работу телефонной сети и разработать методы, позволяющие заранее повысить качество обслуживания потребителей в зависимости от числа используемых устройств. Оказалось, что ситуации, возникающие на телефонных станциях, являются типичными не только для телефонной связи. Работа аэродромов, работа морских и речных портов, магазинов, терминальных классов, радиолокационных комплексов, радиолокационных станций и т. д. и т. д. может быть описана в рамках ТСМО.
Приведем примеры систем массового обслуживания.
Пример 1. Телефонная связь времен Эрланга представляла собой телефонную станцию, связанную с большим числом абонентов. Телефонистки станции по мере поступления вызовов соединяли телефонные номера между собой.
Задача: Какое количество телефонисток (при условии их полной занятости) должно работать на станциях для того, чтобы потери требований были минимальны.
Пример 2. Система скорой помощи некоего городского района представляет собой пункт, который принимает на выполнение некоторое количество автомашин скорой помощи и несколько врачебных бригад.
Задача: Определить количество врачей, вспомогательного персонала, автомашин, для того, чтобы время ожидания вызова было для больных оптимальным при условии минимизации затрат на эксплуатацию системы и максимизации качества обслуживания.
Пример 3. Важной задачей является организация морских и речных перевозок грузов. При этом особое значение имеют оптимальное использование судов и портовых сооружений.
Задача: Обеспечить определенный объем перевозок при минимальных расходах. При этом сохранить простои судов при погрузочно-разгрузочных работах.
Пример 4. Система обработки информации содержит мультиплексный канал и несколько компьютеров. Сигналы от датчиков поступают на мультиплексный канал, где буферизуются и предварительно обрабатываются. Затем поступают в тот компьютер, где очередь минимальна.
Задача: Обеспечить ускорение обработки сигналов при заданной суммарной длине очереди.
На рис. 13 изображена структурная схема типичной системы массового обслуживания – ремонтного предприятия.
Нетрудно привести множество других примеров из самых различных областей деятельности. Характерным для таких задач является:
- условие двойной случайности: случайный момент времени поступления заказа на обслуживание (на телефонную станцию, на пункт скорой помощи, на вход процессора, случайный момент времени прибытия морского судна на погрузку и т. д.); случайная длительность времени обслуживания;
- наличие очередей (судов перед шлюзами, машин перед туннелями, покупателей перед прилавками, задач на входе процессора вычислительного комплекса и т. д.).
Реальные системы, с которыми приходится иметь дело на практике, как правило, очень сложны и включают в себя ряд этапов (стадий) обслуживания (рис. 14). Причем на каждом этапе может существовать вероятность отказа в выполнении или существует ситуация приоритетного обслуживания по отношению к другим требованиям. При этом отдельные звенья обслуживания могут прекратить свою работу (для ремонта, подналадки и т. д.) или могут быть подключены дополнительные средства. Могут быть такие обстоятельства, когда требования, получившие отказ, вновь возвращаются в систему (подобное может происходить в информационных системах).
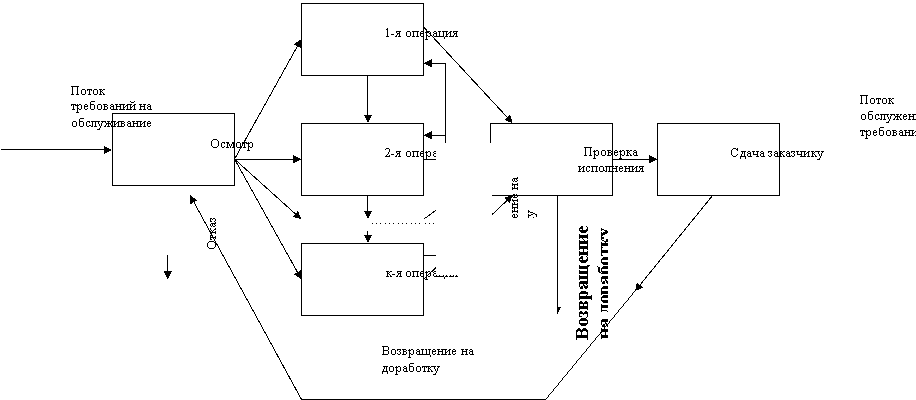
Рис. 13. Структурная схема типичной системы массового обслуживания – ремонтного предприятия
Структура СМО. Все СМО имеют вполне определенную структуру, изображенную на рис. 14.
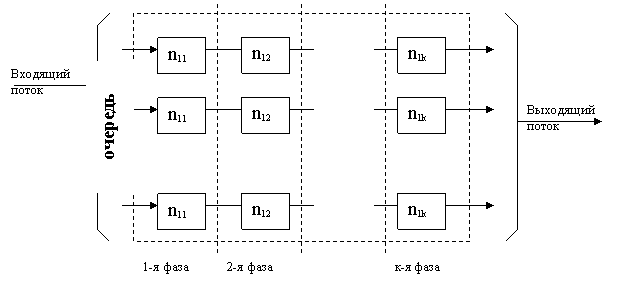
Рис. 14.
Основные определения ТСМО.
1. Потоком называют последовательность событий. Поток, состоящий из требований на обслуживание, назовем потоком требований.
2. Поток требований, поступающих в обслуживающую систему, назовем входным потоком.
3. Поток требований, которые обслужены, называется выходным потоком.
4. Совокупность очередей и приборов (каналов) обслуживания называется системой обслуживания.
5. Каждое требование поступает на свой канал, где подвергается операции обслуживания.
6. Каждая СМО имеет правила формирования очереди и правила или дисциплину обслуживания.
Классификация СМО.
Можно выделить различные признаки классификации СМО.
СМО делятся на системы с отказами и системы без отказов.
В системе с отказами (с потерями, с конечной длиной очереди) заявка, пришедшая в момент, когда все каналы обслуживания заняты или заняты все места в очереди, получает отказ и покидает систему.
В системе без отказов (без потерь, с бесконечной длиной очереди) такая заявка не покидает систему, а становится в очередь и ждет, пока не освободится какой-нибудь канал. Время ожидания в общем случае неограниченно. Неограниченным может быть и количество требований, поступающих в систему.
СМО делятся на замкнутые и разомкнутые.
В замкнутых СМО в системе циркулирует определенное конечное число заявок (конечное число требований).
В разомкнутых СМО количество, поступающих заявок бесконечно.
СМО делятся на многоканальные и одноканальные системы в зависимости от количества обслуживающих каналов.
В n-канальной CМО одновременно может обслуживаться n заявок. Каналы обслуживания иногда называют обслуживающими аппаратами (ОА).
В простейшем случае каждый ОА характеризуется своей производительностью (интенсивностью обслуживания заявок). Если в СМО поступают заявки нескольких типов, то для каждого типа заявок может быть задана соответствующая интенсивность обслуживания.
Длительность обслуживания заявки в ОА в общем виде - это случайная величина с законом распределения 
и математическим ожиданием (средним значением) M. Например, длительность обслуживания заявки процессором определяется временем выполнения соответствующей программы.
В случае малой разветвлённости программы, когда число выполняемых операций практически постоянно, длительность обслуживания может считаться постоянной и равной M. В общем случае прикладные программы реализуют сложные алгоритмы с большим числом разветвлений. Количество операций, выполняемых в процессе обслуживания заявок одного типа, зависит от того, по какой ветви идет реализация алгоритма. В свою очередь путь реализации алгоритма определяется состоянием управляемого объекта, т. е. данными, поступающими в управляющую систему. В этом случае время выполнения программы рассматривается как случайная величина с математическим ожиданием M, и дисперсией D.
Однако, если известно, что время обслуживания - случайная величина с известным значением её математического ожидания, а сведения о законе распределения отсутствует, то время выполнения программы целесообразно аппроксимировать экспоненциальным распределением
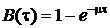
где, 
- интенсивность обслуживания (количество заявок, которое может быть обслужено в единицу времени.). Достоинства такой аппроксимации были перечислены ранее. Если в одноканальную CМO с интенсивностью обслуживания поступает входной поток заявок с интенсивностью , то величина 
называется загрузкой СМО, или по-другому, вероятностью
того, что в произвольный момент времени ОА работает (не
простаивает). Так как 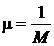, то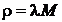 
По приоритету заявок:
- СМО с заявками, имеющими разный приоритет (абсолютный, относительный);
- СМО с заявками, имеющими одинаковый приоритет.
При поступлении в СМО нескольких типов заявок могут быть организованы отдельные очереди для заявок каждого типа. Кроме размера, для каждой такой очереди обычно указывается приоритет находящихся в ней заявок. Приоритеты обычно кодирует целыми числами 0,1,2,3,..., причем, чем меньше число, тем меньше приоритет соответствующих заявок. При наличия приоритетной организации в СМО на обслуживание в первую очередь выбираются заявки с высшими приоритетами. Различают относительный и абсолютный приоритет.
Если заявка с абсолютным приоритетом поступила в CMО в тот момент, когда на обслуживании находятся заявка о меньшим приоритетом, то поступившая заявка сразу начинает обслуживаться, прерывая на время своего обслуживания находящуюся там заявку. Вытесненная таким образом заявка возвращается в начало своей очереди и ожидает продолжение обслуживания (дообслуживания). Для заявок с относительным приоритетом их приоритет вступает в действие не в момент их поступления в СМО, а в момент выбора следующей заявки из очереди (из очередей) на обслуживание. Прерываний в этом случае нет.
Приоритеты заявок бывают статические (постоянные) и динамические (изменяющиеся во времени). В самом общем виде задают дисциплину обслуживания заявок, представляющую собой комбинацию дисциплин со статической я динамической фиксацией приоритетов. Для этого функцию приоритетности задают в виде
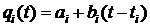
где
- статическая составляющая приоритета заявки с номером i в СМО,
- коэффициент динамической составляющей приоритета,
- момент поступления в СМО заявки с порядковым номером i,
t - текущий момент времени, рассматриваемый на интервале между моментами входа в CМО и выхода после окончания обслуживания i-ой заявки.
Основные задачи теории систем массового обслуживания заключаются
- в расчете характеристик СМО (например, вероятность отказа в обслуживании, среднее число заявок в системе, среднее число занятых каналов и т. д.);
- оценке эффективности СМО на основе рассчитанных характеристик;
- оптимизации параметров СМО.
10.2. Системы массового обслуживания, в которых протекает Марковский случайный процесс «гибели и размножения»
10.2.1. Основные типы систем, соответствующие процессу «гибели и размножения»
Ниже приведены основные типы систем, соответствующие процессу «гибели и размножения», и формулы для расчета основных характеристик.
1. Многоканальные системы без потерь с неограниченным ожиданием и бесконечным потоком требований на входе (разомкнутые системы):
 |
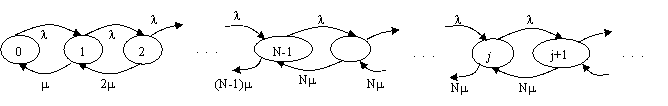μ – интенсивность потока обслуживания;
λ – интенсивность входного потока;
N – число каналов обслуживания;
2. Многоканальные системы с отказами и бесконечным потоком требований на входе (разомкнутые системы):
 |
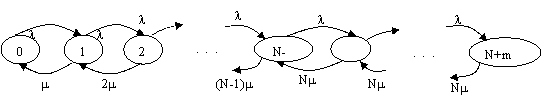Граф динамики многоканальной системы такого вида остается таким же, как и на рис. 1, только количество состояний в графе конечно и равно N+m+1, включая нулевое состояние, где m – величина, ограничивающая длину очереди (в другой терминологии – m – количество мест в накопителе очереди).
3.
Многоканальные системы без потерь с источником конечного числа требований (замкнутые системы):
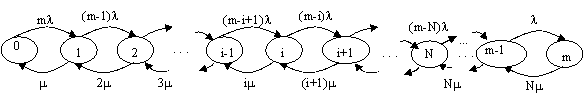
m – максимальное число заявок в СМО, число состояний СМО – m+1, включая нулевое состояние.
10.2.2. Расчет характеристик СМО на основе использования аналитического метода
1. Расчет многоканальных систем без потерь с неограниченным ожиданием и бесконечным потоком требований на входе (разомкнутые системы)
Для нахождения предельных вероятностей состояний составляется система уравнений Колмогорова. Ниже приведены конечные формулы для расчета вероятностей состояний, выведенные из системы уравнений Колмогорова.
,
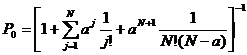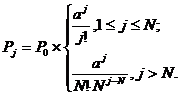
вероятность загрузки системы:
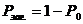
вероятность отказа в обслуживании:
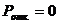, т. к. любая заявка будет рано или поздно обслужена.
среднее число требований в очереди:
, 
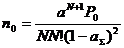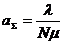
среднее время ожидания в очереди:
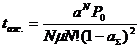
среднее число занятых каналов:
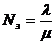
среднее число заявок в системе:
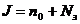, т. е. среднее число заявок в очереди плюс среднее число занятых каналов;
среднее время пребывания требования в системе:
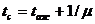, т. е. среднее время ожидания в очереди плюс среднее время обслуживания.
2. Расчет многоканальных систем с отказами и бесконечным потоком требований на входе (разомкнутые системы)
Для нахождения предельных вероятностей состояний составляется система уравнений Колмогорова. Ниже приведены конечные формулы для расчета вероятностей состояний, выведенные из системы уравнений Колмогорова.
, ,
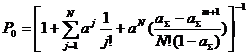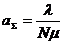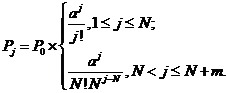
вероятность загрузки системы:
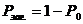
вероятность отказа в обслуживании:
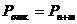, в случае если заняты все каналы и все места в очереди заявка получает отказ.
среднее число требований в очереди:
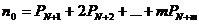
среднее время ожидания в очереди:
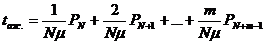
среднее число занятых каналов:
)
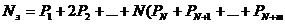среднее число заявок в системе:
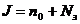, т. е. среднее число заявок в очереди плюс среднее число занятых каналов;
среднее время пребывания требования в системе:
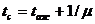, т. е. среднее время ожидания в очереди плюс среднее время обслуживания.
3. Расчет многоканальных систем без потерь с источником конечного числа требований (замкнутые системы)
Для нахождения предельных вероятностей состояний составляется система уравнений Колмогорова. Ниже приведены конечные формулы для расчета вероятностей состояний, выведенные из системы уравнений Колмогорова.
,
|
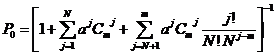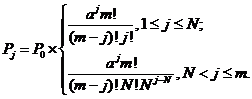
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 |
