Основные определения и понятия теории моделирования, области использования (стр. 2 )

Рис. 4. Структурная схема дифференцирующего фильтра

В уравнении:

K - коэффициент усиления;

х(t) – входной сигнал.

Доказано, что: 

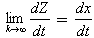
Преобразуем математическую модель фильтра к виду, позволяющему применить принцип t. В простейшем случае достаточно уравнение (1) аппроксимировать конечно-разностным уравнением:

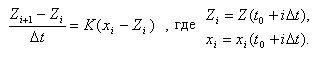
Это соответствует итерационной формуле:

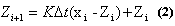
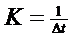(3).

Задав начальное условие Z(t0)=Z0 можно построить траекторию процесса, происходящего в фильтре, с целью получения текущего значения производной любой детерминированной функции x(t), подаваемой на вход.

Пример. Пусть шаг =0,01; x(t)=sin(t)+cos(t); Z(0)=0,5; N=1000.

В табл. 1 приведены результаты вычислений. Порядок вычислений следующий.

1. Зададим моменты времени t, в которые вычисляются значения производной (второй столбец в табл. 1).

2. Вычислим: К=1/=100.

3. Вычислим значения входного сигнала в моменты t: х(t)= sin(t)+cos(t) (третий столбец табл. 1).

4. Вычислим : вычисляется по формуле 2, так как =1, то после преобразования формула 2 имеет вид: ; =0,5 (см. табл. 1).

5. Вычислим 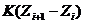- значения производной в моменты времени t на основе имитационного метода (пятый столбец табл. 1).

6. Вычислим значения производной в моменты времени t на основе аналитического метода по формуле: x’(t)=cos(t)-sin(t) (шестой столбец табл. 1).

7. Построим линейный график траекторий изучаемых процессов. На рис. 5 приведены графики исходной функции x(t) и производных x’(t), рассчитанных имитационным методом и аналитическим.

При построении графика не учитывается первая строка табл. 1, так как значение производной, вычисленной имитационным методом, в момент времени 0 соответствует переходному процессу в дифференцирующем фильтре и поэтому значительно отличается от значения производной, вычисленной аналитически. Продолжительность переходного процесса в фильтре зависит от задания начального значения . В данном случае переходный процесс продолжается один временной такт.

Произвести все расчеты и построить линейный график траекторий изучаемых процессов можно средствами MS Excel.

Таблица 1.

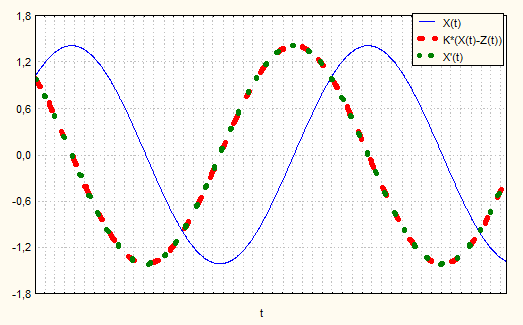
Рис. 5. Графики траекторий изучаемых процессов: исходной функции x(t) и производных x’(t), рассчитанных имитационным методом и аналитическим

Визуальный анализ графика (рис. 5) позволяет сделать вывод о статистической близости результатов, полученных при вычислении производной аналитическим и имитационным методами.

6.4. Пример использования принципа особых состояний при моделировании системы

Пусть рассматриваемая система – библиотека, в которой работает один библиотекарь. Задан интервал прихода между читателями (равномерный 2-6). Задан интервал обслуживания (равномерный 3-4). Реализовать моделирование работы библиотеки по обслуживанию 100 читателей. Рассчитать среднее время ожидания в очереди и вероятность простоя библиотекаря.

1 шаг. Выберем входные, промежуточные и выходные переменные

входные и промежуточные переменные:

Т инт. прих. – интервал между приходом читателей;

Т инт. обс. – интервал облуживания читателя

Т прих. – момент прихода очередного читателя;

Т нач. обс. – момент начала обслуживания очередного читателя;

Т ок. обс. – момент окончания обслуживания очередного читателя;

выходные переменные:

Т ож. – время ожидания читателя в очереди;

Т простоя – время простоя библиотекаря до прихода очередного читателя;

Т ож. ср. – среднее время ожидания читателя в очереди;

Т простоя – суммарное время простоя библиотекаря;

Р простоя – вероятность простоя библиотекаря.

В табл. 2. и рис. 6 приведены данные ручного моделирования обслуживания первых четырех читателей для иллюстрации принципа особых состояний моделирования системы. Интервалы прихода читателей и интервалы обслуживания заданы произвольно.

Таблица 2. Имитационное моделирование обслуживания читателей

Рис. 6.

2 шаг. Разработка блок-схемы алгоритма имитации СМО (рис. 7)

3 шаг. В соответствии с разработанной блок-схемой составляется программа имитации работы СМО на любом языке программирования с использованием любых программных средств.

4 шаг. Расчет показателей эффективности СМО с помощью разработанной программы имитации.

5 шаг. Анализ полученных результатов, оценка эффективности СМО.

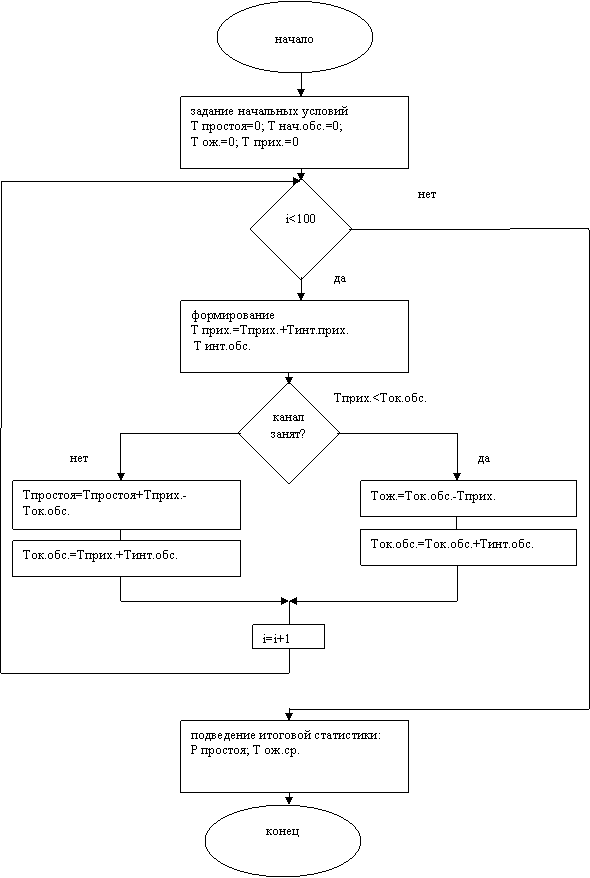
Рис. 7. Блок-схема алгоритма имитации работы СМО

7. Математические основы имитационного моделирования

7.1. Методы генерации случайных чисел

Существует три способа генерации случайных чисел:

1.  Аппаратный - в основе лежит какой-либо физический эффект (например, шумы в электронных устройствах, случайные числа вырабатываются с помощью специального датчика. Этот способ не гарантирует качество последовательности случайных чисел непосредственно во время моделирования. С помощью этого способа нельзя получать одинаковые последовательности. Используется редко.

2.  Табличные - случайные числа оформлены в виде таблицы в оперативной памяти или на внешнем носителе. При этом способе запас чисел ограничен, вычислительные ресурсы используются неэффективно. Используется редко.

3.  Программный (алгоритмический) - случайные числа формируются с помощью специальных программ. Каждое случайное число вычисляется с помощью соответствующей программы по мере возникновения потребностей при моделировании системы на ЭВМ. Этот способ наиболее распространен.

Программная имитация случайных воздействий сводится к генерированию некоторых стандартных (базовых) процессов и к их последующему функциональному преобразованию. Чаще всего в качестве базовой последовательности используют независимые случайные величины, равномерно распределенные на интервале (0,1).

Непрерывная случайная величина имеет равномерное распределение в интервале (a, b), если ее функции плотности и распределения соответственно примут вид

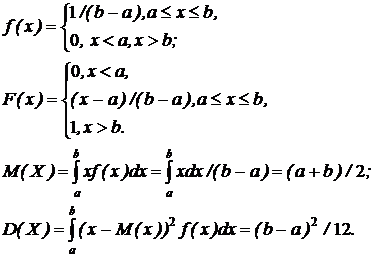
Для получения случайных чисел на ЭВМ используются алгоритмы, поэтому такие последовтельности, являющиеся по сути детерминированными, называются псевдослучайными. ЭВМ оперирует n-разрядными числами, поэтому поэтому на ЭВМ вместо непрерывной совокупности равномерных случайных чисел интервала (0,1) используют дискретную последовательность 2n случайных чисел того же интервала - закон распределения такой дискретной последовательности называется квазиравномерны распределением.

Требования к идеальному генератору случайных чисел:

1.  Последовательность должна состоять из квазиравномернло распределенных чисел.

2.  Числа должны быть независимыми.

3.  Последовательности случайных чисел должны быть воспроизводимыми.

4.  Последовательности должны иметь неповторяющиеся числа.

5.  Последовательности должны получаться с минимальными затратами вычислительных ресурсов.

Наибольшее применение в практике моделирования на ЭВМ для генерации последовательностей псевдослучайных числе находят алгоритмы вида:

xi+1=Ф(xi),

представляющие собой реккурентные соотношения первого порядка.

Одна из первых процедур исторически сложившихся – метод серединных квадратов.

Пример. x0 = 0,2152 , (x0)2=0, , x1 = 0,6311 , (x1)2=0,, x2=0,8287 и т. д. Пусть имеется 2n-разрядное число меньше 1, возведем его в квадрат, а затем отберем средние 2n разрядов.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5