Недостаток подобных методов - наличие корреляции между числами последовательности, а иногда случайность вообще отсутствует, например:
x0 = 0,4500 , (x0)2=0,, x1 = 0,2500 , (x1)2=0,, x2=0,2500 и т. д.
Широкое применение получили конгруэнтные процедуры генерации псевдослучайных последовательностей.
В основе лежит понятие конгруэнтности. Два целых числа a и b конгруэнтны (сравнимы) по модулю m, где m - целое число, тогда и только тогда, когда существует такое целое число k, что a-b=km, т. е. если разность делится на m и если числа a и b дают одинаковые остатки от деления на абсолютную величину числа m.
Пример: a=9375 и b=1875: =7500=4*1875
=2500=4*625.
Большинство конгруэнтных процедур генерации случайных чисел основаны на следующей формуле:
![]()
где 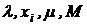 - неотрицательные целые числа.
- неотрицательные целые числа.
По целым числам последовательности {Xi} можно построить последовательность {xi}={Xi/M} рациональных чисел из единичного интервала (0,1).
Конгруэнтная процедура получения последовательности псевдослучайных чисел квазиравномерно распределенных чисел может быть реализована мультипликативным или смешанным методом.
Мультипликативный метод.
Задает последовательность неотрицательных целых чисел {Xi} не превосходящих М по формуле:
![]() ,
,
где 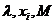 - неотрицательные целые числа.
- неотрицательные целые числа.
Выражение означает: равен остатку от деления на M.
В силу детерминированности метода получают воспроизводимые последовательности.
В качестве X0 выбирают произвольное нечетное число; М – число определяющее, наибольшее значение получаемых случайных чисел, при машинной реализации ![]() , р – основание системы счисления, g – число бит в машинном слове.
, р – основание системы счисления, g – число бит в машинном слове.
Смешанный метод.
Задает последовательность неотрицательных целых чисел {Xi} не превосходящих М по формуле:
![]() ,
,
где 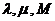 - неотрицательные целые числа.
- неотрицательные целые числа.
С вычислительной точки зрения метод сложнее, но введение дополнительного параметра позволяет уменьшить возможную корреляцию между генерируемыми числами.
В настоящее время почти все библиотеки стандартных программ для вычисления последовательностей равномерно распределенных СЧ основаны на конгруэнтной процедуре.
Применяемые генераторы случайных чисел перед моделированием должны пройти тщательное предварительное тестирование на равномерность, стохастичность и независимость получаемых последовательностей случайных чисел.
Методы улучшения качества последовательностей случайных чисел:
Один из методов: использование рекуррентных формул порядка r:
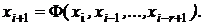
Но применение этого способа приводит к увеличению затрат вычислительных ресурсов на получение чисел.
7.2. Методы имитационного моделирования случайных величин
Моделирование непрерывной случайной величины. Метод обратной функции
Для получения непрерывных случайных величин с заданным законом распределения, как и для дискретных величин, можно воспользоваться методом обратной функции. Если случайная величина Y имеет плотность распределения f(y), то распределение случайной величины
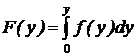
является равномерным на интервале (0,1). Чтобы получить число, принадлежащее последовательности случайных чисел {yi}, имеющих функцию плотности f(y), необходимо разрешить относительно yi уравнение
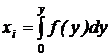
где xi - число, принадлежащее последовательности случайных чисел равномерно распределенных на интервале от (0,1).
Пример. Необходимо получить случайные числа с показательным (экспоненциальным) законом распределения (например, интервалов времени между поступлениями заявок на обслуживание):
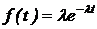 .
.
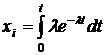
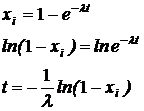
![]() - случайное число, имеющее равномерное распределение на интервале (0,1). Тогда
- случайное число, имеющее равномерное распределение на интервале (0,1). Тогда
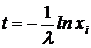
Этот способ получения случайных чисел с заданным законом распределения имеет ограниченную сферу применения, так как для многих законов распределения, встречающихся в практических задачах моделирования, интеграл не берется, т. е. приходится прибегать к численным методам решения, что увеличивает затраты вычислительных ресурсов на получение каждого числа; даже для случаев, когда интеграл берется в конечном виде получаются формулы, содержащие действия логарифмирования, извлечения корня и т. д., что также резко увеличивает затраты машинного времени на получение каждого случайного числа. Поэтому на практике часто пользуются приближенными способами преобразования случайных чисел, которые можно классифицировать следующим образом:
а) универсальные способы, с помощью которых можно получать случайные числа с законом распределения любого вида; б) неуниверсальные способы, пригодные для получения случайных чисел с конкретным законом распределения.
Метод, основанный на кусочной аппроксимации функции плотности распределения. Рассмотрим приближенный универсальный способ получения случайных чисел, основанный на кусочной аппроксимации функции плотности.
Пусть требуется получить последовательность случайных чисел {yj} с функцией плотности fh(y) , значения которой лежат в интервале (a, b). Разобъем интервал (a, b) на m интервалов (рис. 8), и будем считать fh(y) на каждом интервале постоянной. Разбивать необходимо так, чтобы вероятность попадания случайной величины в любой интервал (ak, ak+1) была постоянной, т. е.:
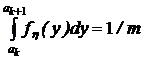
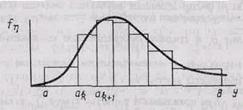
Рис. 8. Кусочная аппроксимация функции плотности
В таком случае, алгоритм этого способа получения случайных чисел сводится к выполнению следующих действий:
1) Генерируется случайное равномерно распределенной число xi из интервала (0,1);
2) с помощью этого числа выбирается интервал (ak, ak+1);
3) генерируется число xi+1 ;
4) вычисляется случайное число yj =ak+ xi+1(ak+1-ak) с требуемым законом распределения.
Рассмотрим пример применения способа преобразования последовательности равномерно распределенных случайных чисел {xi} в последовательность с заданным законом распределения {yi} на основе предельных теорем теории вероятностей. Такие способы ориентированы на получение последовательностей чисел с конкретным законом распределения, т. е. не являются универсальными.
Приближенный метод генерации последовательности значений нормально распределенной СВ. Пусть требуется получить последовательность случайных чисел {yi}, имеющих нормальное распределение с математическим ожиданием m и средним квадратическим отклонением s:
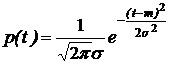
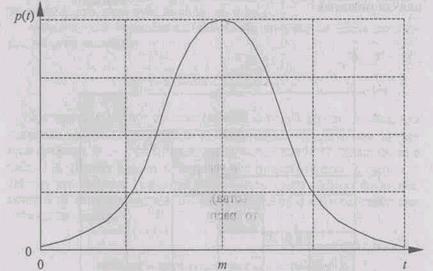
Рис. 9. Вид нормального распределения
Будем формировать случайные числа tj в виде сумм последовательностей случайных чисел {xi}, равномерно распределенных на интервале от (0,1). Можно воспользоваться центральной предельной теоремой: Если X1 , X2,..., Xn - независимые одинаково распределенные случайные величины, имеющие математическое ожидание M(Xi)=a и дисперсию s2, то при N ® ¥ сумма ![]() асимптотически нормальна с математическим ожиданием Na и средним квадратическим отклонением
асимптотически нормальна с математическим ожиданием Na и средним квадратическим отклонением ![]() . Практически достаточно N=8¸12, а в простейших случаях - 4¸5. Преимущество этого способа - высокое быстродействие. Недостатком является игнорирование «хвостов» нормального распределения, которые могут уходить в обе стороны от величины т на расстояние, превышающее 6s. Поэтому при проведении особо точных экспериментов применяются другие - более точные (но более медленные) способы. В современных системах имитационного моделирования обычно используются не менее двух программных датчиков случайных величин, распределенных по нормальному закону (их выбор осуществляется автоматически управляющей программой).
. Практически достаточно N=8¸12, а в простейших случаях - 4¸5. Преимущество этого способа - высокое быстродействие. Недостатком является игнорирование «хвостов» нормального распределения, которые могут уходить в обе стороны от величины т на расстояние, превышающее 6s. Поэтому при проведении особо точных экспериментов применяются другие - более точные (но более медленные) способы. В современных системах имитационного моделирования обычно используются не менее двух программных датчиков случайных величин, распределенных по нормальному закону (их выбор осуществляется автоматически управляющей программой).
Метод Неймана. Метод Неймана является универсальным. Единственным ограничением его применения является то, что СВ должна задаваться усеченным законом, или законом, который может быть аппроксимирован усеченным.

Рис. 10.
На рис. 10 изображено ![]() - функция плотности распределения случайной величины
- функция плотности распределения случайной величины ![]() , заданная на интервале
, заданная на интервале ![]() . Максимальное значение функции
. Максимальное значение функции ![]() обозначено W.
обозначено W.
Метод состоит в следующем:
1. С помощью датчика случайных чисел, равномерно распределенных на интервале (0,1), выбирают пары чисел ![]() . (точка
. (точка ![]() на рис. 4).
на рис. 4).
2. Формируется преобразованная пара чисел, равномерно распределенных на интервале соответственно ![]() и
и ![]() :
:
![]()
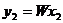
Проверяется выполнение неравенства
![]()
Если оно выполнено, то ![]() и есть искомое значение случайной величины
и есть искомое значение случайной величины ![]() . На рис. 10 это соответствует первой координате точки
. На рис. 10 это соответствует первой координате точки ![]() . В противном случае вновь генерируются случайные числа и алгоритм повторяется заново.
. В противном случае вновь генерируются случайные числа и алгоритм повторяется заново.
7.3. Имитационное моделирование случайных событий
Имитация элементарного события. Необходимо реализовать случайное событие А, наступающее с заданной вероятностью p. Определим А как событие, состоящее в том, что выбранное значение xi равномерно распределенной на интервале (0,1) случайной величины удовлетворяет неравенству:
xi =<p.
Тогда вероятность события А будет 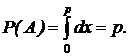 Противоположное событие состоит в том, что xi >p, его вероятность равна 1-р.
Противоположное событие состоит в том, что xi >p, его вероятность равна 1-р.
Имитация полной группы событий. Рассмотрим группу событий. Пусть А1, А2 ,..., Аs - полная группа событий, наступающих с вероятностями p1, p2 ,..., ps соответственно. Определим событие Аm как событие, состоящее в том, что выбранное значение xi случайной величины удовлетворяет неравенству
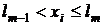 ,
,
где 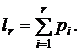
Процедура моделирования испытаний в этом случае состоит в последовательном сравнении случайных чисел xi со значениями lr. Если условие выполняется, исходом испытания оказывается событие Аm.
Описанный алгоритм иногда называют алгоритмом «розыгрыша по жребию».
Имитация сложного события, состоящего, например, из двух независимых элементарных событий А и В заключается в проверке неравенств: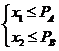
Здесь ![]() и
и ![]() - СЧ с равномерным законом распределения, принадлежащие интервалу (0, 1).
- СЧ с равномерным законом распределения, принадлежащие интервалу (0, 1).
В зависимости от исхода проверки неравенств делается вывод, какой из вариантов сложного события: ![]() имеет место.
имеет место.
Имитация зависимых событий. В случае, когда сложное событие состоит из элементарных зависимых событий А и В имитация сложного события производится с помощью проверки следующих неравенств: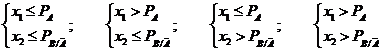 .
.
В зависимости от того, какая из этих четырех систем неравенств выполняется, делается вывод о том, какой из четырех возможных исходов имеет место: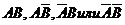 .
.
В качестве исходных данных задаются ![]() . Условная вероятность может быть вычислена по формуле полной вероятности. Алгоритм модели подобного случая может быть следующим:
. Условная вероятность может быть вычислена по формуле полной вероятности. Алгоритм модели подобного случая может быть следующим:
1. Генерируется значение ![]() .
.
2. Проверяется условие ![]() . Если условие выполняется, то считается, что событие А произошло и счетчик событий увеличивается на 1: КА=КА+1. Если условие не выполняется, то событие А не произошло и соответствующий счетчик увеличивается на 1: КNА=КNА+1.
. Если условие выполняется, то считается, что событие А произошло и счетчик событий увеличивается на 1: КА=КА+1. Если условие не выполняется, то событие А не произошло и соответствующий счетчик увеличивается на 1: КNА=КNА+1.
3. Генерируется значение ![]() .
.
4. Проверяется условие ![]() . Если условие выполняется, то считается, что событие В произошло и на 1 увеличивается один из счетчиков: либо КАВ=КАВ+1 (если событие А имело место); либо КNАВ=КNАВ+1 (если событие А не произошло). Если условие не выполняется, то событие В не произошло и один из счетчиков увеличивается на 1: либо КАNВ=КАNВ+1 (если событие А имело место); либо КNАNВ=КNАNВ+1 (если событие А не произошло).
. Если условие выполняется, то считается, что событие В произошло и на 1 увеличивается один из счетчиков: либо КАВ=КАВ+1 (если событие А имело место); либо КNАВ=КNАВ+1 (если событие А не произошло). Если условие не выполняется, то событие В не произошло и один из счетчиков увеличивается на 1: либо КАNВ=КАNВ+1 (если событие А имело место); либо КNАNВ=КNАNВ+1 (если событие А не произошло).
5. Рассчитывается вероятность наступления исходов![]() , как отношение значения соответствующего счетчика к общему количеству испытаний:
, как отношение значения соответствующего счетчика к общему количеству испытаний:
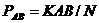 ,
,
где N – общее число испытаний.
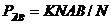 .
.
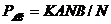 .
.
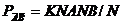 .
.
Блок-схема метода приведена на рис. 11.
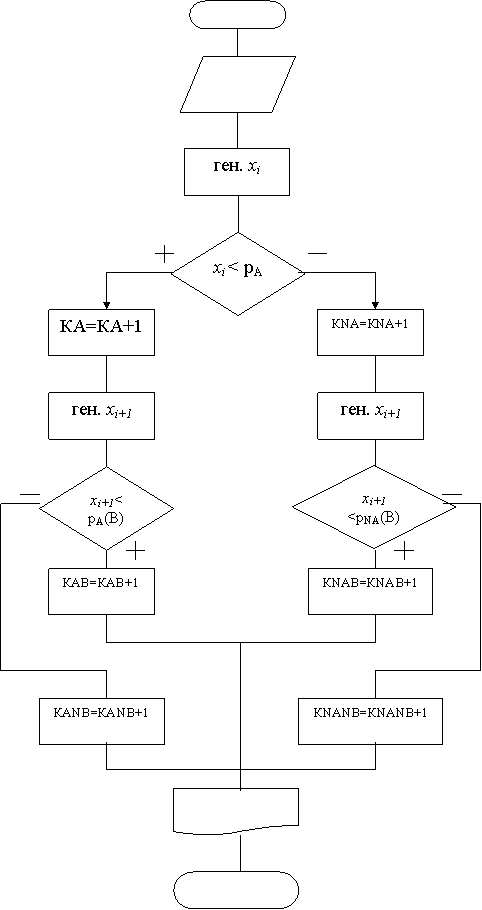

Рис. 11. Блок-схема алгоритма имитации зависимых событий
8. Статистическое моделирование
8.1. Метод статистического моделирования
Метод статистического моделирования на ЭВМ - основной метод получения результатов с помощью имитационных моделей стохастических систем, использующий в качестве теоретической базы предельные теоремы теории вероятностей.
Основа - метод статистических испытаний Монте-Карло, который базируется на использовании случайных чисел, то есть возможных значений некоторой случайной величины с заданным распределением вероятностей. Статистическое моделирование представляет собой метод получения с помощью ЭВМ статистических данных о процессах, происходящих в моделируемой системе.
Сущность метода: построение для процесса функционирования исследуемой системы S некоторого моделирующего алгоритма (программы имитации), имитирующего поведение и взаимодействие элементов системы с учетом случайных входных воздействий и воздействий внешней среды и реализации этого алгоритма с использованием программно-технических средств ЭВМ.
Области применения: 1) изучение стохастических систем; 2) решение детерминированных задач.
Результат статистического моделирования - серия частных значений искомых величин или функций, их статистическая обработка. Если количество реализаций N ® ¥, результаты устойчивы и достаточно точны.
Теоретическая основа метода статистического моделирования являются пре дельнее теоремы теории вероятностей. Их значение - гарантируют высокое качество статистических оценок при числе испытаний N ® ¥. Часто приемлемые результаты могут быть получены при достаточно небольших N.
Неравенство Чебышева. Для неотрицательной случайной величины X и любого K>0 выполняется неравенство:
P(X>=K)=<M(X)/K
Теорема Бернулли. Если проводится N независимых испытаний, в каждом из которых некоторое событие А осуществляется с вероятностью p, то относительная частота появления события m/N при N ® ¥ сходится по вероятности к p, т. е. при любом e>0
![]() , где m - число положительных исходов испытания.
, где m - число положительных исходов испытания.
Теорема Пуассона.
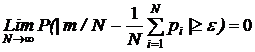 , где pi - вероятность осуществления события А в i-м испытании.
, где pi - вероятность осуществления события А в i-м испытании.
Обобщенная теорема Чебышева.
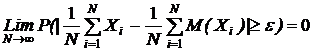 , Xi - i-ая случайная величина
, Xi - i-ая случайная величина
Теорема Маркова. Обобщенная теорема Чебышева справедлива и для зависимых случайных величин, если
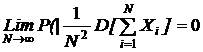
Центральная предельная теорема. Если X1 , X2,..., Xn - независимые одинаково распределенные случайные величины, имеющие математическое ожидание M(Xi)=a и дисперсию s2, то при N ® ¥ закон распределения суммы 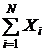 неограниченно приближается к нормальному:
неограниченно приближается к нормальному:
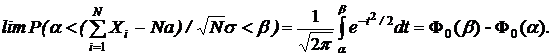
Приведем пример применения методов статистического моделирования.
Пример. Проводится s=10 независимых выстрелов по мишени, причем вероятность попадания при одном выстреле задана и равна p. Требуется оценить вероятность того, что число попаданий в мишень будет четным.
Аналитическое решение этой задачи:
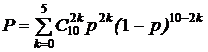
Схема алгоритма (статистическое моделирование) (рис. 12):
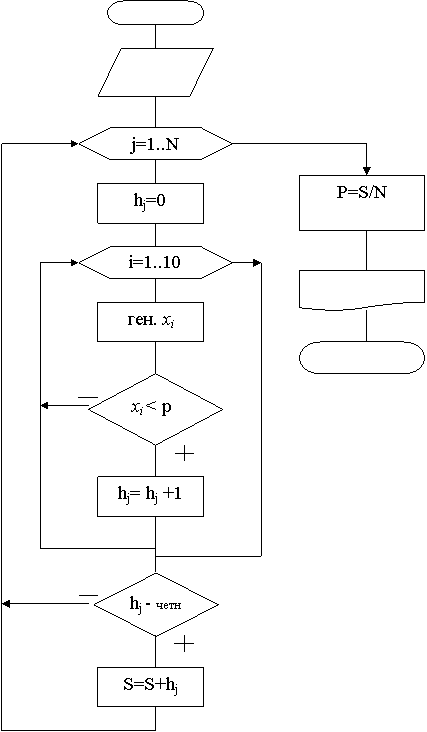

Рис. 12.
8.2. Обработка результатов моделирования
В процессе имитационного моделирования формируется большое количество реализаций, являющихся исходным статистическим материалом для нахождения приближенных значений показателей эффективности или, как говорят, их оценок.
Оценкой вероятности является частота ![]() . Для ее получения обычно организуют на программном уровне 2 счетчика: один для подсчета общего количества экспериментов N, второй – для подсчета количества положительных исходов n.
. Для ее получения обычно организуют на программном уровне 2 счетчика: один для подсчета общего количества экспериментов N, второй – для подсчета количества положительных исходов n.
В качестве характеристик исследуемой системы выступает закон плотности распределения. Его приближенно можно охарактеризовать гистограммой. Для этого интервал измерения СВ разбивают на отрезки ![]() , каждому из них сопоставляют счетчик, где накапливают
, каждому из них сопоставляют счетчик, где накапливают ![]() - количество попаданий значений СВ в
- количество попаданий значений СВ в ![]() . На каждом
. На каждом ![]() строится прямоугольник с высотой
строится прямоугольник с высотой ![]() . Полученную гистограмму можно сгладить.
. Полученную гистограмму можно сгладить.
Оценку математического ожидания получают как среднее арифметическое значение yi СВ
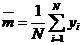
Оценку дисперсии можно вычислять по формуле
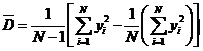
Определение объема выборки.
Объем выборки – это количество реализаций, которое необходимо при имитационном моделировании, чтобы обеспечить стохастическую точность результата.
При вычислении оценки математического ожидания с заданной точностью и достоверностью объем выборки можно вычислить по формуле:
![]()
Здесь: ![]() - квантиль нормального распределения вероятностей порядка
- квантиль нормального распределения вероятностей порядка
![]() ;
;
![]() - уровень достоверности;
- уровень достоверности;
![]() - заданная погрешность, с которой необходимо получить оценку математического ожидания.
- заданная погрешность, с которой необходимо получить оценку математического ожидания.
Здесь ![]() - центральный момент четвертого порядка случайно величины.
- центральный момент четвертого порядка случайно величины.
Количество реализаций для получения оценки ![]() с заданной точностью
с заданной точностью ![]() можно вычислить по формуле:
можно вычислить по формуле:
![]()
Здесь ![]() - центральный момент четвертого порядка СВ
- центральный момент четвертого порядка СВ
![]() - среднеквадратическое отклонение:
- среднеквадратическое отклонение: 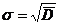 .
.
Как видно из приведенных формул (2) – (5), для их практического использования необходимо знать 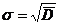 и
и ![]() , которые как правило бывают неизвестными. В этом случае используют вместо точных значений
, которые как правило бывают неизвестными. В этом случае используют вместо точных значений ![]() и
и ![]() их оценки, получаемые предварительно при некотором N. Если при этом заданная точность
их оценки, получаемые предварительно при некотором N. Если при этом заданная точность ![]() не достигнута, то N увеличивают, после чего проводится уточнение оценок. Этот процесс повторяется до тех пор, пока заданная точность будет обеспечена.
не достигнута, то N увеличивают, после чего проводится уточнение оценок. Этот процесс повторяется до тех пор, пока заданная точность будет обеспечена.
Критерий согласия хи-квадрат (Пирсона).
При обработке результатов машинного эксперимента с моделью системы часто возникает задача определения эмпирического закона распределения случайной величины. Общая схема решения этой задачи сводится к тому, что:
· строят по результатам имитационного эксперимента гистограмму (оценку функции плотности распределения вероятностей);
· выдвигают гипотезу о согласии эмпирического закона с каким-либо теоретическим распределением;
· проверяют гипотезу с помощью одного из статистических критериев согласия (Пирсона, Колмогорова, Смирнова и т. д.
В качестве критерия проверки гипотезы по методу Пирсона выбирают величину, которая характеризует степень расхождения эмпирического и теоретического закона следующим образом:
![]()
где: ![]() - количество значений случайной величины
- количество значений случайной величины ![]() , попавших в i – ый подынтервал;
, попавших в i – ый подынтервал;
![]() - вероятность попадания случайно величины
- вероятность попадания случайно величины ![]() в i – ый подынтервал;
в i – ый подынтервал;
d- количество подынтервалов, на которые разбивается интервал измерения в имитационном эксперименте.
![]() - объем наблюдений.
- объем наблюдений.
При 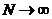 закон распределения величины хи-квадрат, являющейся мерой расхождения, зависит только от количества подынтервалов и приближается к закону распределения
закон распределения величины хи-квадрат, являющейся мерой расхождения, зависит только от количества подынтервалов и приближается к закону распределения ![]()
![]()
![]() с
с 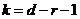
![]() степенями свободы, где
степенями свободы, где ![]() - число параметров теоретического закона распределения. Функция распределения
- число параметров теоретического закона распределения. Функция распределения ![]() величины
величины ![]() табулирована
табулирована
Проверка гипотезы о согласованности эмпирического и теоретического законов распределения с помощью критерия согласия Пирсона осуществляется в последовательности:
1. Результаты наблюдений ![]() группируют в интервальный вариационный ряд. Объем наблюдений должен быть достаточно большим (
группируют в интервальный вариационный ряд. Объем наблюдений должен быть достаточно большим (![]() ). Если частота, соответствующая какому-либо интервалу, окажется меньше 5, то интервал объединяют с соседним, так, чтобы частота попадания значения случайной величины в подынтервал была бы больше или равна 5.
). Если частота, соответствующая какому-либо интервалу, окажется меньше 5, то интервал объединяют с соседним, так, чтобы частота попадания значения случайной величины в подынтервал была бы больше или равна 5.
2. Выдвигают гипотезу о виде распределения по виду гистограммы.
3. Задают уровень значимости ![]() .
.
4. Определяют теоретическую вероятность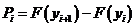 попадания случайно величины
попадания случайно величины ![]() в каждый из подинтервалов.
в каждый из подинтервалов.
5. Вычисляют величину расхождения законов![]() .
.
6. Определяют число степеней свободы ![]() .
.
7. По вычисленным значениям ![]() и
и ![]() по таблицам находят вероятность
по таблицам находят вероятность![]() . Если она превышает уровень значимости
. Если она превышает уровень значимости ![]() , то считают, что гипотеза о виде распределения отвергается.
, то считают, что гипотеза о виде распределения отвергается.
9. Элементы теории Марковских случайных процессов, используемые при моделировании систем
9.1. Потоки событий
Одним из важных понятий, используемых при моделировании систем является понятие потока событий, который поступает на вход системы.
Математическая модель потока событий
Потоком событий называется последовательность однородных событий, появляющихся одно за другим в случайные моменты времени. Примеры: поток вызовов на телефонной станции, поток автомашин, подъезжающих на заправочную станцию, поток заболеваний гриппом в зимний сезон, поток забитых шайб при игре в хоккей, поток заявок на ремонт, поступающих в ремонтную организацию, поток отказов (сбоев) ЭВМ в ходе ее работы, поток электронов, вылетающих с катода радиолампы, поток электрических импульсов, поступающих от мозга в мышцу для ее возбуждения, и т..
События, образующие поток, в общем случае могут быть и неоднородными, например если в потоке автомашин, прибывающих на заправку, различать легковые и грузовые.
Математическое представление потока событий. “Поток событий” представляет собой в общем случае просто последовательность случайных точек q1, q2,…, qn,… на оси времени 0t с разделяющими их случайными интервалами T1,T2,…,Tn-1,Tn,…, так что
T1=q2-q1, T2=q3-q2,…, Tn=qn+1-qn
 0 q1 q2 q3 qn-1 qn qn+1 t
0 q1 q2 q3 qn-1 qn qn+1 t
Потоки событий различаются между собой по их внутренней структуре: по законам распределения интервалов T1,T2,… между событиями. Для описания распределения интервалов между событиями могут использоваться различные законы распределения: нормальный, равномерный, экспоненциальный (наиболее часто используемый). Также потоки различаются по их взаимной зависимости или независимости и т. д.
С первого взгляда наиболее простым представляется поток событий, в котором интервалы между событиями строго одинаковы и равны определенной неслучайной величине t (рисунок 3). Такой поток событий называется регулярным. Примеры регулярных потоков представляют собой поток изменений минутной цифры на вокзальных электронных часах, поток изменений состояний ЭВМ, определяемый тактом ее работы и т. п.
Регулярный поток событий довольно редко встречается на практике; он представляет определенный интерес как предельный случай для других потоков. Однако несмотря на свою видимую простоту, регулярный поток не имеет преимуществ при математическом анализе, так как намного уступает по проведения расчетов другим типам потоков.
Математическая модель простейшего пуассоновского потока
На практике чаще всего ограничиваются рассмотрением простейшего (пуассоновского) потока заявок.
Определение. Поток событий, обладающий свойствами ординарности, стационарности и отсутствия последействия, называется простейшим (или стационарным пуассоновским) потоком. Для простейшего потока событий вероятность того, что на участке времени длины t наступит ровно k событий, имеет распределение Пуассона и определяется по формуле
Р{X(t,t) = k} = ake-a/k! (k=0, 1, 2,…)
где, а = lt, l - интенсивность потока.
Физический смысл интенсивности потока событий – это среднее число событий, приходящееся на единицу времени (число заявок в единицу времени), размерность – 1/время.
Простейшим этот поток назван потому, что исследование систем, находящихся под воздействием простейших потоков, проводится самым простым образом.
Распределение интервалов между заявками для простейшего потока будет экспоненциальным (показательным) с функцией распределения 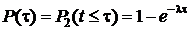 и плотностью
и плотностью ![]() , где
, где ![]() - интенсивность поступления заявок в СМО.
- интенсивность поступления заявок в СМО.
Математическое ожидание длины интервала времени между последовательными моментами поступления событий:
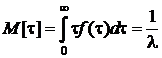
Дисперсия интервала времени между последовательными моментами поступления заявок
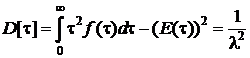
Следовательно, среднеквадратичное отклонение длины интервалов:
![]() .
.
Свойства простейшего пуассоновского потока
ординарность (в каждый момент времени в СМО может поступать не более одной заявки). Ординарность потока означает, что вероятность попадания на элементарный участок Dt двух или более событий пренебрежимо мала по сравнению с вероятностью попадания на него ровно одного события, т. е. при Dt->0 эта вероятность представляет собой бесконечно малую высшего порядка.
![]()
В каждый момент времени в СМО может поступать не более одной заявки
Примерами ординарных потоков событий могут служить поток деталей, поступающих на конвейер для сборки, поток отказов технического устройства, поток автомашин, прибывающих на станцию техобслуживания. Примером неординарного потока может служить поток пассажиров, прибывающих в лифте на данный этаж.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 |




