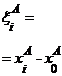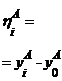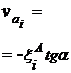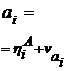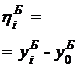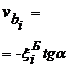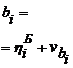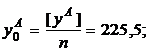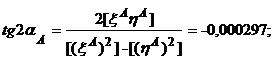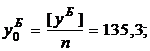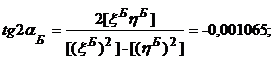По данной методике находят оптимальные оси путей, которые наиболее правильно отражают положение разбивочных (проектных) осей путей; так как находятся с использованием всех измеренных значений пролетов, отклонений от створов и «подгоняются» под средний пролет кранов. Кроме того, производится уравнивание измеренных величин и оценка точности измерений.

Задача нахождения оптимальных осей и отклонений рельсов от них разбивается на ряд этапов:

- нахождение отклонений рельсов от частных оптимальных осей;

- нахождение отклонений рельсов от параллельных оптимальных осей обеих ниток;

- нахождение отклонений рельсов от оптимальных осей, соответствующих среднему пролету кранов;

- уравнивание отклонений;

- оценка точности измерений.

Нахождение отклонений рельсов от частных оптимальных осей

Вероятнейшие отклонения для одной нитки рельсов могут быть найдены по формулам, основанным на составлении и решении условных уравнений или через центральные координаты. Однако более быстрое и простое решение получается при определении тангенса угла между вероятнейшей (искомой) прямой и осью Х (рис. 7.9). При решении поставленной задачи предположим, что одна из переменных величин х измерена с пренебрегаемыми погрешностями, а поэтому необходимо считаться только с погрешностями измерения другой переменной величины y = f(x). Практически почти всегда бывает именно так. Предположим также, что другой аргумент измерен точно через равные промежутки.

Обозначая в случае равноточных измерений

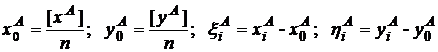, (7.12)

имеем для определения тангенса угла между искомой прямой и осью Х формулу

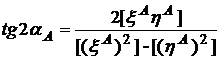. (7.13)

После определения вычисляют сначала поправки

, (7.14)

а затем оптимальные отклонения

. (7.15)

Точно так же находят оптимальные отклонения для второй нитки рельсов (ряд Б) по результатам отклонений от произвольно выбранной съемочной оси.

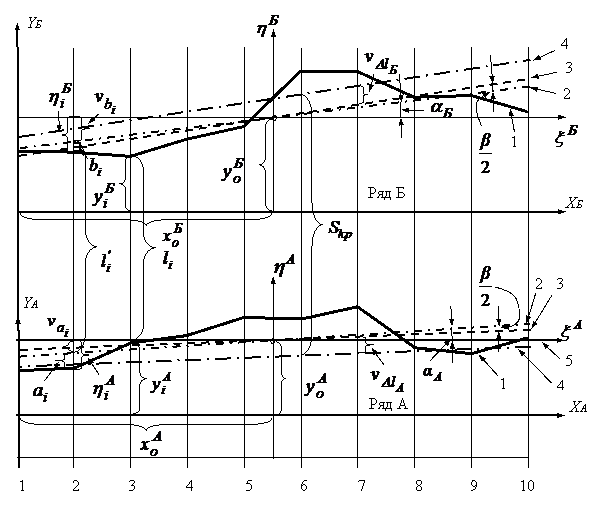
Рис. 7.9. Схема приведения съемочных осей к проектным осям пути
мостового крана по усложненной методике:

1 – положение рельсов; 2 – частная оптимальная ось каждой нитки рельсов; 3 – оптимальные оси двух ниток рельсов; 4 – оптимальные оси рельсов, пригнанные к среднему пролету кранов; 5 – съемочная ось, приведенная к центральным координатам

Нахождение угла между частными оптимальными осями рельсов
и приведение отклонений рельсов к параллельным осям путей

Найденные частные оптимальные оси не будут строго параллельны между собой и составят угол , который находится следующим образом.

По измеренному расстоянию между подкрановыми рельсами на каждом пролете и по частным оптимальным отклонениям (ряда А) и (ряда Б) находят расстояния между частными оптимальными осями на каждом пролете по формуле

(7.16)

Если принять одну из частных оптимальных осей, например , за ось , а расстояние между частными оптимальными осями откладывать по оси , то угол между частными оптимальными осями рядов А и Б определится по формуле

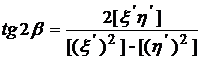, (7.17)

где

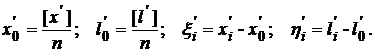(7.18)

После определения , применяя принцип равных влияний, вычисляют сначала поправки за разворот осей

, (7.19)

а затем – оптимальные отклонения от параллельных осей

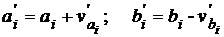. (7.20)

Сдвижка осей до размеров среднего пролета кранов
и расчет отклонений

Расстояние между параллельными осями, равное , не будет точно соответствовать среднему расстоянию между осями колес кранов. При эксплуатации кранов необходимо, чтобы эти расстояния были одинаковыми. Следовательно, оптимальные параллельные оси путей необходимо раздвинуть на отрезки, равные

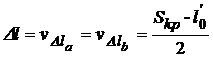, (7.21)

где – средний пролет кранов цеха, а в отклонения 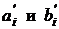ввести поправки

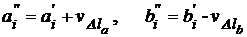. (7.22)

Уравнивание отклонений рельсов

Если бы не было погрешностей измерений, то сумма отклонений обеих ниток рельсов и расстояния между ними в одном поперечном сечении были бы равны расстоянию между искомыми параллельными осями или среднему пролету кранов цеха, т. е.

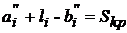. (7.23)

В действительности, из-за погрешностей измерений расстояния между рельсами и отклонений от прямой на обеих нитках рельсов в каждом поперечном сечении путей получим суммарные погрешности

, (7.24)

которые должны быть устранены уравниванием результатов измерений, т. е. введением поправок. Принимая погрешности измерений отклонений по обеим ниткам и ошибки измерений расстояний между ними одинаковыми, в измеренные величины вводим поправки , равные 1/3 суммарной погрешности и противоположные по знаку. Тогда формулы окончательно уравненных отклонений ниток рельсов от оптимальных осей, параллельных между собой и равных среднему пролету кранов, получат следующий вид:

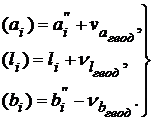(7.25)

Вычисления контролируют по формуле

. (7.26)

На основании формулы (7.24) получаем суммарные погрешности геодезических измерений в каждом поперечном сечении подкрановых путей. Перейдя к средним квадратическим погрешностям, будем иметь

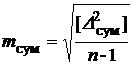. (7.27)

Суммарная погрешность складывается из погрешностей в измерении отклонений по каждой нитке рельсов и погрешности измерения расстояний между нитками. Применяя принцип равных влияний погрешностей измерений, получим среднюю квадратическую погрешность в определении отклонений

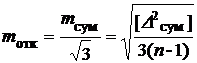. (7.28)

Обработка материалов измерений производится в специальной ведомости (табл. 7.2). Исходными данными служат результаты плановой съемки параметров, приведенные на рис. 7.4. Построение схемы планового положения пути и проект рихтовки выполняют таким же образом, как и при упрощенной обработке измерений.

Из графиков положения путей, обработанных по сложной методике и представленных на рис. 7.10, видно, что взаимное положение рельсов и балок незначительно отличается от графиков положения путей, обработанных по простой методике и представленных на рис. 7.8. Однако, в качестве изменений сомневаться не приходится. При тех же допустимых отклонениях измеряемых параметров объемы рихтовки путей сокращаются в несколько раз. Так как отклонения подсчитаны от оптимальной оси, наиболее близкой к разбивочной, то они более правильно отражают действительное положение конструкций.

Таблица 7.2

Ведомость обработки результатов плановой съемки подкрановых путей
турбинного цеха Главного корпуса ТЭС по усложненной методике
(все размеры даны в мм)

Продолжение табл. 7.2

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5